2D transformation matrices

A matrix can be used to describe or calculate transformations in 2 dimensions.

It can be used to describe any affine transformation. This includes scaling, rotating, translating, skewing, or any combination of those transformations.

Most 2-dimensional transformations can be specified by a simple 2 by 2 square matrix, but for any transformation that includes an element of translation, a 3 by 3 matrix is required.

Applying a matrix transformation

If we have a 2 by 2 matrix:

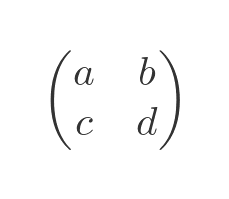
If we multiply this matrix by a column vector we get another column vector:

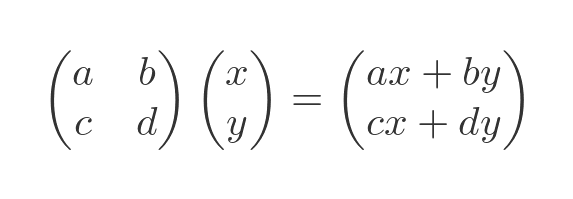
The elements of the new vector are formed from a linear combination of the elements of the original vector.

Notice that, by convention, we multiply the vector by the matrix, rather than the other way round. This is useful when we want to apply a combination of 2 or more transformations. It allows us to multiply the matrices together to create a single transformation matrix.

Scaling transformations

A scaling transformation uses the following matrix:

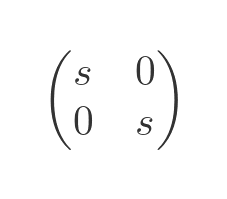
Here is the effect it has on a vector:

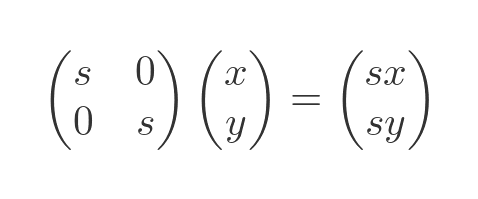
If we take a unit square and apply this transform to each of its vertices, we get the new shape on the right. We have used an s value of 2, which scales the shape by a factor of 2:

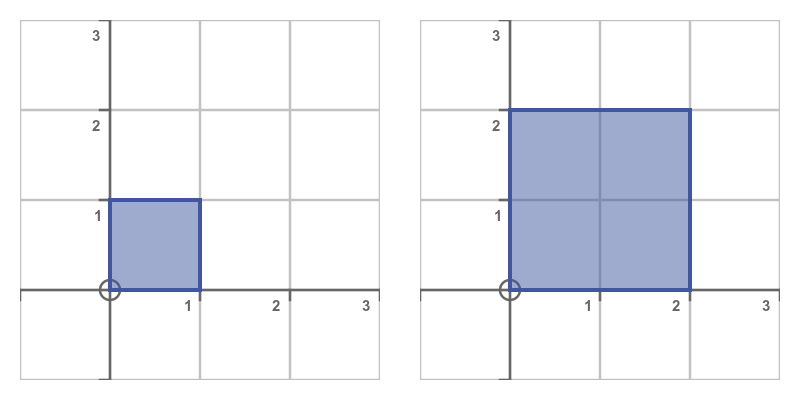
This transform scales everything out from the origin, in other words, it has the centre of enlargement of (0, 0).

A stretch transform scales the shape in one dimension only. Here is the matrix transformation:

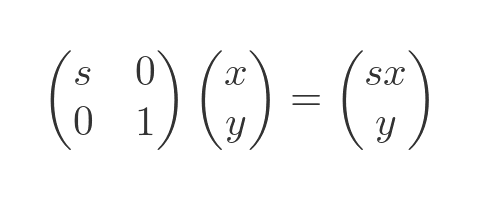
This stretches the square in the x-direction:

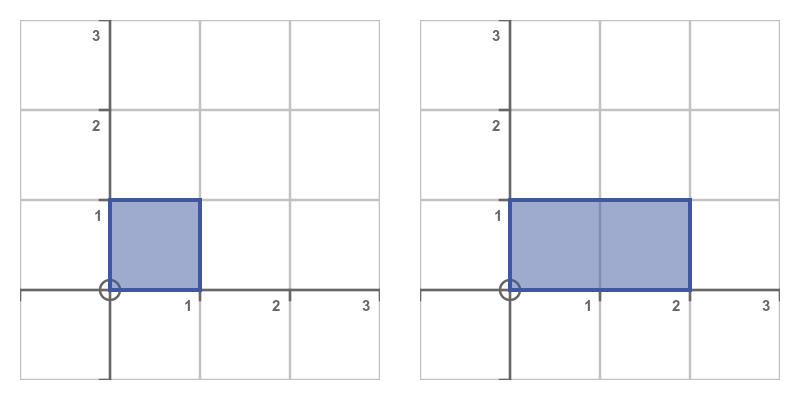
A stretch in the y-direction could be achieved by swapping the 1 and s.

Finally, a squeeze transform scales the shape by s in one dimension only, and by 1/s in the other dimension. Here is the squeeze matrix:

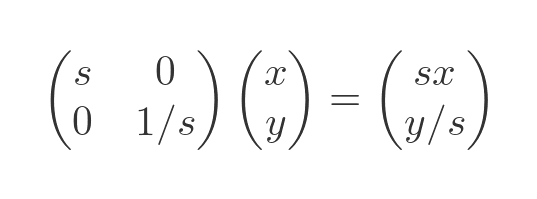
Here is the effect:

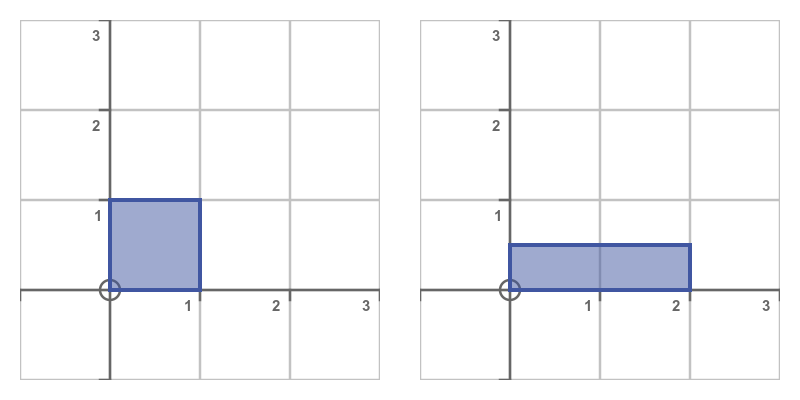
A squeeze transformation preserves area. When a squeeze matrix is applied, the width is multiplied by s and height by 1/s so the area of the shape is unchanged.

Rotation

A rotation transformation uses the following matrix:

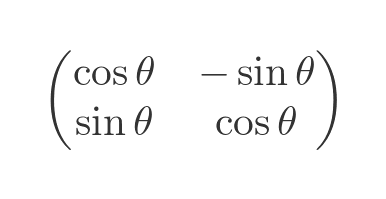
Here is the effect it has on a vector:

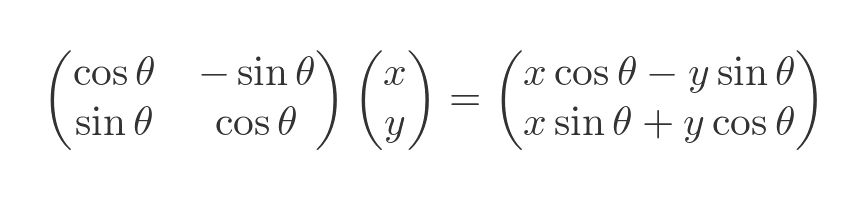
This has the effect of rotating the shape by an angle of θ (30 degrees in this case):

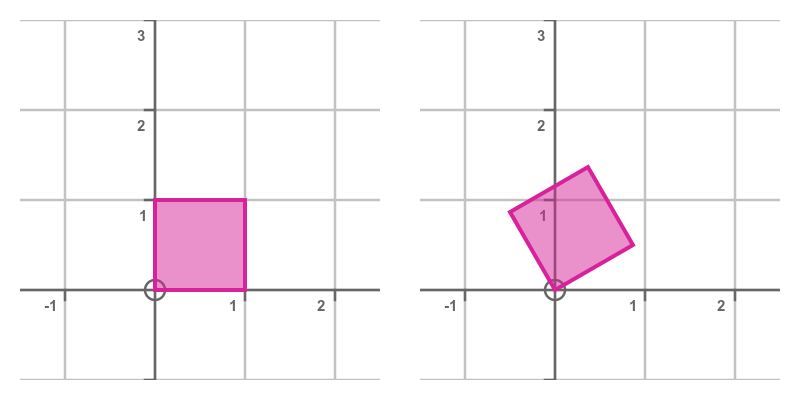
This transform rotates the shape counterclockwise about the origin. That is, it has its centre of rotation of (0, 0). To rotate clockwise, of course, we simply use a negative angle.

Shearing

A shear transformation has the effect of slanting the shape. This matrix shears horizontally:

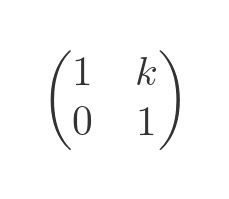
Here is the effect it has on a vector:

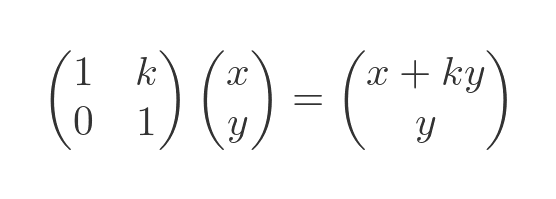
This has the effect of shearing the shape:

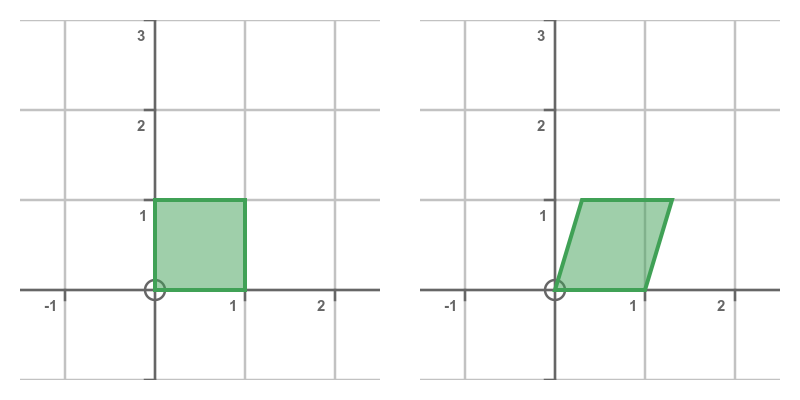
It is also possible to shear a shape vertically, using this matrix:

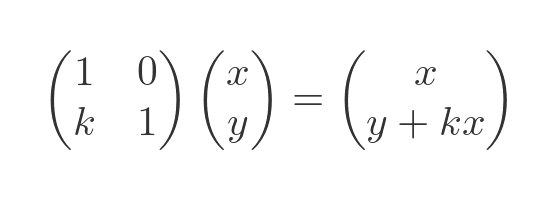
Here is the result:

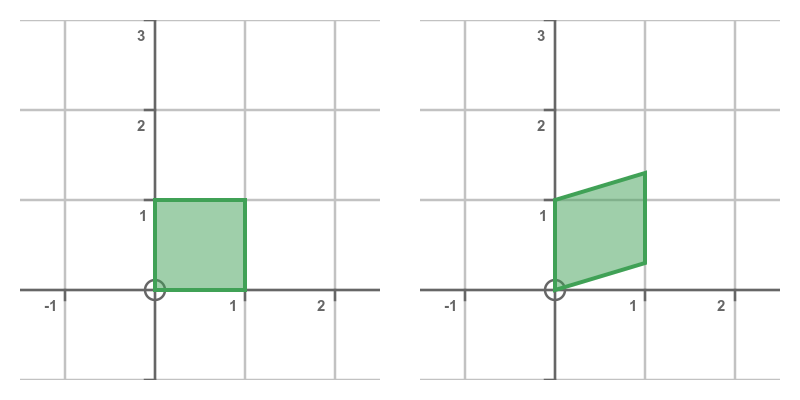
Mirroring

Mirroring a shape across the y-axis can be thought of as being a bit like stretching it in the x-direction, but with a stretch factor of -1:

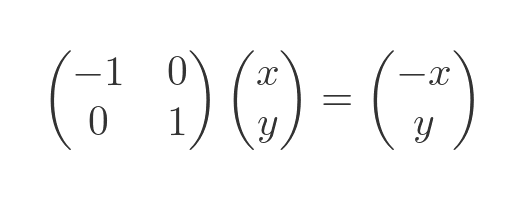
Here is the result:

It is possible to mirror across the y-axis in a similar way.

Translation

Translating a shape means moving it to a different position, without changing its shape or orientation in any way. This diagram illustrates a translation by (1, 2). The square moves by 1 unit in the x-direction and 2 units in the y-direction:

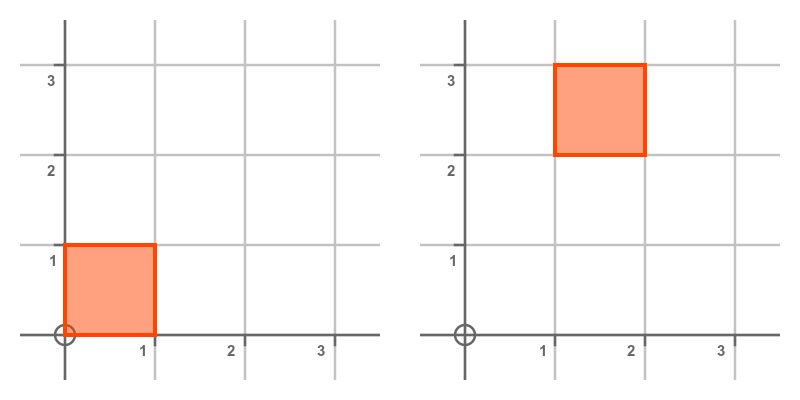
We can represent this by adding 2 vectors, the original position (x, y) and a displacement vector (u, v):

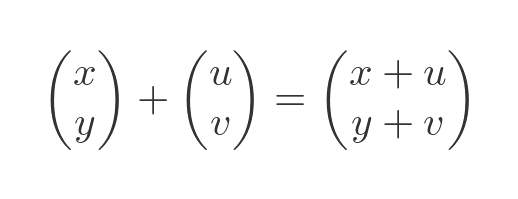
But this isn't ideal. In all the other cases, we used matrix multiplication to represent the transform. It is a bit inconvenient to have to use a different calculation for translation. And in a future article, we will see that we can combine multiple transforms into a single matrix. To do that, we need a consistent way to represent all transformations.

It turns out that we can do this by using a 3 by 3 matrix. We extend our transformation matrix by adding an extra column to the right, containing the transformation values u and v. To keep the matrix square, we add an extra row that always contains 0, 0, 1:

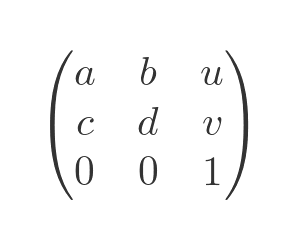
We also need to extend our position vector to be 3 elements long. We do this by adding an extra row element that is always equal to 1.

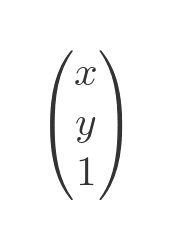
For a translation formula, we set the a, b, c, d values to a unit matrix, and set the u, v elements to contain the translation values. When we apply this matrix to a position vector we do indeed get a translation:

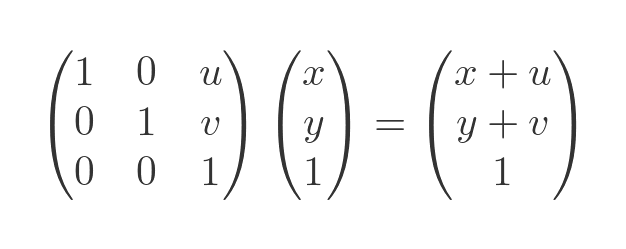
You can verify this by performing a matrix multiplication by hand (or you could use an online matrix calculator) if you wish. The third element of the transformed vector will always be 1 and is discarded after the calculation to leave us with a 2-vector result.

The useful thing about this is that it works for the other transformations too. Let's try it with the squeeze transformation form before. This time we set u and v to 0 because there is no translation:

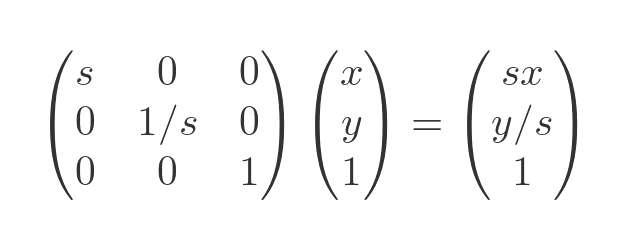
This form works for all transformations and in a later article, we will see how it allows us to combine several transformations into one matrix.

See also

• What is a matrix?
• Determinants
• Matrix inverse
• Combining and inverting transform matrices
• Solving simultaneous equations with matrices
• Introduction to eigenvectors
• Diagonalising matrices