Determinants

The determinant of a matrix is a scalar value (ie a single number) calculated from the elements of the matrix.

In this article, we will look at the definition and some of the uses of determinants. We will also look at some properties of determinants. The determinant is only defined for square matrices.

What are determinants used for?

We can use matrices to perform transformations (scaling, rotation, etc) in 2D or 3D spaces. They are used a lot in computer graphics, for example. The inverse of a matrix represents the inverse transform (for example scaling by 2 and scaling by 0.5 are inverses of each other). Determinants are used in the calculation of inverse matrices. The reason we need the determinant is that it represents the scale factor of a general special transform, as we will see below.

We can use matrices to solve linear simultaneous equations, and again the determinant is used in that calculation.

We also need to know the determinant to calculate the eigenvectors of a matrix. We will cover this in a later article.

Determinant of a 2 by 2 matrix

We will start by looking at how a determinant is calculated. For a 2 by 2 matrix like this:

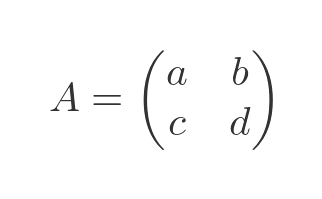
We calculate the determinant like this:

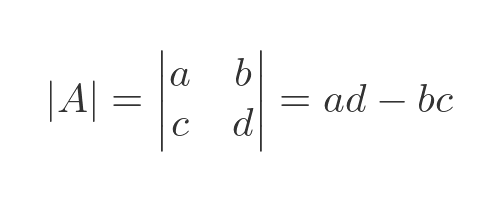
The determinant is a single value formed from all 4 values in the original matrix. For example:

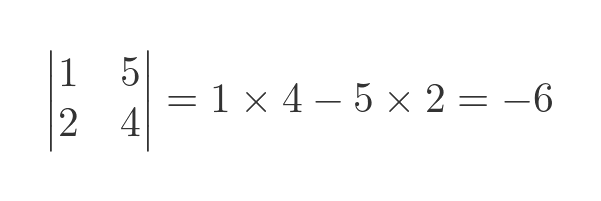
The determinant can also be written like this:

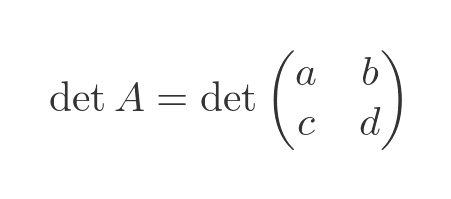
Determinant of a 3 by 3 matrix

Here is a 3 by 3 matrix:

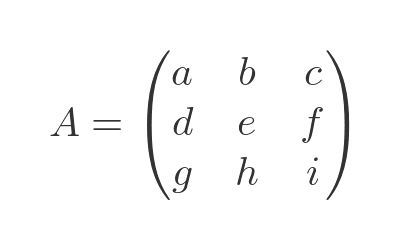
We calculate the determinant like this:

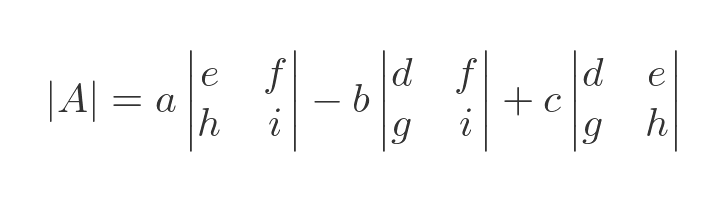
This is called the Laplace expansion. What we have done here is to work along the top row of the matrix to create three terms.

Here is the first term:

Here, we have created a 2 by 2 matrix by removing the row and column that contains element a. The determinant of the resulting matrix is called the minor of the element a. The first term is a multiplied by the minor of a.

Here is the second term:

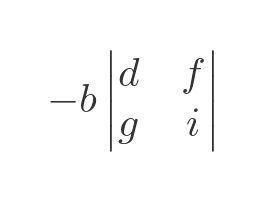
This time we have created a 2 by 2 matrix by removing the row and column that contains element b. The determinant of this matrix is the minor of b. Notice, though that this term is negative.

It is a feature of the determinant that the terms alternate in sign, according to this matrix:

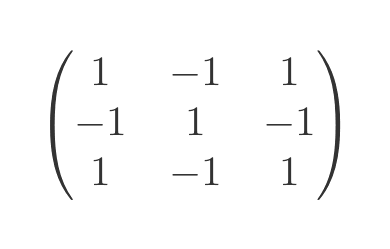
The top left element (1, 1) is always +1, and the other elements alternate in sign, like a chess board. In other words, the sign of element (i, j) is -1 to the power (i + j). This can be extended to a matrix of any size.

The third term, in c is calculated in the same way, and of course, is positive because the position of c in the matrix is positive.

We can express the determinant in terms of minors like this:

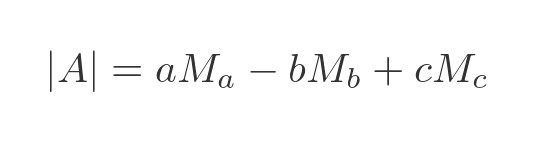
The cofactor of an element is equal to its minor multiplied by its sign (that is, -1 to the power (i + j)). This gives an even simpler expression for the determinant:

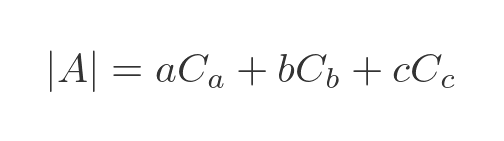
Expanding the 2 by 2 Determinants

Taking the original Laplace expansion:

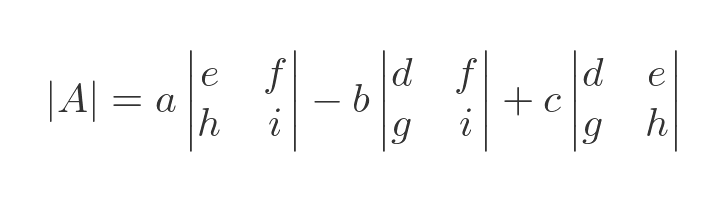
We can expand this out using the definition of the 2 by 2 determinant above:

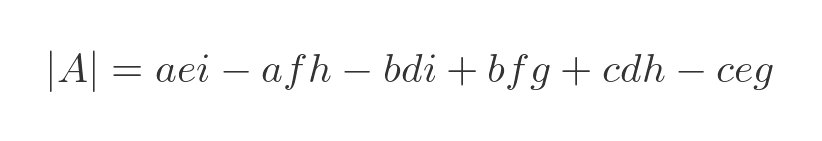
We can use any row or column

We can calculate the determinant using any row or column, and we will get exactly the same result. For example, we could use the second column:

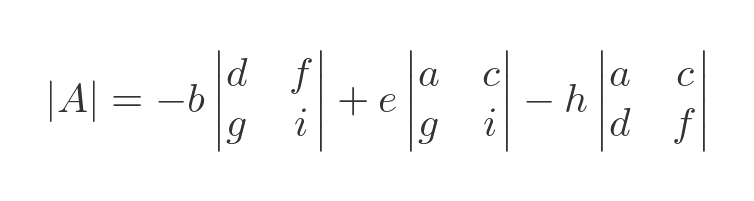
Here the three elements in the second column are b, e, and h. The minor of b is the determinant of the matrix with the row and column of b removed. That is the determinant formed from d, f, g, and i. Similar for elements e and h.

Notice also that the sign of the term in b is negative, because the row and column numbers (1 and 2) add up to an odd number.

If we expand the determinants in the equation above, we will get the same terms as we did when we calculated the determinant using the first row. The terms are in a different order, but the result is the same.

Higher order matrices

If we start with a 4 by 4 matrix:

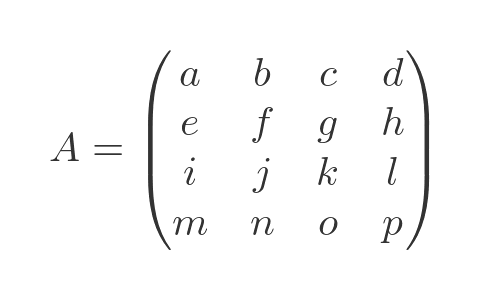
We can expand this using the terms in the first row:

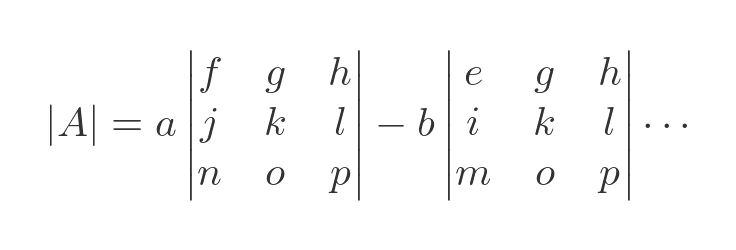
We haven't shown all the terms, but they follow the usual pattern. We can expand the 3 by 3 determinants as we saw before. Using this technique we can, in principle, find the determinant of any n by n matrix, recursively. It is tedious but not complicated.

Another thing to note. The 4 by 4 matrix yields 4 terms, each involving a 3 by 3 determinant. Each 3 by 3 determinant yields 3 terms, each involving a 2 by 2 determinant. Each of those determinants has 2 terms. So the fully expanded factorial has 4! terms. The determinant of an n by n matrix has n! terms

Geometric interpretation

We can use a 2 by 2 matrix to define a transformation in x, y coordinates. If we multiply any vector (x, y) by the matrix we get a new point (x', y'):

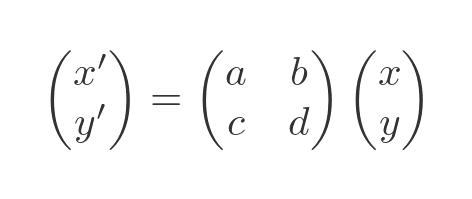
We can transform a polygon (for example a unit square) by applying this transform to each of its vertices. We will use this transform as an example:

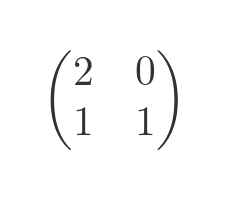
In this table, the left-hand column contains the 4 points of a unit square, and the right-hand column shows these coordinates transformed by the matrix:

This diagram shows the unit square in yellow and the transformed polygon in magenta. The area of the transformed polygon is equal to 2 (whereas the area of the unit square is 1). The determinant of the transform matrix is also 2.

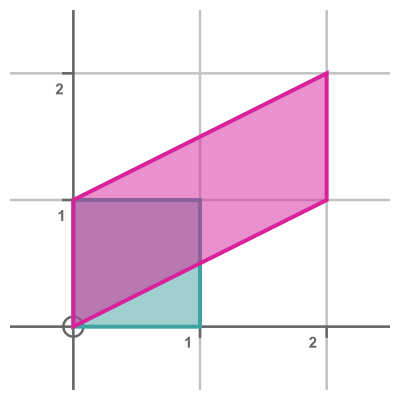
In general, the determinant of a 2D transform matrix is equal to the area scale factor of the transform - that is to say, if the determinant is n then the transformed shape will have n times the area of the original shape.

This also applies to 3D transforms, where the determinant is equal to the volume scale factor.

Properties of determinants

Determinants have several interesting properties. We will mainly look at 3 by 3 matrices, but they also apply to any square matrix. As a basis, we will use this matrix from before:

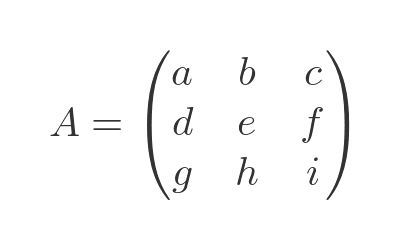
And this equation for the determinant that we saw earlier:

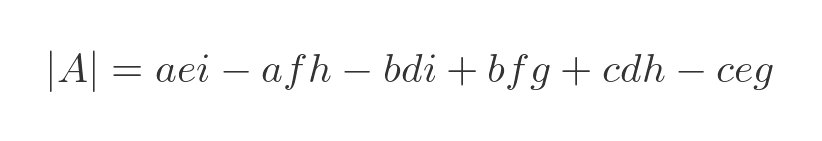
The determinant of a unit matrix is 1. This arises because, in a unit matrix, the diagonal elements (a, e and i) are 1, and all the others are 0. In the equation above, the term aei is 1, and every other term has at least one factor of zero in it. So the determinant is 1.

The determinant of a matrix is equal to the determinant of its transpose. The transpose of A is formed by flipping the matrix over its leading diagonal:

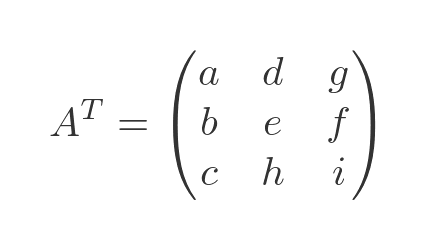
This is the resulting determinant:

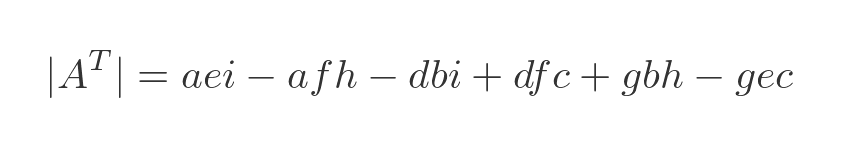
Although all the elements are reordered, we can see by careful inspection that this is identical to the determinant of the original matrix.

Swapping 2 rows of a matrix negates its determinant. (This applies to columns too, as do all the row properties listed below.) Here we have swapped rows 1 and 3:

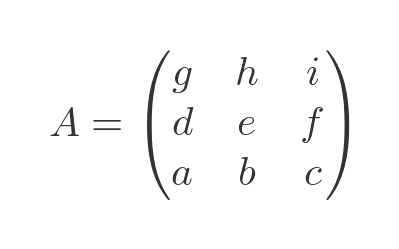
This is the resulting determinant:

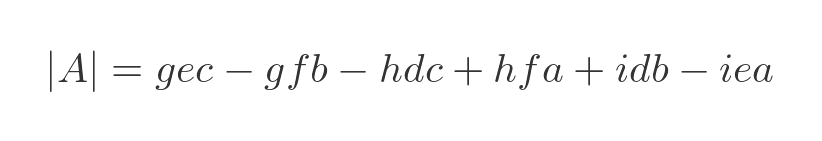
The first term gec corresponds to the term -ceg in the original determinant. Every other term is also the negative of one of the terms in the original, so the whole determinant is negated.

If 2 rows are identical, the determinant is 0. This follows from the previous property - we know that swapping 2 rows negates the determinant. But suppose 2 rows are identical. If we swap those 2 rows it doesn't change the value of the matrix (so the determinant doesn't change), but it negates the determinant. The only way we can negate the determinant without changing its value is if the determinant is 0.

If we multiply all the elements in one row by k, the determinant is multiplied by k. Let's multiply the first row by k:

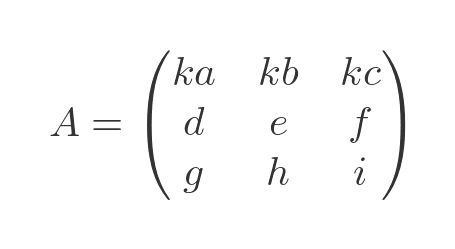
It has this effect on the determinant:

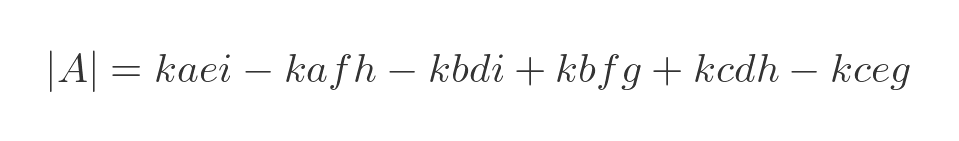
Each term is multiplied by k, so the determinant is multiplied by k.

If we multiply a matrix by a scalar value k, the determinant is multiplied by k cubed. That is assuming a 3 by 3 matrix. For an n by n matrix it is multiplied by k to the power n.

This is similar to the previous example, but this time every element is multiplied by k so the determinant becomes:

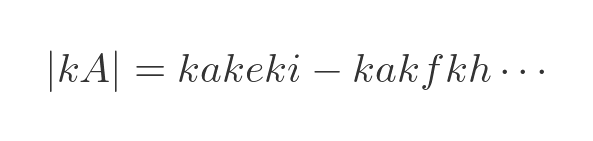
Finally, a matrix is invertible if and only if its determinant is non-zero. What does that mean? Well if you think back to the 2D transform we looked at earlier:

The transform is reversible - it is possible to transform the magenta shape bach into the original cyan shape.

However, we could have used a different matrix to transform the shape, for example:

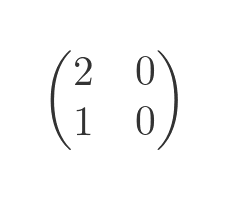
This creates the following transform:

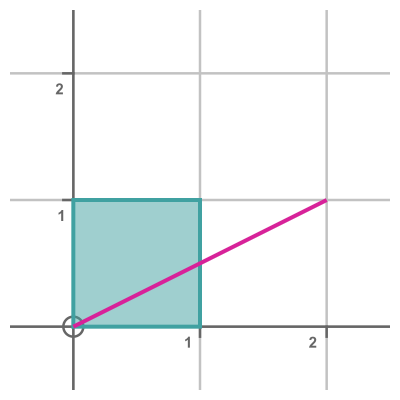
The matrix we used this time has a determinant of 0. This means that all the points from the original unit square are mapped onto a straight line. We can't reverse this transform because some of distinct points in the original shape are mapped onto the same point in the transformed shape.

Notice also that, as predicted, the magenta shape has an area of 0.

See also

• What is a matrix?
• Matrix inverse
• 2D transformation matrices
• Solving simultaneous equations with matrices
• Introduction to eigenvectors