Differentiation from first principles - a to the power x

In this article, we attempt to apply the first principles approach to find the derivative of a to the power x, where a is a constant value that is greater than 0. We will see that it is not quite as straightforward as we might hope.

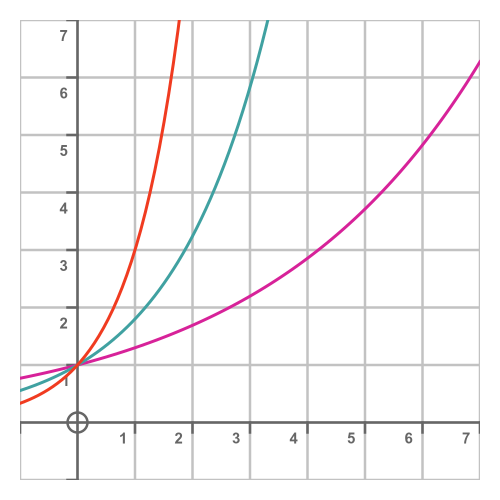
Applying the standard formula

Differentiation from first principles uses the following standard formula to find the derivative of some function f(x):

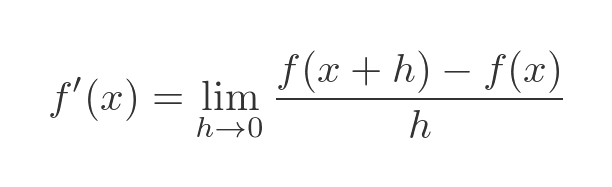
In this case, the function is:

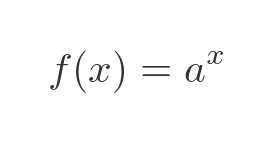
We can use this function in place of f(x) in the previous equation:

Using the product of powers rule we can separate the term in h:

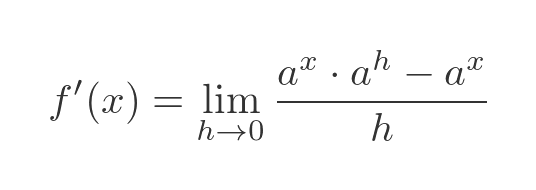
We can then factorise the equation to completely separate the terms in x and h:

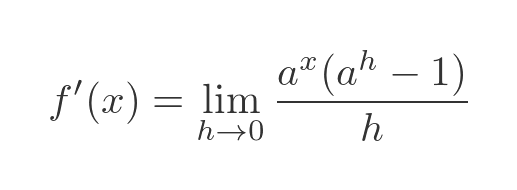
Now the term in x is independent of h, which means it doesn't change as h tends to 0. This means we can bring it outside the limit:

Notice also that the term inside the limit doesn't depend on x at all. This means it is a constant, that depends only on a. So we can write the derivative as:

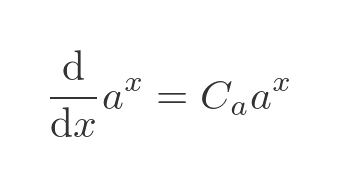
So there we have it. The derivative of a to the power x is equal to some constant C times a to the power x. But what is this mysterious constant C? There are various ways to find it, although since our aim is to find the derivative from first principles we need to be careful about the assumptions behind each method.

Method 1 - it is a standard result

The following is a known, standard result:

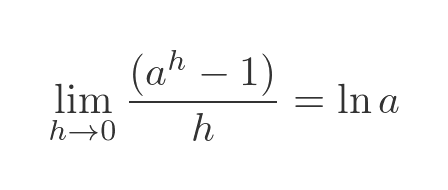
This means that:

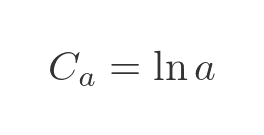
Which gives the result that:

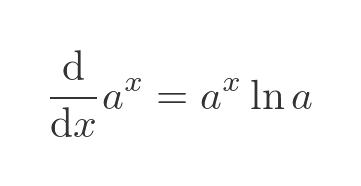
This is the correct answer, but basing it on a standard result goes against the spirit of proof from first principles.

Finding the limit

We would normally find a differential from first principles by evaluating the limit. From the formula above we know that:

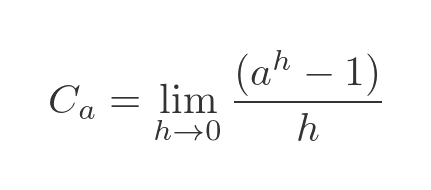
But this is a little problematic:

1. Since a is positive (we stipulated this earlier) then a to the power h tends to 1 as h tends to 0. This means the top line of the limit equation tends to 0 as h tends to 0.
2. The bottom line of the limit equation is simply h which also tends to 0 as h tends to 0.

So unfortunately this limit tends to 0/0, which is indeterminate, so it doesn't help us find C. There are a couple of ways to tackle this.

Method 2 - L'Hopital's rule

L'Hopitals rule can be applied whenever you wish to find the limit of a function that takes the form of a quotient the top and bottom of the quotient both tend to 0:

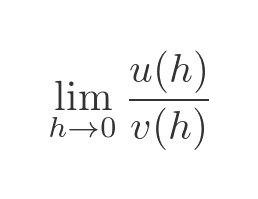
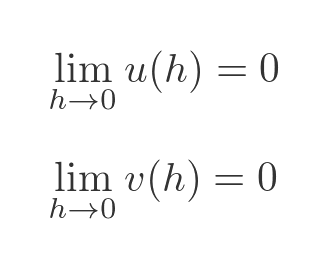
L'Hopitals rule tells us that, in that particular case, the limit can be found from:

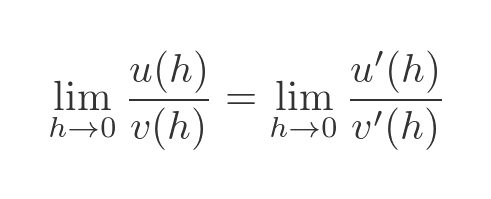
So if we find the derivatives of u and v we should be able to find the limit. This works well in many situations, but in this case, there is a problem. The value of u, the top part of the limit, is:

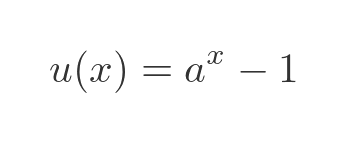
To differentiate that, we need to differentiate a to the power x, which is the exact problem we are trying to solve in the first place. Unfortunately this gets us nowhere.

Maclaurin expansion

The Maclaurin expansion of a to the power x is a standard result:

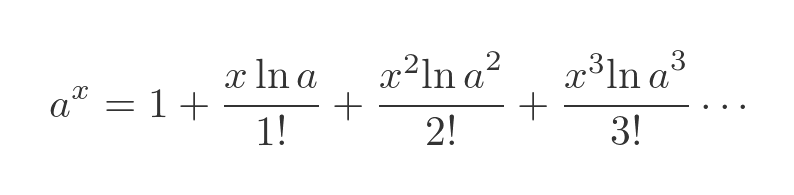
We can use this with the previous formula for Ca:

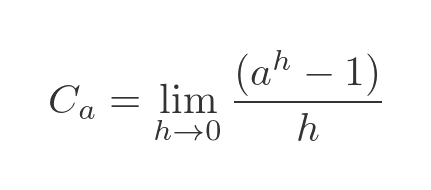
This gives us:

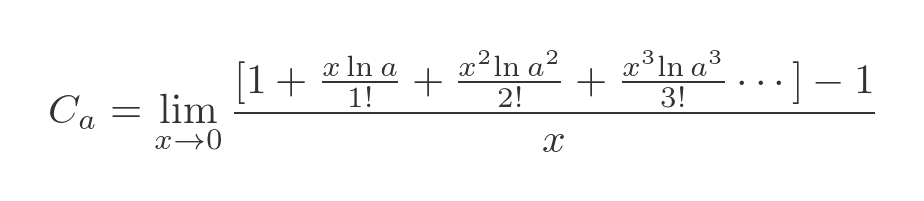
We can cancel out the 1 and -1 terms:

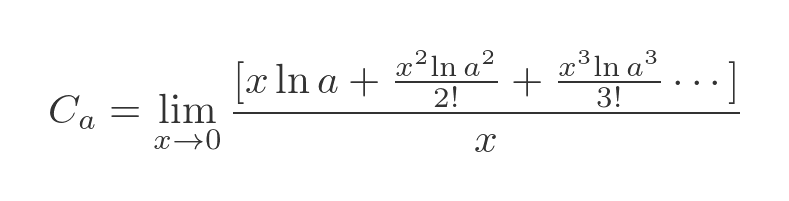
We can cancel out the bottom x term by dividing every term on the top by x:

As x tends to 0, all the terms go to zero except the first ln a term:

This gives us the same result as before. But once again, we are relying on a standard result. And, of course, the Maclaurin expansion is calculated by differentiating the original expression, so it isn't a solution from first principles.

The "best" solution?

Whatever way we look at this problem, we end up going around in a big (but self-consistent) circle. We need to choose a starting point and initial definition that everything else is based on.

There is no best solution, but the one that I find the simplest is based on 3 basic assumptions. First that the exponential function is its own derivative:

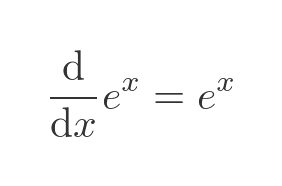
The second assumption is that we can use a (very basic) application of the chain rule to find the derivative of p times x:

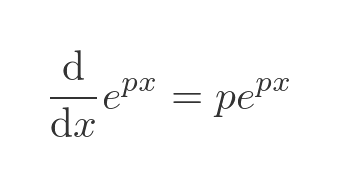
Both of the above rules can be derived from first principles fairly easily.

And finally that the formula for changing the base of the exponential function:

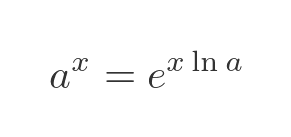
Using these results, we can differentiate a to the x by expressing it as e to the px and applying the chain rule:

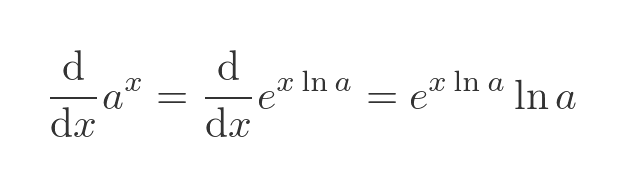
We can then substitute the exponential term with a to the x:

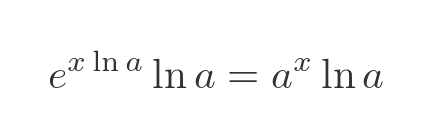
This result isn't directly derived from first principles, but it uses a couple of results that are. It is probably as close as we can get.

See also

• Slope of a curve
• Differentiation from first principles - x²
• Second derivative and sketching curves
• Differentiation - the product rule
• Differentiation - the quotient rule
• Differentiation - the chain rule
• Differentiation - derivative of an inverse function
• Derivative of sine, geometric proof
• Differentiation - L'Hôpital's rule