Derivative of sine, geometric proof

The first derivative of the sine function is the cosine function:

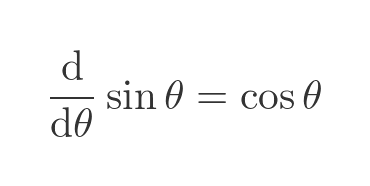
In this article, we will provide a simple geometric proof of this result.

Sine in a unit circle

This diagram shows part of a unit circle, centred at O:

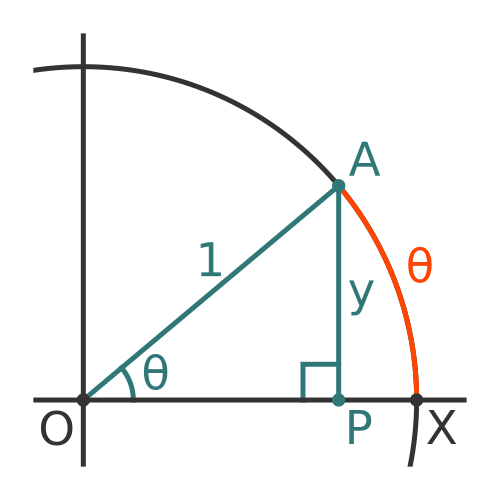
The right-angled triangle OPA has an angle θ at the centre of the circle. We can find the sine of the angle from the standard formula:

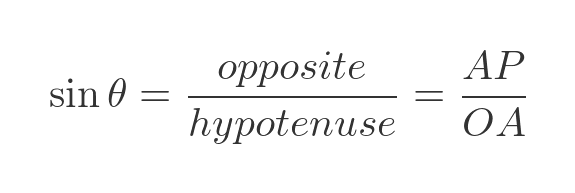
We will represent the length AP as y. Since OA is the radius of a unit circle, it is 1. So the sine of θ is simply:

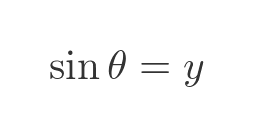
While we are looking at this diagram, it is also worth noting that the arc of the circle between X and A has a length θ. That is because the arc subtends an angle θ at the centre of the circle. The length of an arc is given by rθ (provided θ is measured in radians), and since r is 1 for a unit circle, the length is simply θ. We will use this result later.

Incrementing θ

Here is what happens when we increase θ by a small amount Δθ:

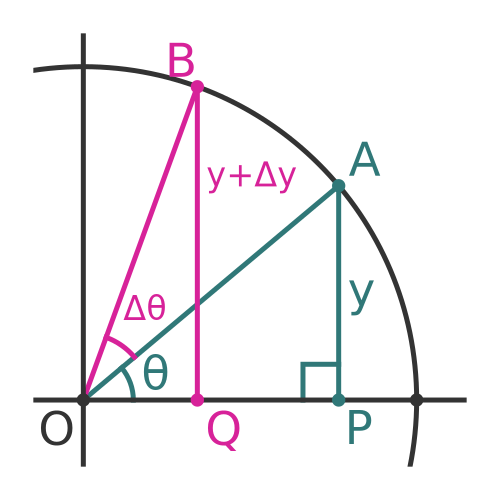
If we draw a radius with an angle of θ + Δθ, it meets the circumference as point B.

We previously noted that AP, the perpendicular height of A from the x-axis, is equal to the sine of θ. We called the distance y:

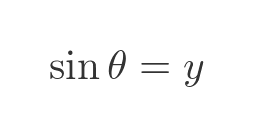
The perpendicular height of B from the x-axis is BQ. Let's call this new distance y + Δy. This is equal to the sine of θ + Δθ:

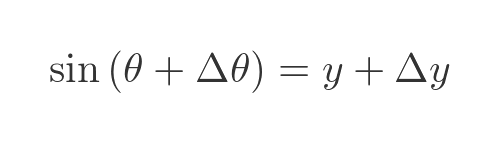
We can now write a difference formula for the change in sine θ, as θ changes:

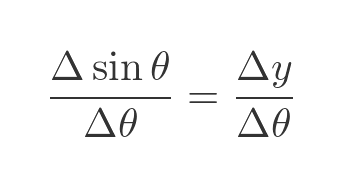
The limit as Δθ tends to zero gives us the derivative of the sine function:

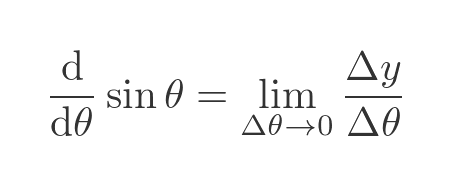
If we can find an expression for Δy as a function of θ, we should be able to solve this equation to find the derivative of the sine function.

Finding Δy

We will now add an extra point C to create a triangle ABC. We will place C vertically above point A and horizontally in line with point B:

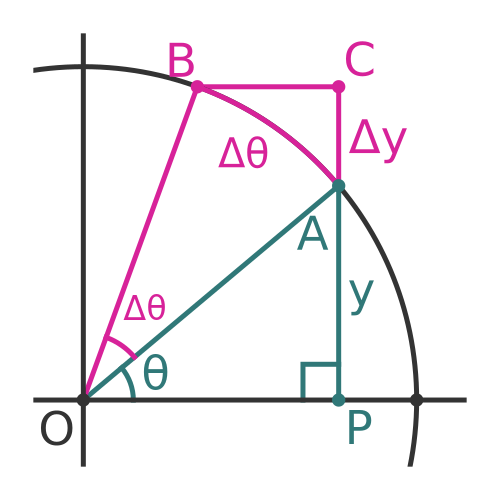
Some observations about the triangle ABC:

• Since AC is vertical and BC is horizontal, angle C must be a right angle.
• Since A is a distance y from the x-axis, and B is a distance y + Δy from the x-axis, side AC has length Δy.
• The arc length AB has length Δθ for reasons we discussed earlier.

Triangle ABC as Δθ tends to zero

As Δθ tends to zero, the arc AB tends towards a straight line, and furthermore, that straight line is a tangent to the circle:

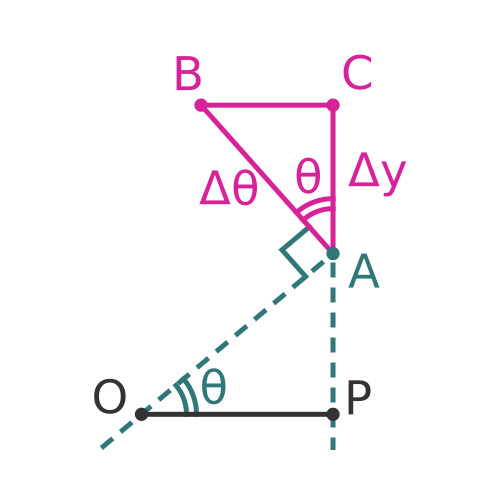
In the limit as AB tends towards a straight line, the length of the line AB tends towards the length of the arc AB, which is Δθ.

Also, since a tangent and a radius of a circle meet at 90 degrees, the angle OAB tends towards a right angle.

It is easy to verify through simple geometry that, when OAB is a right angle, the angle BAC is equal to the angle AOP, which is θ.

Finding the derivative of sine

Here is the triangle ABC, and everything we know about it:

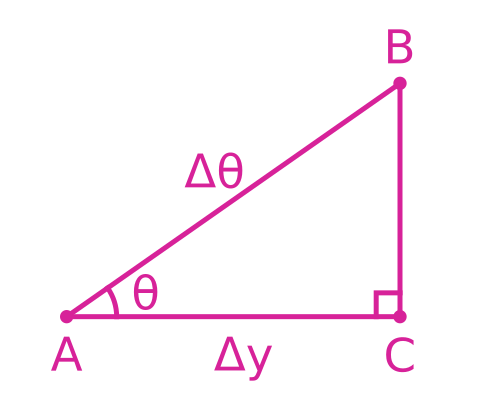
This represents the triangle as Δθ tends to zero. From the triangle, basic trigonometry tells us that:

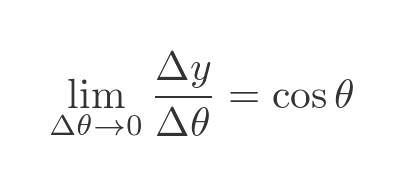
We know from earlier that:

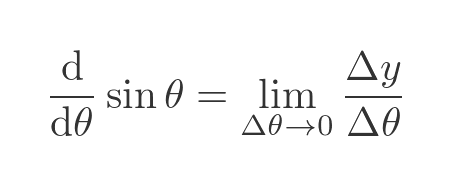
This proves that:

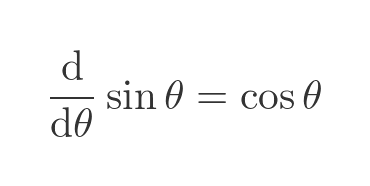
See also

• Slope of a curve
• Differentiation from first principles - x²
• Differentiation from first principles - a to the power x
• Second derivative and sketching curves
• Differentiation - the product rule
• Differentiation - the quotient rule
• Differentiation - the chain rule
• Differentiation - derivative of an inverse function
• Differentiation - L'Hôpital's rule