Differentiation - the product rule

The product rule allows us to find the derivative of the product of 2 or more functions. It provides a simple way to differentiate functions such as:

It is also known as the Leibniz product rule, or sometimes simply the Leibniz rule.

In this article we will give some worked examples of the rule, including applying it to the case of x squared to show that it gives the same result as differentiation from first principles. We will then look at an informal geometric interpretation of the formula, before working through a formal proof. Finally, we will see how to apply it to products of 3 or more formulas.

The rule

If we have a function f that is the product of 2 functions u and v:

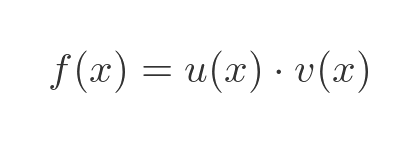
The derivative is given by:

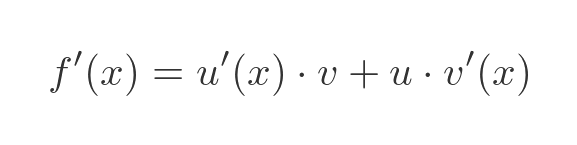
This rule allows us to differentiate any function that is the product of 2 other functions that we already know how to differentiate. The rule can easily be extended to the product of 3 or more functions.

Example

Let's see how this applies to the first example we saw earlier:

This formula is a product of two terms u and v:

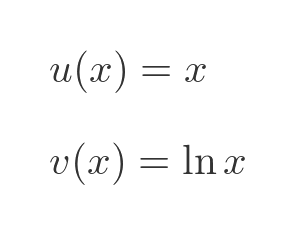
We also need to know the first derivative of each of these functions. These are both standard results:

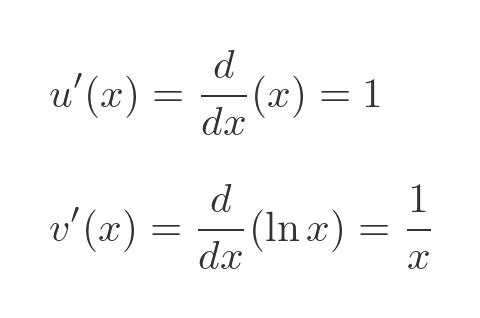
We can now calculate the derivative of f using the product rule we saw earlier:

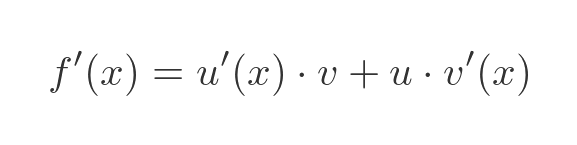
Substituting the terms we calculated earlier gives the final result:

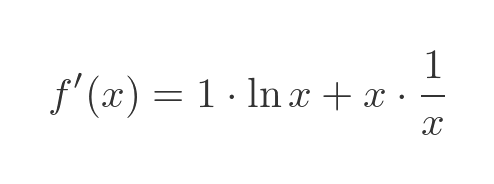
This simplifies to:

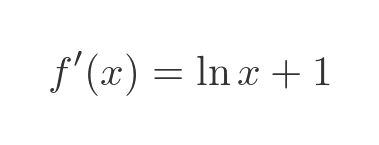
We will look at the another example later in the article.

Verifying the formula for x squared

We can check that this method makes sense, informally, by applying it to a result we already know, x squared. The derivative of this, of course, is 2x.

We can write x squared as a product, x times x:

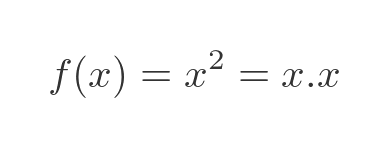
This means that u and v are both equal to x:

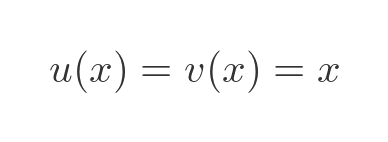
The derivative of x is 1:

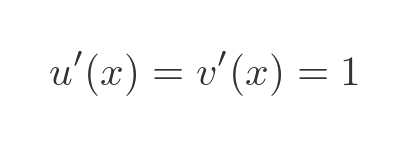
Substituting the values into the product rule formula gives:

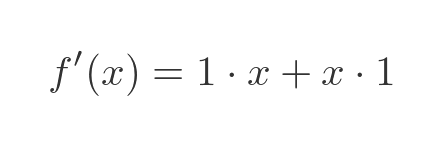
Which simplifies to:

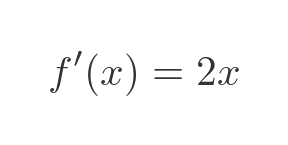
This is exactly what we expected, so we have verified that the product rule works for x squared.

Geometric interpretation of the general case

If f(x) is the product of 2 functions u(x) and v(x), we can represent the value of f(x) as the area of a rectangle with sides u(x) and v(x). This is shown on the left here:

Now let's suppose we increment x by a small amount Δx. This caused u to change by a small amount Δu and v to change by a small amount Δv. That is shown on the right, above.

Incrementing x adds two orange rectangles to the area. The right-hand rectangle has area Δu by v, and the top rectangle has u by Δv.

There is also a tiny yellow rectangle size Δu by Δv. As Δx gets very small, this rectangle gets smaller much more quickly than the two orange rectangles, so we will ignore it in our calculations (we will justify this in the formal derivation later).

So the approximate change in f as we change x by Δx is given by:

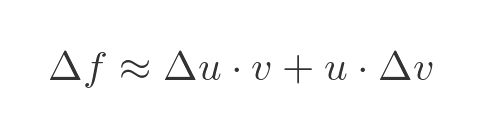
Dividing through by Δx we find the approximate rate of change:

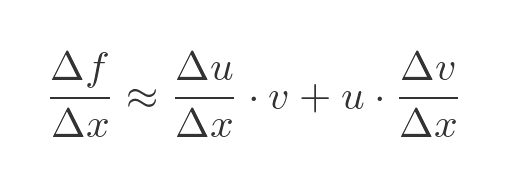
As Δx tends to 0 this resembles the product rule formula:

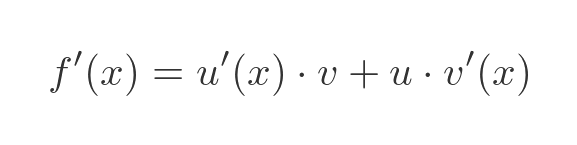
Proof

The proof of the product rule isn't particularly difficult, it is quite similar to the geometric interpretation we have just looked at. But it has quite a few stages, so we will go through it one step at a time. We will be proving the result using the limit definition of the derivative:

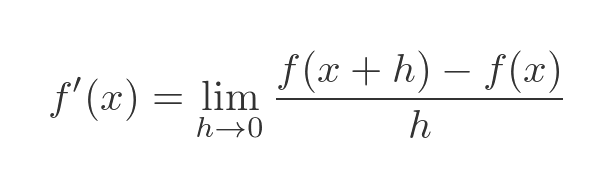
First we replace f with u times v:

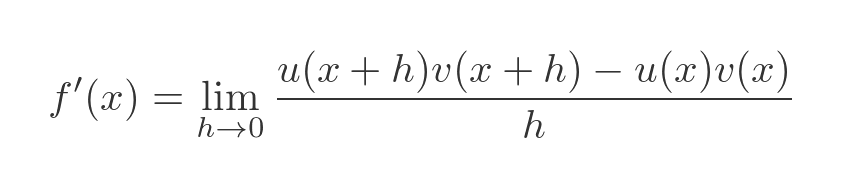
The next step isn't particularly obvious, but the reason for it will be clear in a little while. We are going to add this expression into the limit clause:

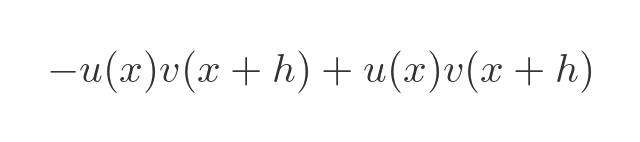
Since this expression has two identical terms, one positive and one negative, it is equal to 0. That means that if we add it to one side the equation will still be valid. Here is the equation with the extra expression added:

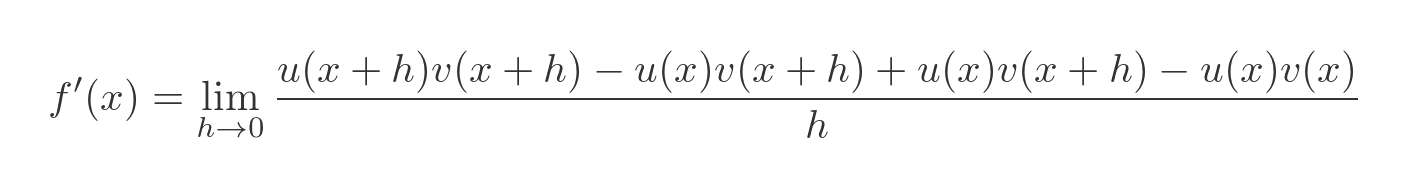
Now we will split the limit into two parts:

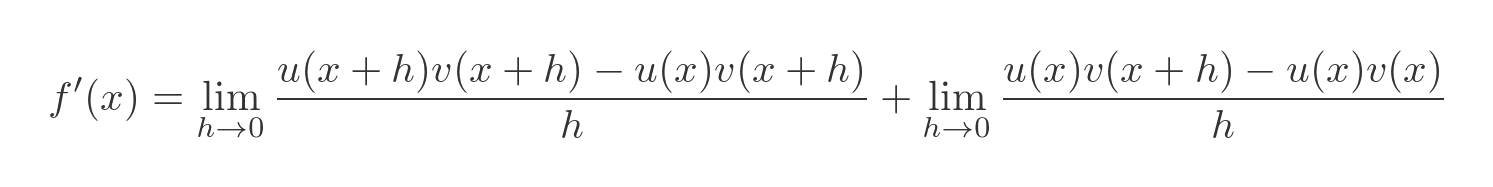
We will call these two parts a and b, and deal with them separately:

You can perhaps start to see why we added the strange expression earlier. It means that a has a factor of v(x + h) and b has a factor of u(x). Here is what happens if we take the common factor out of the expression for a:

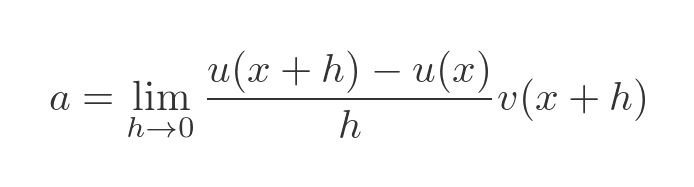
Now as h tends towards 0, the term v(x + h) tends towards v(x). And since v(x) is independent of h, we can take it outside the limit:

Notice now that the limit term is equal to the definition of the first derivative of u. so we can write a as:

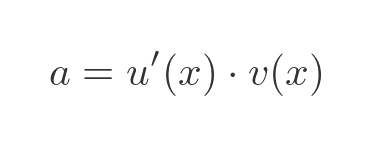
You might now be able to see where this proof is going. The expression for b has a common term in u(x) that we can extract, giving:

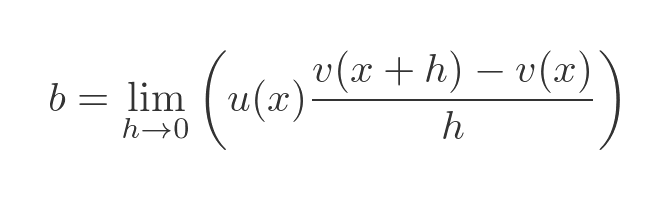
Again, u(x) doesn't depend on h so we can take it outside the limit:

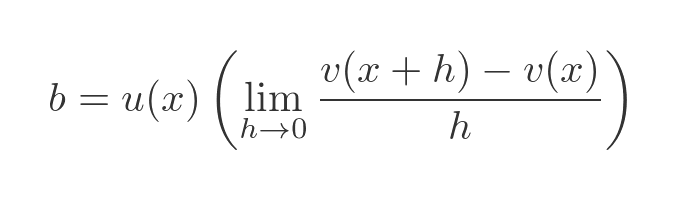
Now the limit term is equal to the definition of the derivative of v, so we can write:

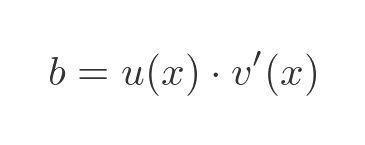
Finally, since f' = a + b we have:

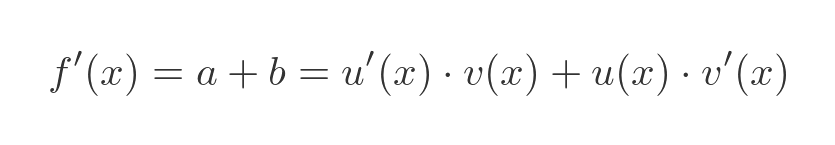
This proves the product rule.

Another example

Now we will apply this to another example:

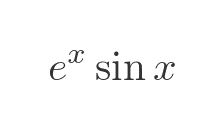
This time f is the product of these two functions, u and v:

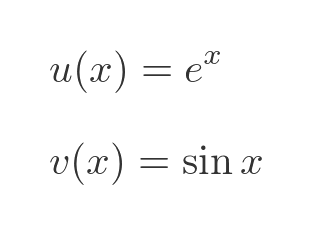
The derivatives of u and v are standard results:

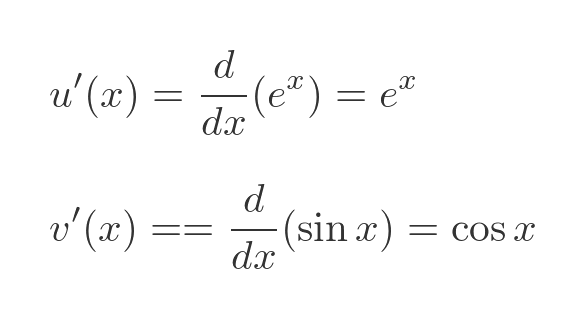
If we plug these results into the product rule formula we get:

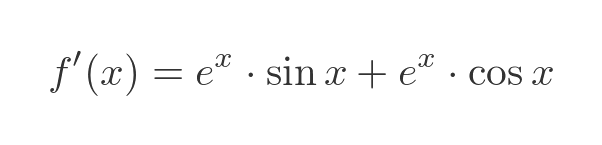
This can be simplified to:

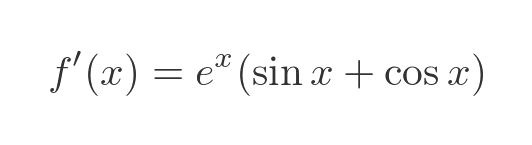
The sin and cos terms can also be simplified (this is a standard result that we won't prove here):

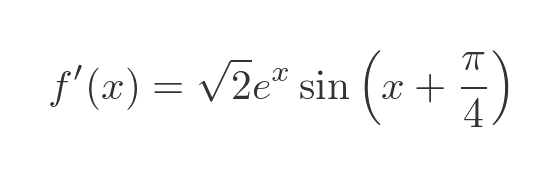
Applying the product rule to 3 (or more) functions

The product rule can be applied to the product of 3 functions:

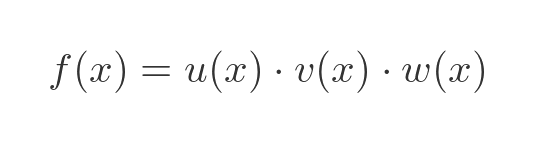
In that case, the rule is:

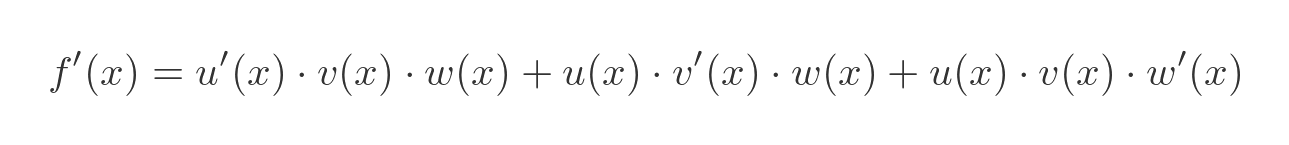
To gain an intuitive understanding of this rule, we can consider a cuboid of sides u(x), v(x) and w(x), like this:

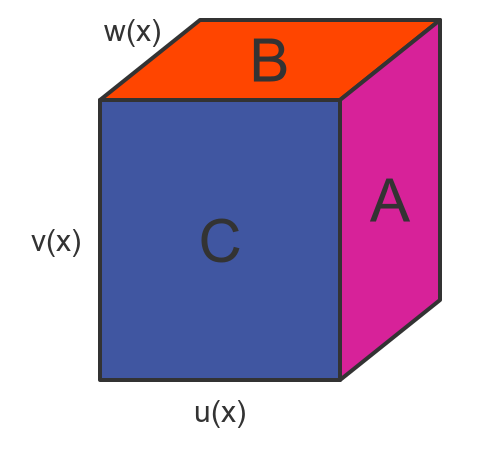
The volume of the cube represents f(x), the product of the 3 functions. This is analogous to the rectangle we used in the 2-function case.

When we increased x by Δx, the 3 faces A, B and C move, changing the volume of the cuboid. Face A moves by an amount Δu, and since the area of the face is v(x) by w(x), the change in volume is Δu.v(x).w(x). Side B moves by an amount Δv and changes the volume by an amount u(x).Δv.w(x). Side C changes the volume by an amount u(x).v(x).Δw.

As Δx tends to zero this gives the differential equation above for the 3-function product rule. This can also be formally proved in a similar way to the 2 function proof we saw earlier. The rule can be extended to products with 4 or more functions, following the same pattern.

See also

• Slope of a curve
• Differentiation from first principles - x²
• Differentiation from first principles - a to the power x
• Second derivative and sketching curves
• Differentiation - the quotient rule
• Differentiation - the chain rule
• Differentiation - derivative of an inverse function
• Derivative of sine, geometric proof
• Differentiation - L'Hôpital's rule