Why does complex number multiplication cause rotation?

Complex multiplication has the effect of rotating the position of a number in the complex plane. In this article, we will see an intuitive explanation for this effect.

An alternative explanation for this effect comes from Euler's formula.

Multiplying two complex numbers

The left hand image below shows two complex numbers, a = 2 + 2i and b = 1 + 3i, on an Argand diagram:

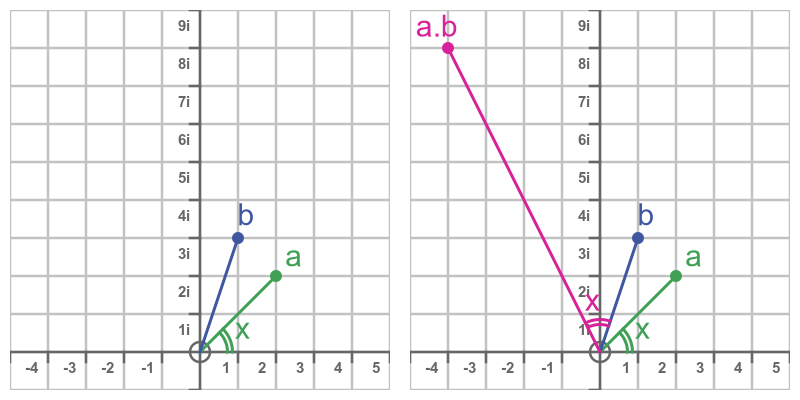
The angle x is the angle that the point a makes with the x-axis.

The right-hand diagram shows a.b, the complex product of a and b:

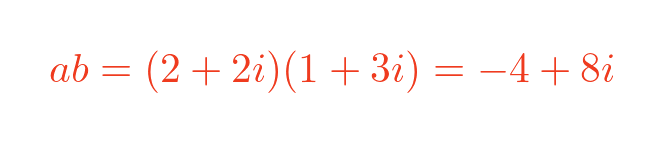
The angle between a.b and b is also the angle x. In other words, multiplying b by a rotates the point b about the origin by the angle that a makes with the x-axis.

The length of a.b is also equal to the length of a multiplied by the length of b.

We can repeat this with a different complex number, c = -2 - i, again using the same value a:

The right-hand diagram shows the product a.c. This time c is rotated by the same angle x to give the product a.c.

Adding complex numbers vs adding vectors

We would like to understand what it is about complex numbers that make multiplication behave this way. We will start with a slight aside, looking at complex number addition vs vector addition.

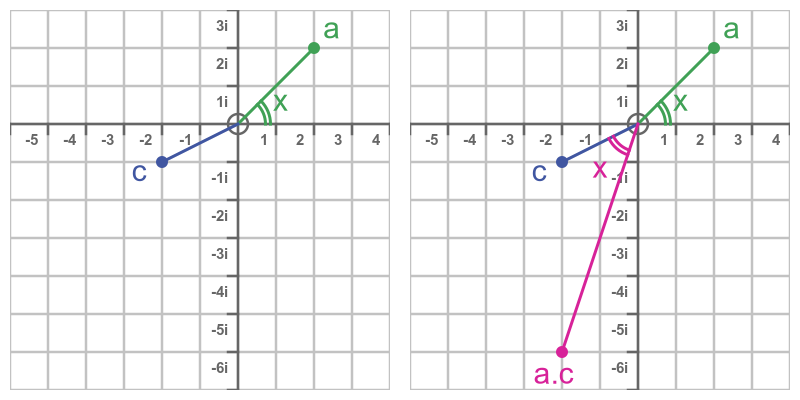
This vector diagram shows what happens when we add the two vectors:

• a, the vector (3, 2)
• b, the vector (1, 4)

We simply add b to the end of a, so the sum is (4, 6).

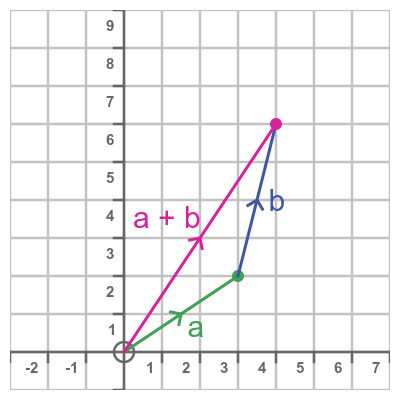
This image shows what happens when we add the two complex numbers on an Argand diagram:

• a = 3+ 2i
• b = 1 + 4i:

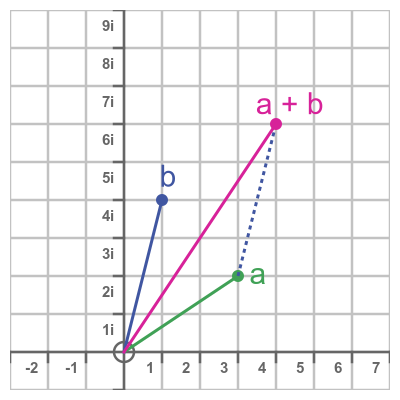
This works in a similar way. We add the real parts and the imaginary parts separately, in much the same way that we added the x and y components of the two vectors together in the previous example. And the result is the same, 4 + 6i, which is equivalent to the vector (4, 6).

Multiplying complex numbers vs multiplying vectors

We will now look at complex multiplication in more detail. We will use two general complex numbers:

• d = s + t i
• e = u + v i

If we multiply out d and e we get this:

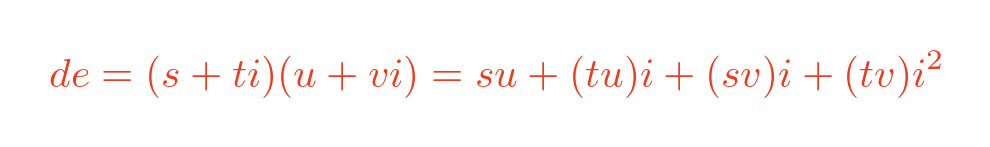
Since i squared is -1, we can simplify this:

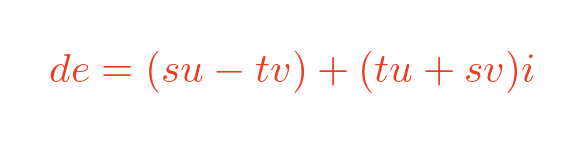
We can't directly compare multiplying complex numbers with multiplying vectors, because there is no way of multiplying two 2-vectors to give another 2-vector as a result. Vectors only support dot products (which produce a scalar value) or cross products (which only apply to 3-vectors, not 2-vectors).

However, if we premultiply a 2-vector (e in this case) by a 2 by 2 matrix, we get a 2-vector:

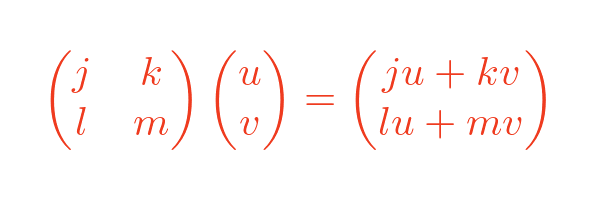
Notice that the resulting vector has a similar form to the result of the complex number multiplications. Each part of the vector consists of a term in u and a term in v. If we choose particular values for j, k, l and m we will get a vector that looks exactly like the previous complex number. Like this:

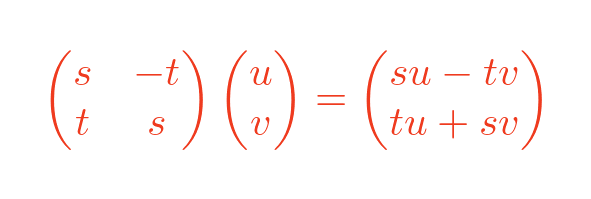
This tells us that there is a relationship between complex number multiplication and vector multiplication. These two calculations give the same result (in complex or vector form)

• Multiplying two complex numbers d and e.
• Premultiplying the vector e by a special matrix containing the values in d.

Let's try this with a = 2 + 2i and b = 1 + 3i from the first example at the start of the article. We will form a matrix from the values in a, and a vector from b, and multiply them together:

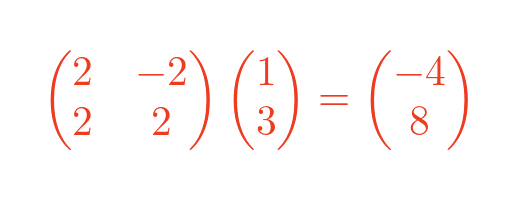
This, of course, gives the same result as the complex multiplication, which was -4 + 8i.

Expressing the matrix in polar form

To understand the effect of the matrix, it is useful to express the vector d in polar form:

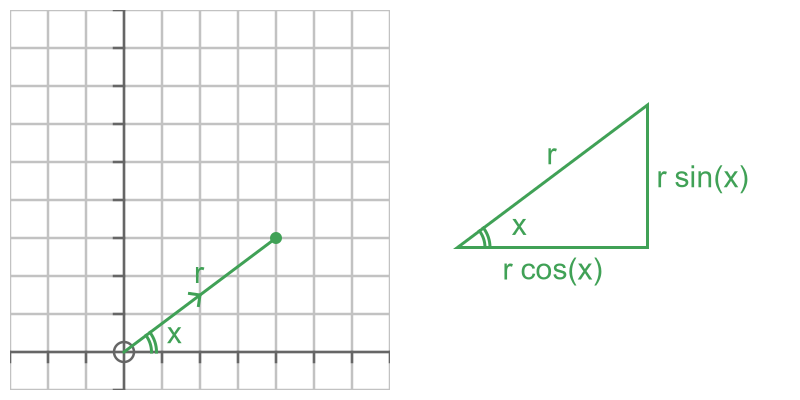
The vector d has length r and makes an angle x with the x-axis. So it can be expressed in polar form as:

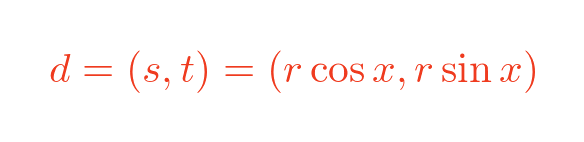
We can apply these values for s and t to the previous matrix:

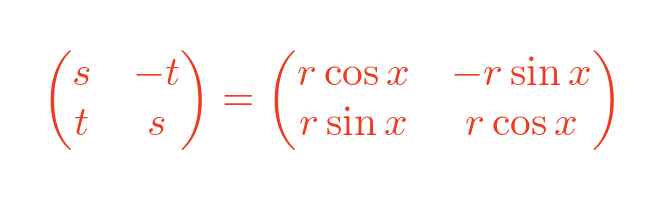
So we now know that multiplying two complex numbers d and e is equivalent to premultiplying the vector e by a special matrix made from the length and angle of d.

Identifying the matrix

So what is this special matrix? Well to help us find out, we can extract the common factor r into a separate matrix, like this:

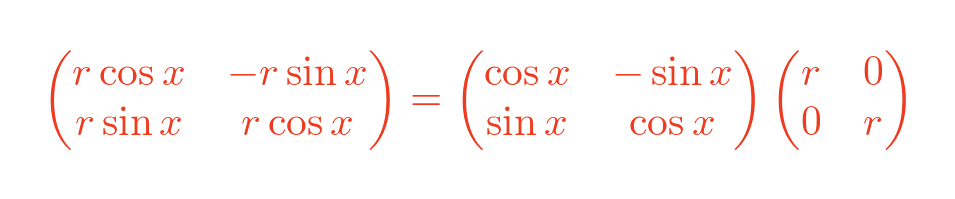
You can easily verify this by multiplying the two matrices together.

But how did we know to do this in the first place? It is because the right-hand matrix (using r) is a well-known transformation. It scales the 2d plane by a factor r.

The left-hand matrix (using x) is also a well-known transformation. It rotates the 2d plane by angle x. counterclockwise, about the origin.

So this tells us that multiplying two complex numbers d and e is equivalent to scaling the vector e by r and then rotating it by x, where r and x are the polar coordinates of d.

This explains why complex multiplication causes rotation.

Complex numbers have many properties and have uses in many branches of maths and science. One of those properties is the ability to easily and intuitively represent scaling and rotation.

See also

• Imaginary and complex numbers
• Complex number arithmetic
• Argand diagrams
• Modulus-argument form of complex numbers
• De Moivre's theorem
• i to the power i
• Euler's formula - proof
• Complex powers and roots of complex numbers
• Semiprocal numbers - z to the power i
• Complex polynomials
• Complex number trigonometry functions