Complex number trigonometry functions

In this article, we will see how to calculate the sine, cosine and tangent of a complex variable z. In the process, we will discover how the trigonometry functions sin and cos are related to the hyperbolic functions sinh and cosh.

To do that, we need to understand what it means to find the sine of a complex number. We know that the sine of a real value θ can be defined as the opposite side over the hypotenuse of a right-angled triangle with angle θ. But it isn't obvious how that applies when the angle is a complex number.

So we will first look at some other ways of interpreting complex trig functions. Then, with the help of Euler's formula and the hyperbolic functions, we will derive useful formulas for doing complex trigonometry using familiar functions of the real domain.

Alternative interpretations of the sine function

The sine function isn't just about triangles, of course. We also know that sine, viewed purely as a mathematical function, has a special property. The second derivative of the sine function is the negative of the sine function:

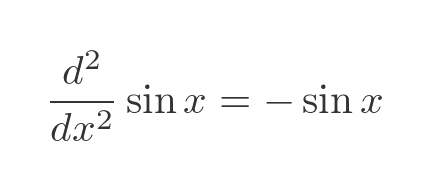
This means that, give or take a couple of constants, the sine function is the solution to the second-order differential equation:

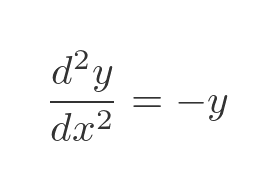
This is the formula that governs, among other things, the motion of an ideal pendulum.

We also know that the sine function can be expressed as a Maclaurin series:

There are similar results for the other trig functions. It is possible to differentiate complex functions, and it is possible to calculate polynomials for a complex variable, so we have good reason to expect that these mathematical functions can be applied to complex numbers.

Unfortunately, these interpretations don't directly help in finding an expression for the complex versions of the functions. We will need to take a slightly different approach to that.

What are we hoping to achieve?

It is worth taking a step back and asking what we are hoping to get out of this. If we have some real function f(x), and we are convinced that it works with complex numbers too, then of course we can just call it f(z). Job done.

The problem is that we know nothing about f(z). We might not even know how to calculate f(z) for any particular value of z. In the case of the sine function, we can calculate its approximate value, using the Maclaurin expansion. We can even calculate its derivative, but that will be in terms of the complex cosine function, which is equally mysterious.

What we don't know is anything about the nature of the function. Compared to all the well-known properties of the real sine function, the complex sine function is a closed book.

What would help with that? Well, perhaps if we could split the function's result into real and imaginary parts, that would help. That is, if we could express f(z) like this:

Here, the real part of the result is u(x, y), a real function of two real variables - the real and imaginary parts of z. The imaginary part of the result is v(x, y), also a real function of the same two real variables. If u and v relate to functions that we already know about, even better.

Of course, complex functions are never going to be as easy to get to grips with as real functions. That is because the input is 2-dimensional, and the output domain is also 2-dimensional.

An example - imaginary exponential function

One example you might be familiar with is the imaginary exponential function:

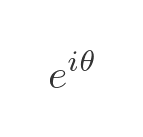
We know from Euler's formula that this can be written as:

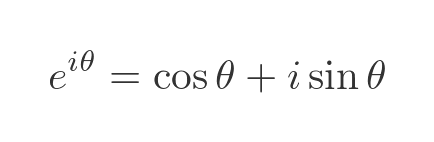
Although this involves an imaginary argument rather than a general complex argument, it follows the pattern we described earlier. We can calculate the real and imaginary parts of the result as separate real functions.

As an aside, it is fairly easy to extend this to a complex argument:

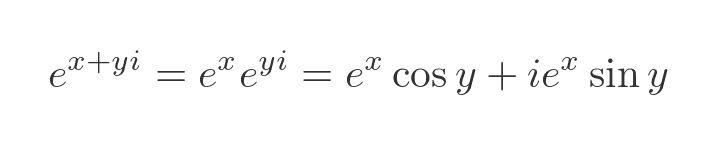
For our purposes, the imaginary version of the formula is all we need.

Sine and cosine as imaginary functions

Euler's formula provides a useful link between sine, cosine, and the realm of imaginary numbers. Here is Euler's function again, with its equivalent for negative θ:

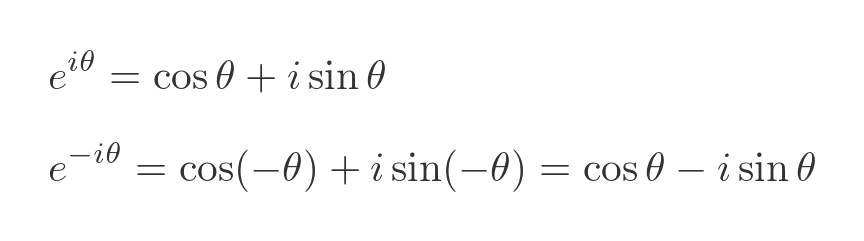
If we add these two equations, it allows us to express the cosine function in terms of imaginary exponents:

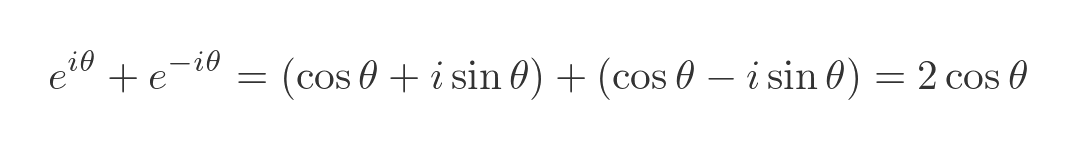
This simplifies to:

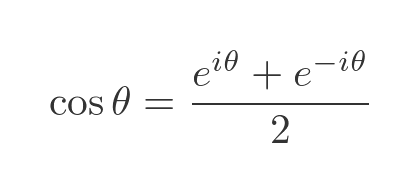
We can do the same thing for sine, by subtracting the two equations:

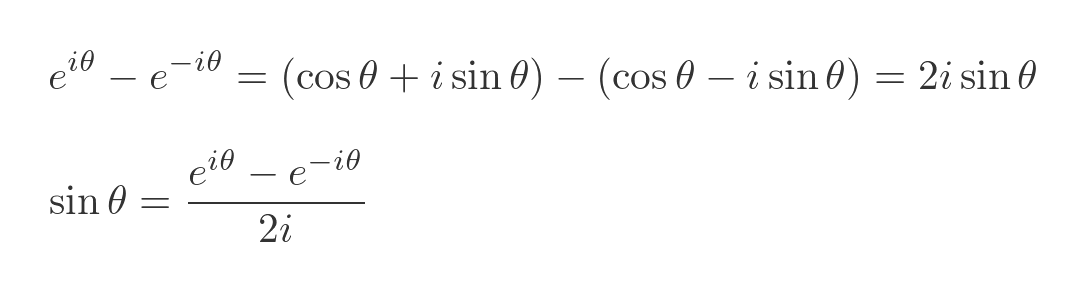
This gives us a couple of slightly strange equations for sine and cosine in terms of imaginary exponential functions. It isn't exactly what we need, but it is a step closer.

Hyperbolic functions

If you are familiar with the hyperbolic functions, the formulas above might look familiar. The hyperbolic sine function, sinh is defined as:

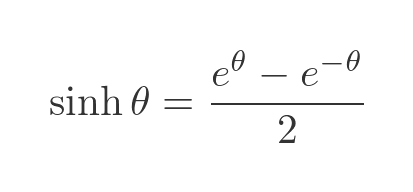
The hyperbolic cosine function, cosh is defined as:

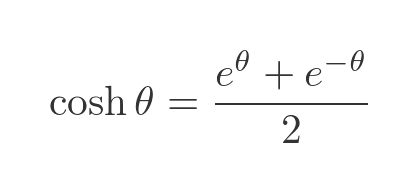
These will become quite useful in a little while.

Sine and cosine of imaginary values

This is where it starts to get interesting. What if we take the previous expressions for sine and cosine, but apply them to an imaginary argument?

The first question is, can we do that? Is it valid? We won't prove it here, but we can justify it. We know that the exponential function can be applied to an imaginary value. If we define the function using its Maclaurin expansion, then it is simply a polynomial:

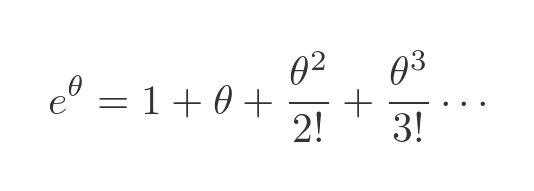
There is no reason we can't use a complex value in a polynomial. Similarly, we can define sine and cosine by their Maclaurin expansions, so again there is no reason we can't use an imaginary argument:

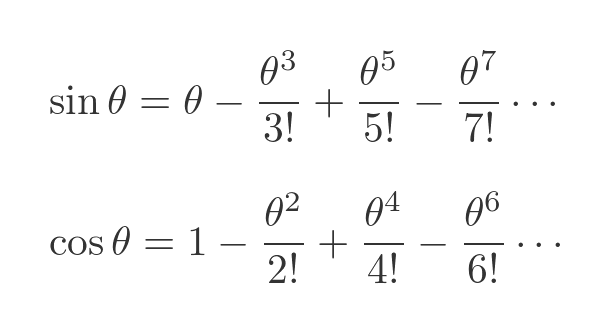
Given that, what is the sine of an imaginary number? We can find from the previous definition of sine, with an argument of iθ:

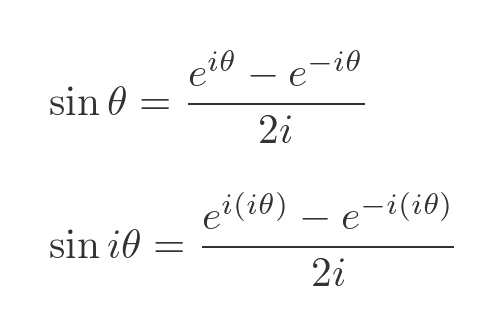
h exponents contain a factor of i times i, which we can simplify to -1:

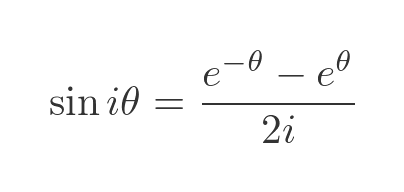
Remember, also, the 1/i is equal to -i, so we can move the i term out of the denominator. We then swap the terms in e and remove the negative:

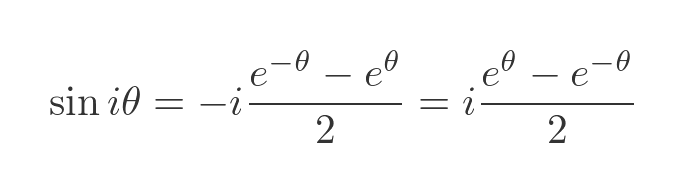
The fraction term now is the definition of the sinh function. So we have this nice result:

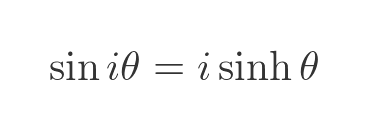
We can do something very similar with the cosine of an imaginary value:

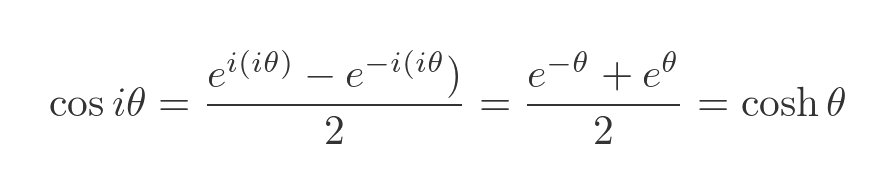
We now have everything we need to find the sine and cosine of a complex number.

Complex sine

To deal with the complex number case, we will make use of the standard formula for the sine of the sum of two angles:

For a complex number x + iy we will substitute the real part x for A, and the imaginary part iy for B:

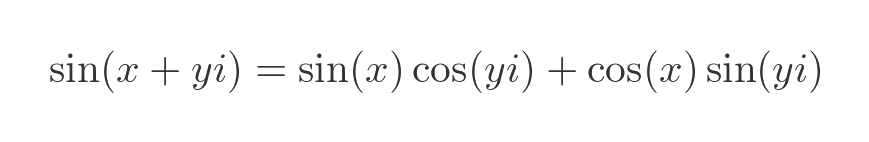
Can we do that? We won't prove it here, but it can be proven using the exponential forms of sine and cosine from earlier.

Now we have a couple of terms in sin(iy) and cos(iy). We know how to handle those by converting them to hyperbolic functions. Substituting those gives us:

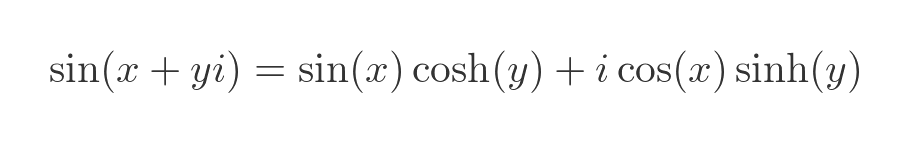
Here is a colour map of the real and imaginary parts of the complex sine function:

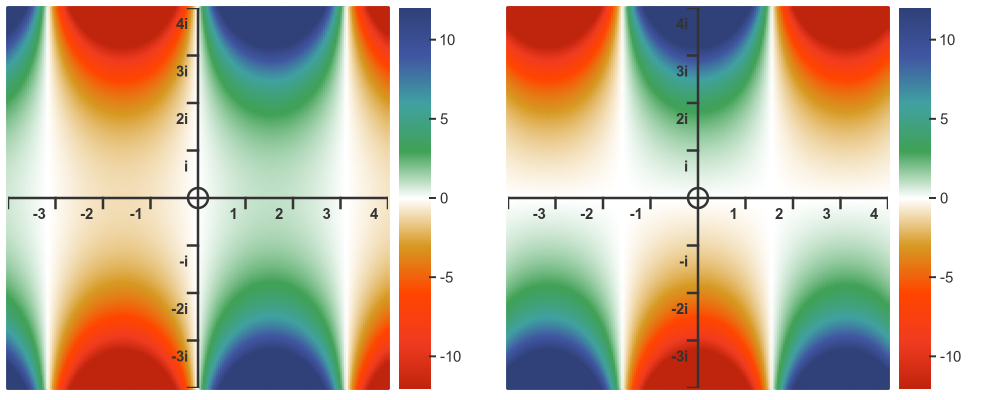
Here is a 3d graph of the same thing:

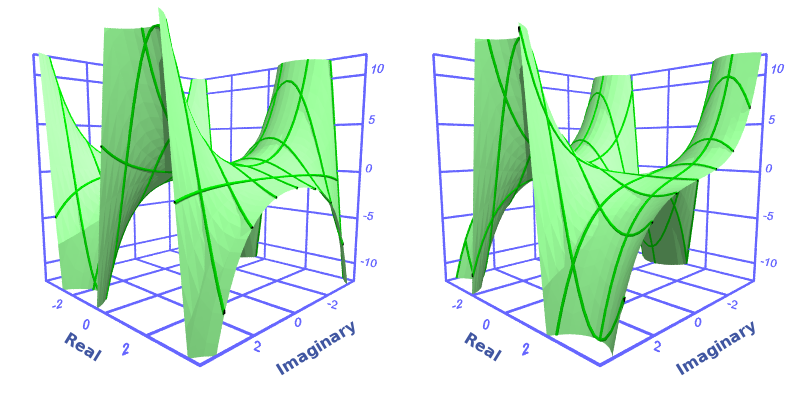
Complex cosine

The complex cosine function can be calculated in a similar way to the sine using the formula for the cosine of a sum of angles:

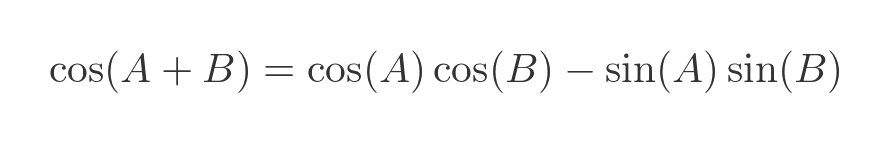
Once again, we substitute the real part x for A, and the imaginary part iy for B:

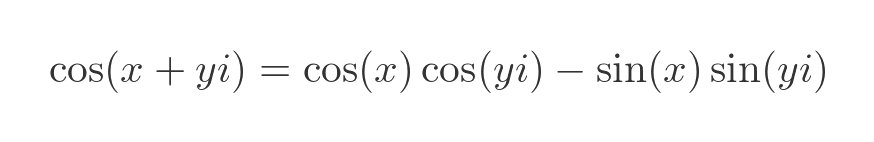
And converting the imaginary terms to hyperbolic functions:

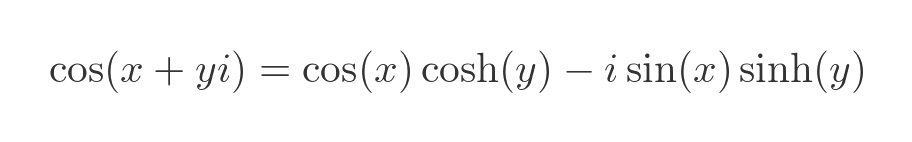
Here is a colour map:

Here is a 3d graph:

Complex tangent

We can do similar things for the other trigonometric functions. We won't cover them all, but as an illustration here is how we find the tangent of a complex number. First, we will find an expression for the tangent of an imaginary number. For the definition of tan:

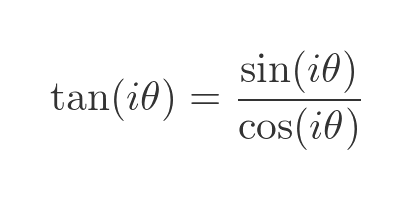
If we substitute the imaginary sine and cosine with the hyperbolic functions, just like before, we can find the tangent in terms of the hyperbolic tangent:

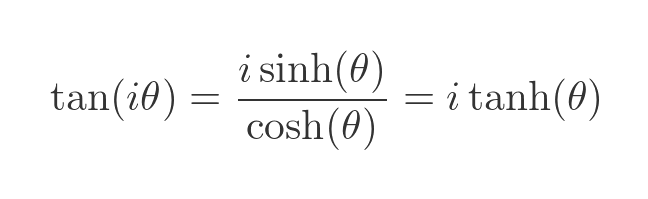
This result is, perhaps, not too surprising. Next, we will use the standard formula for the tangent of the sum of two angles:

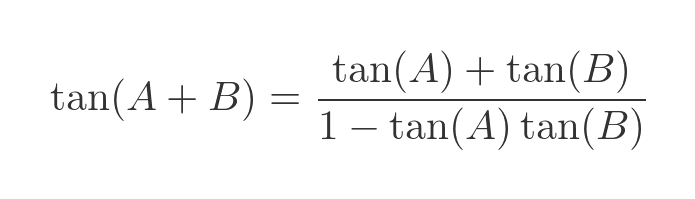
As before we apply this to the real and imaginary parts of x + yi:

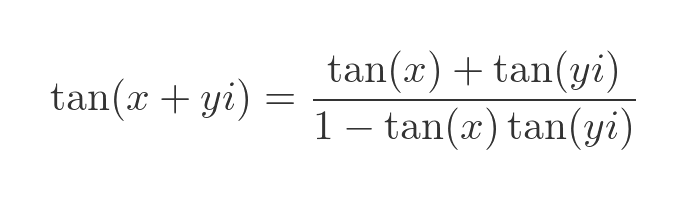
Finally, substituting the hyperbolic tangent for the tangent of iy gives us a formula for the tangent of a complex number:

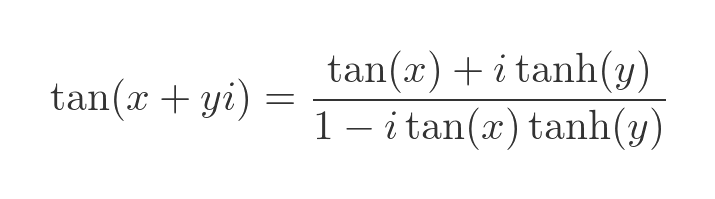
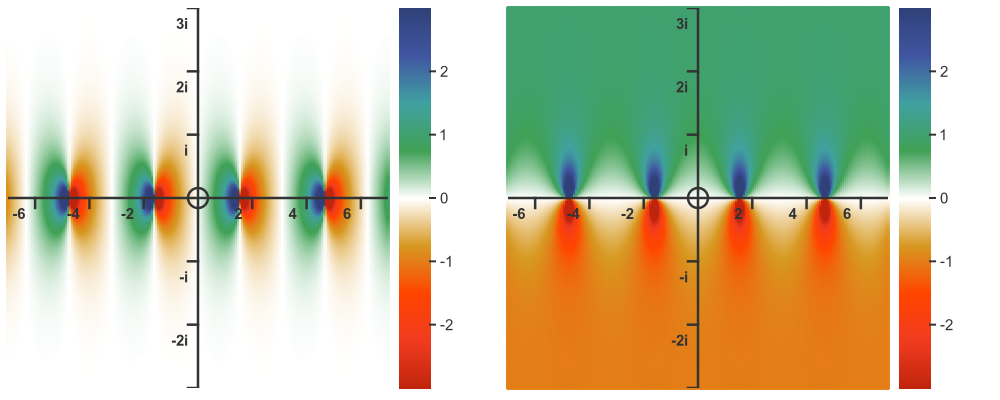
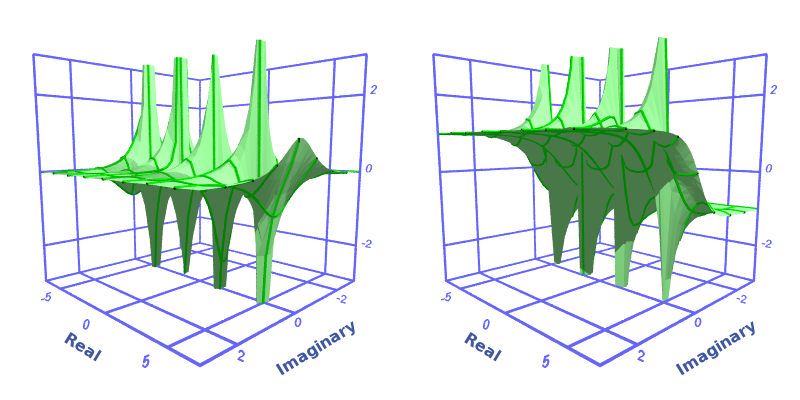
Here is the colour map and 3d graph:

See also

• Imaginary and complex numbers
• Complex number arithmetic
• Argand diagrams
• Why does complex number multiplication cause rotation?
• Modulus-argument form of complex numbers
• De Moivre's theorem
• i to the power i
• Euler's formula - proof
• Complex powers and roots of complex numbers
• Semiprocal numbers - z to the power i
• Complex polynomials