De Moivre's theorem

De Moivre's theorem can be simply stated as:

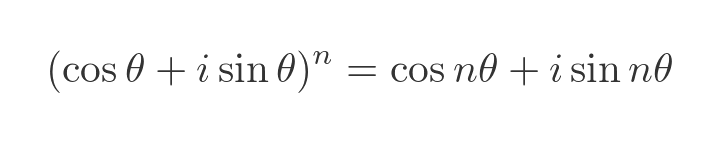
Notice that the sine function on both sides is multiplied by the imaginary unit i. This isn't a pure trigonometrical identity, instead it is a formula that applies to complex numbers.

This formula is an early precursor to Euler's identity. It is easier to prove - it derives directly from the definition of complex multiplication - but it is not as versatile.

Complex multiplication

When we first learn about complex multiplication, we simply apply the FOIL rule. For example, if we multiply 1 + i (which we will call a) and 1 + 4i (which we will call b), we get the result c, which is -3 + 5i:

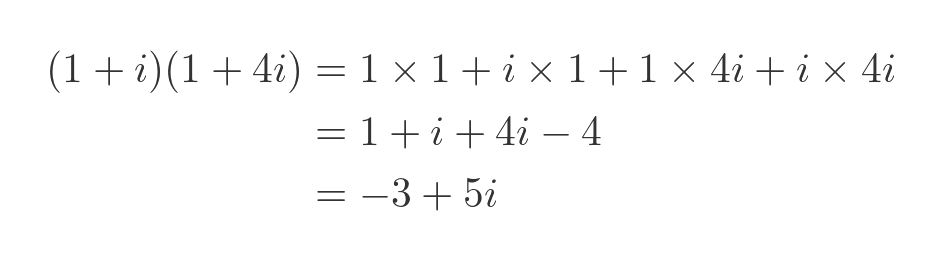
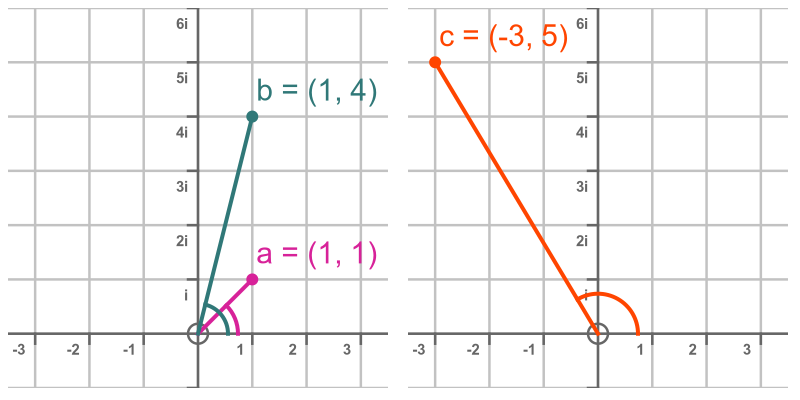
This is shown here on an Argand diagram:

Modulus argument form

A complex number can be represented in the form x + iy, but it can also be represented in modulus argument form. In that case, we define the complex number using the angle Θ that the number makes with the real axis, and the length r from the number to the origin. This diagram shows the two alternative ways of representing the same complex number:

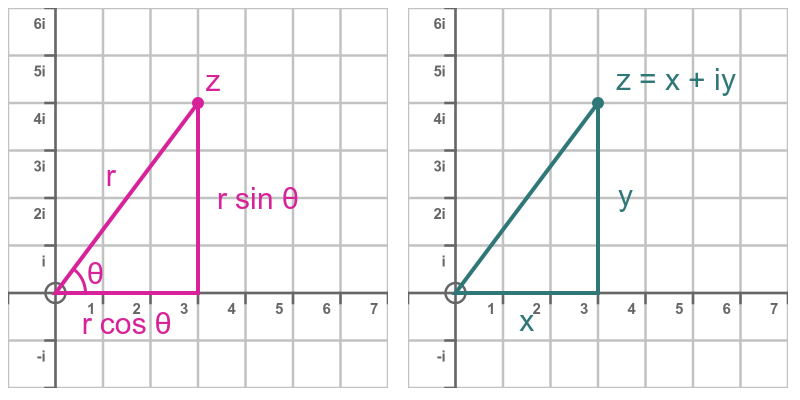
If we know x and y, we can find the angle Θ by basic trigonometry:

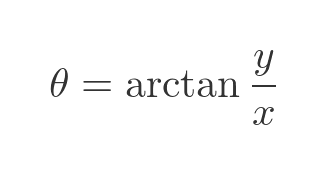
We can use this to calculate the angle Θ for the numbers a, b and c from the previous section:

Remember, of course, that c is equal to a times b, which we multiplied out longhand using FOIL. The interesting thing to notice here is that the angle of c is equal to the sum of the angles of a and b. In other words, when we multiply a by b, it has the effect of rotating a through the angle of b. This rule is true in all cases and is covered in the article Why complex multiplication causes rotation.

We can also calculate r if we know x and y. This just uses Pythagoras' theorem:

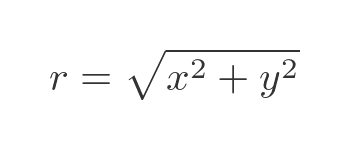
We can calculate r for all three of our complex numbers:

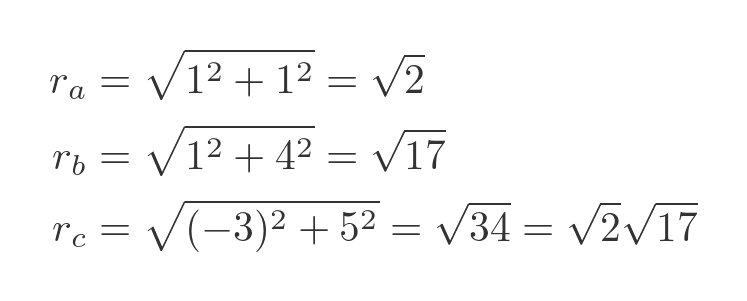
This shows that the modulus of a multiplied by b is equal to the product of the two moduli. Again, this rule is true in all cases.

So, in summary, when we multiply two complex numbers expressed in modulus argument form, we add the angles and multiply the lengths.

Graphical explanation of De Moivre's theorem

De Moivre's theorem is based on a complex number defined like this, which we will call m:

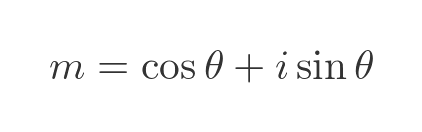
Comparing this with the modulus argument form of complex numbers, we can see that any complex number with this form has a modulus of 1 and an argument of Θ. This means that every complex number of this form is on the unit circle on an Argand diagram:

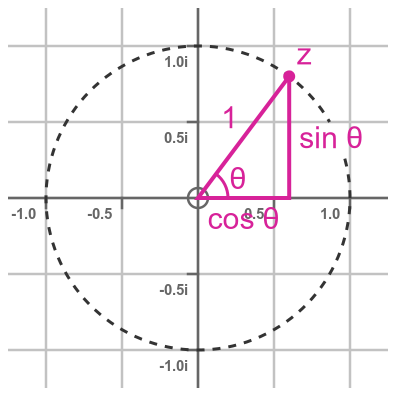
De Moivre's theorem applies to integer powers of complex numbers that take the form of m. Let's start by looking at m squared. From the last section we know that when we multiply two complex numbers expressed in modulus argument form, we multiply the moduli (r values) and add the arguments (Θ values). But m has a modulus of 1, so m squared will also have a modulus of 1. So we only need to deal with the angles.

Here is m squared, which we can be expressed as m times m:

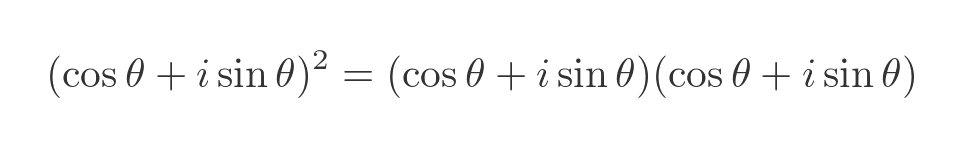
When we multiply two numbers, we add the angles:

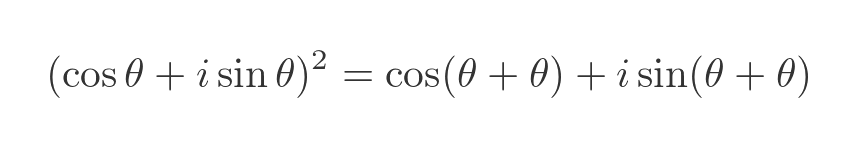
And we can express Θ + Θ as 2Θ:

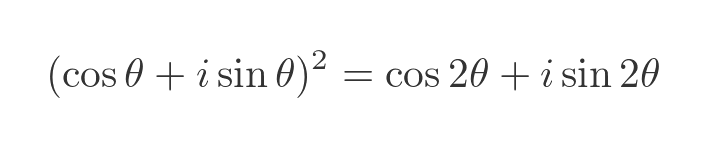
So multiplying m by m doubles the Θ, exactly as De Moivre's theorem states. Here are m and m squared on an Argand diagram:

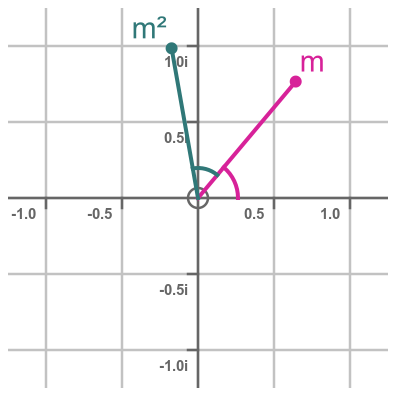
Let's try the same thing with m cubed. This can be expressed as m times m squared. This adds another Θ to the angle, bringing it to 3Θ, again as predicted by De Moivre:

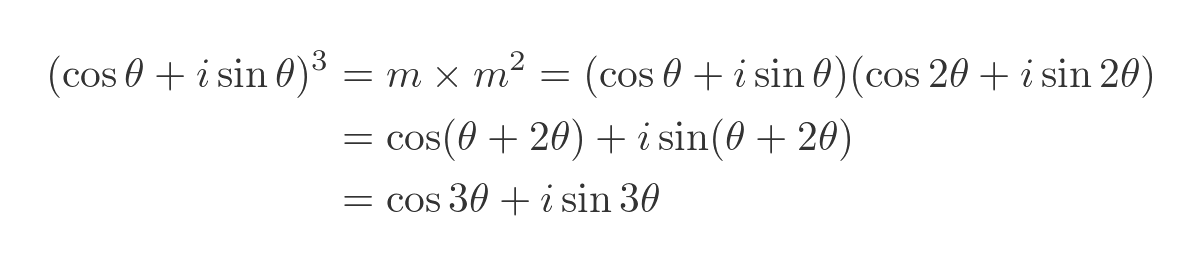
Here is m cubed vs m squared on an Argand diagram:

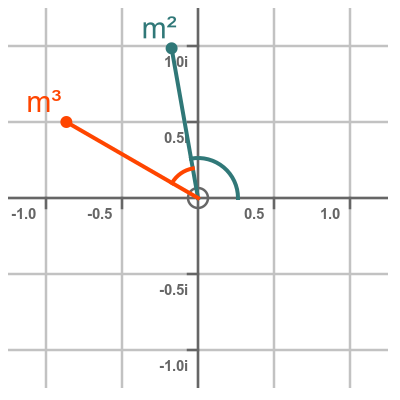
m squared makes an angle 2Θ with the real axis, and m cubed makes an angle 3Θ.

Proof by induction

A good way to prove this theorem is proof by induction. This type of proof has two steps:

1. First we prove that, if the theorem is true for some integer k, it must also be true for k + 1.
2. Then we prove that it is true for the value 1.

Since it is true for n = 1, step 1 tells us it must also be true for n = 2. This means it must also be true for n = 3, and so on. So it is true for all n.

This proof applies to all positive n. It is not too difficult to extend this proof to negative n, but we won't cover that here, we will just prove the result for positive n.

Step 2 is the easiest, so let's get that out of the way first. We want to prove this equation when n is 1:

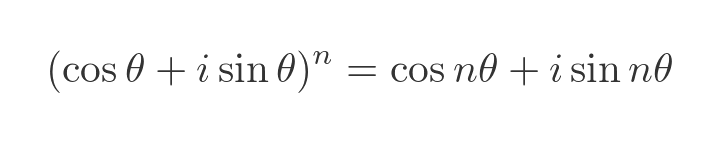
If we substitute n with 1, we get this:

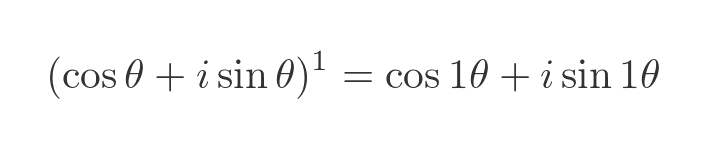
Taking the LHS, we know that x raised to the power 1 is simply x, so we have this:

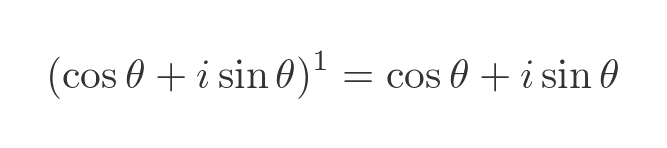
Taking the RHS, for any function f we know that f(1x) is equal to f(x) so we have:

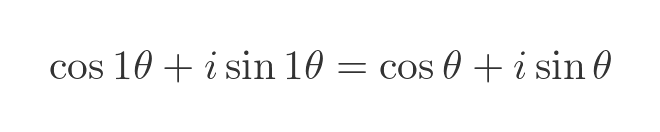
This shows the LHS and RHS of the original equation are equal, which proves that De Moivre's theorem is true for n equals 1.

Next, we wish to prove that, if the theorem is true for k then it is also true for k + 1. We can start with a basic rule of exponentials, that x to the power (k + 1) is equal to x to the power k times x. Applying this to De Moivre gives us:

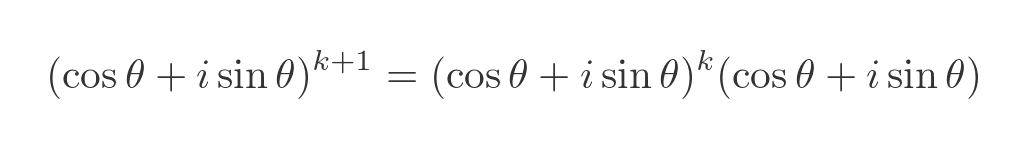
Remember that we are assuming De Moivre is true for k. This means we can apply De Moivre to the first term on the RHS. This gives us:

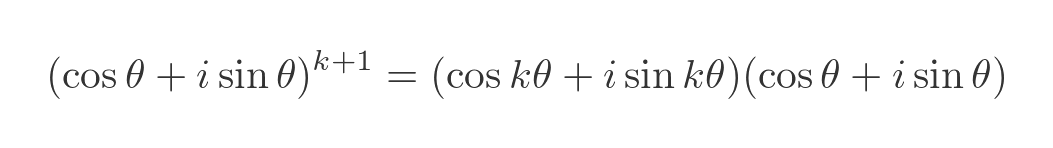
We can multiply out the RHS and gather the real and imaginary terms:

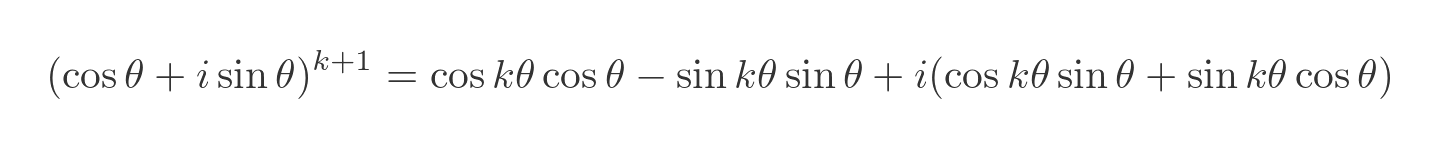
The real part of this corresponds to a well-known trig identity:

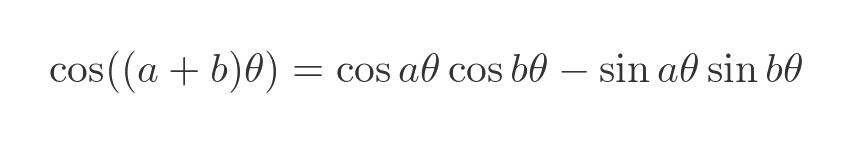
Substituting k for a, and 1 for b gives us an alternative form for the real part of our formula:

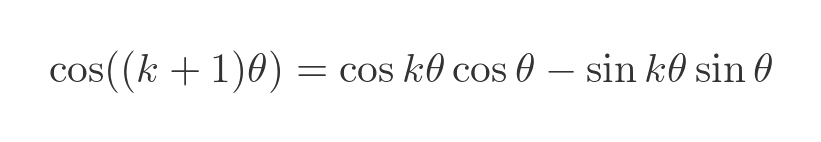
The imaginary part corresponds to another well-known trig identity, so we can do a similar thing:

Here is our formula again:

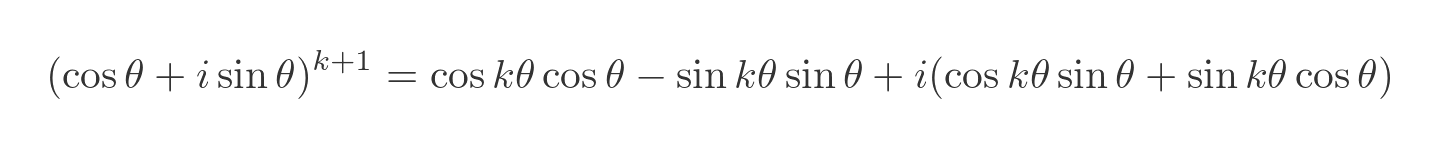
If we apply the two trig identities, we get:

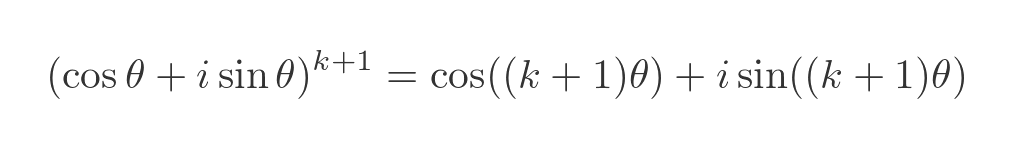
This proves that if De Moivre's theorem is true for k it is also true for k + 1. And since we have already proved that it is true for 1, this proves it is also true for all positive integers k.

Integer roots using De Moivre's theorem

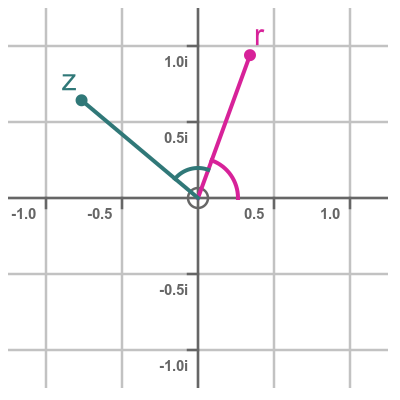
Here are two complex numbers r and z, each with unit modulus, where z is r squared:

Of course, since z is r squared, it follows that the angle of z is twice the angle of r:

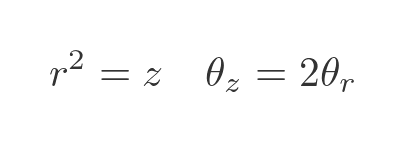
We can rewrite this in terms of z. In that case, r is the square root of z, and also the angle of r is half the angle of z:

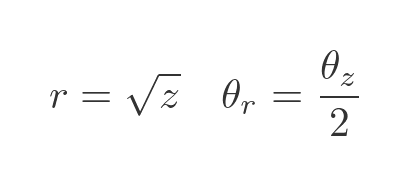
We can generalise this to the case where z is r to the power n, meaning that r is the nth root of z. In that case the angle of r would be the angle of z divided by n:

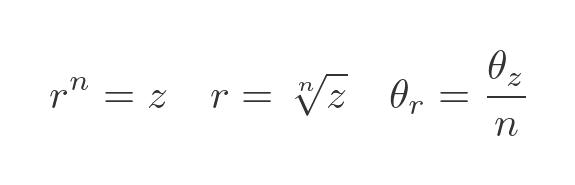
This gives us a new variant of the De Moivre formula, for finding the nth root of a complex number:

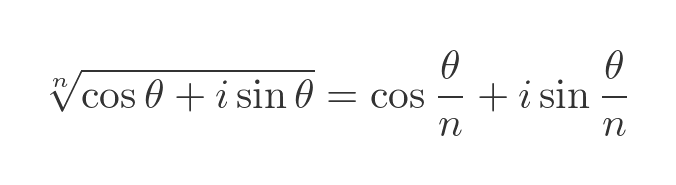
It is worth remembering, though, that this only finds one root of the number. In general, when we find the nth root of a complex number (where n is a positive integer, and the complex number is not zero) we would expect n distinct values. This is discussed in the article on complex powers and roots.

Comparison with Euler's formula

You may be familiar with Euler's formula, which looks like this:

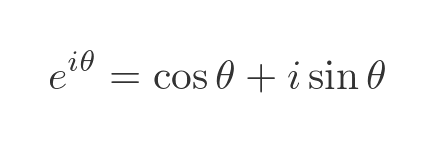
You might notice a similarity with De Moivre's formula. That is because De Moivre's theorem is a simpler form of Euler's formula, discovered earlier. In fact, it is quite easy to prove De Moivre's theorem from Euler's formula. First, let's raise both sides to the power n:

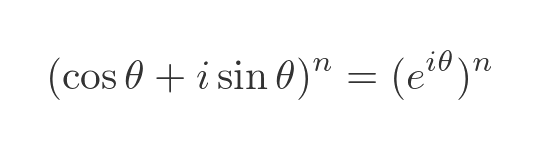
We can then bring the n inside the exponential:

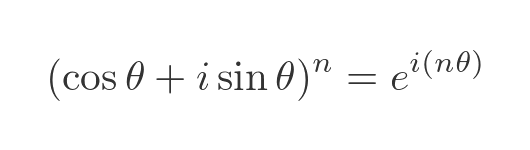
We now have a new exponential expression - this time it is e to the power i times nΘ. We can apply Euler's formula again, this time using nΘ instead of Θ:

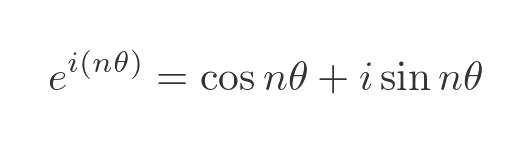
Combining the two previous equations gives us De Moivre's theorem:

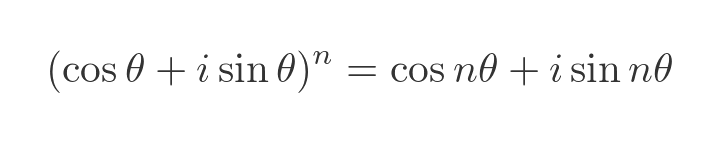
Euler's formula needs several articles to itself, but for now, it is worth saying it provides a rich superset of the properties of De Moivre's theorem. While De Moivre is limited to raising complex numbers to integer powers, Euler's formula allows us to:

• Raise a complex number to any real power, including fractional or irrational powers.
• Raise a complex number to a complex power.
• Find any root of a complex number to any real power, including fractional or irrational roots.
• Find a complex root of a complex number.
• Find all the roots, not just the primary root.

However, Euler's formula is slightly more difficult to understand, and a little more tricky to prove. It is worth understanding De Moivre's theorem before moving on to Euler's formula.

See also

• Imaginary and complex numbers
• Complex number arithmetic
• Argand diagrams
• Why does complex number multiplication cause rotation?
• Modulus-argument form of complex numbers
• i to the power i
• Euler's formula - proof
• Complex powers and roots of complex numbers
• Semiprocal numbers - z to the power i
• Complex polynomials
• Complex number trigonometry functions