Integration by parts - LIATE rule

The technique of integration by parts can often be used for solving complex integrals, particularly if we need to integrate a function that can be expressed as the product of two other functions.

The basic integration by parts formula is:

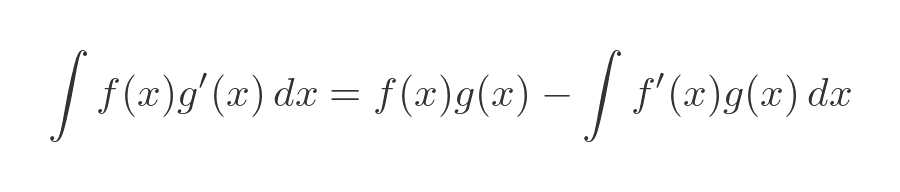
However, it can sometimes be difficult to decide how best to proceed.

The LIATE rule is a simple rule of thumb to help with this. It isn't foolproof, so we should always be prepared to try a different route if the LIATE rule doesn't give a good result. Indeed, there is not even consensus on the order of the rule, and some people use the ILATE rule (the slight difference will become clear soon).

Also, of course, the LIATE rule only covers certain classes of functions. These include all the very common mathematical functions, but if we ever need to integrate an expression involving other types of functions, the rule won't directly help us. But we can still apply the principles of these rules to other function types.

In this article, we will explain the rule and give an example of each of the cases.

The LIATE rule

The LIATE rule recognises five main types of function that commonly occur in integration problems:

Mnemonic	Function type	Example
L	Logarithmic	ln(x)
I	Inverse trigonometric	arcsin(x)
A	Algebraic	x²
T	Trigonometric	sin(x)
E	Exponential	exp(x)

If we are trying to integrate the product of two functions s and t, there are two possible ways to do it:

• We could substitute s for f, and t for g'. If we do that, the integration by parts rule will require us to differentiate s (to find f'), and to integrate t (to find g).
• Alternatively, we could substitute t for f, and s for g'. If we do that, the integration by parts rule will require us to differentiate t (to find f') and to integrate s (to find g).

Which should we choose? Of course, it depends on the functions s and t. Firstly, if either s or t is difficult to integrate, then we should not use that function for g'. This is the reason for the first two rules. Logarithmic functions and inverse trig functions are difficult to integrate so we should try to use these functions as f wherever possible.

Trig and exponential functions have a slightly different problem. They are fairly easy to either integrate or differentiate, but the result of either process is no simpler than the original. For example, if we differentiate the sine function, we get the cosine function. If we integrate sine, we get the negative cosine. Neither of those transformations is likely to make the equation any easier. So in that case we might as well use that function as g' so we integrate it. Then there is a chance that the other function might become simpler when we differentiate it.

Logarithmic functions

If one of the two functions is logarithmic, LIATE suggests we should try making that the first function, f. So to solve this integral:

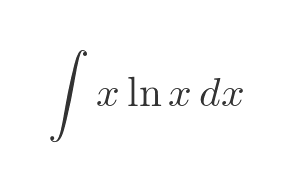
We should choose f and g' in this order (rather than the other way round):

Integration by parts requires us to also know f' and g. We can find f' by differentiating f. The derivative of ln is a standard result:

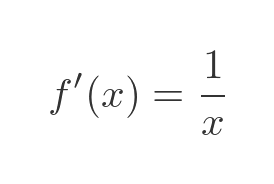
We can find g because it is the indefinite integral of g'. That is to say, if we differentiate the following function g we will get g':

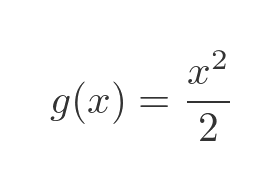
If we plug our values of f, g, f' and g' into the indefinite integral formula:

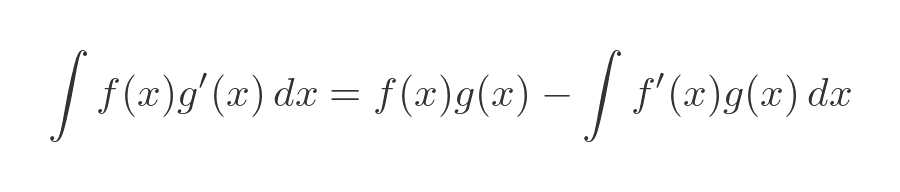
We get this result:

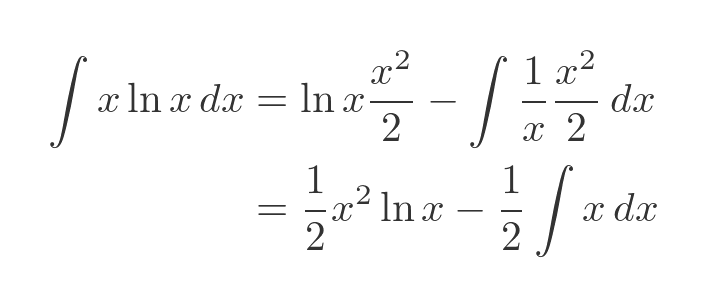
The integral term can be solved easily as it is a standard result:

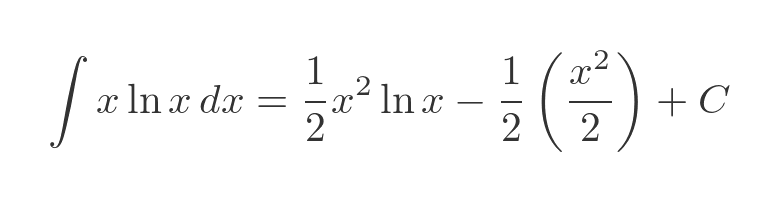
This simplifies to:

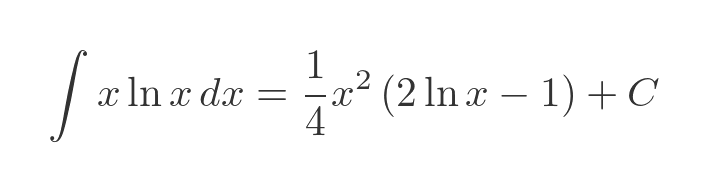
Here is a graph of the original function on the left, and the integral on the right:

Inverse trigonometric functions

Inverse trig functions are a little tricky to integrate anyway, so we will pick a simple example. We will integrate the inverse cosine function multiplied by 1. This is quite a useful trick in itself because it converts a difficult integral into a differentiation problem.

So, we want to integrate this:

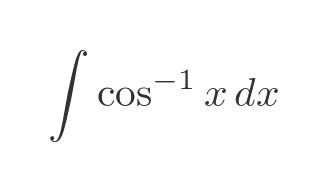
We will take the inverse cosine as f, and the implied multiplication by 1 as g':

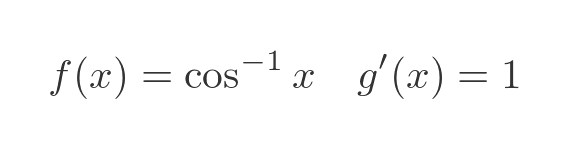
The derivative of the inverse cosine is a standard result:

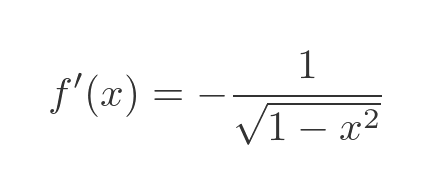
The indefinite integral of 1 is x:

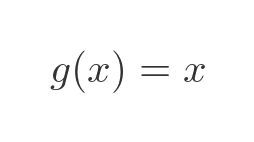
If we substitute all these values into the integration by parts formula and cancel out the double negative we get:

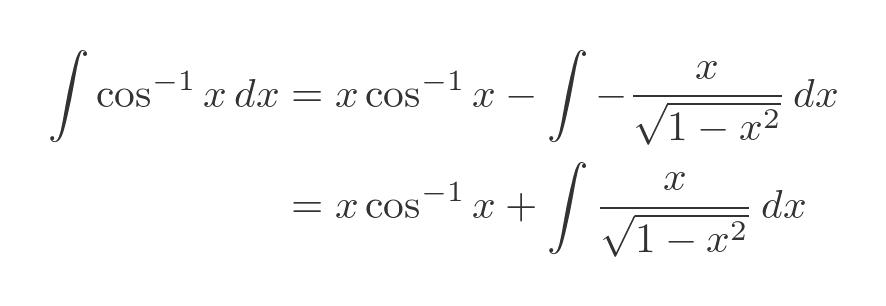
We will solve the integral using substitution. The following substitution simplifies the denominator of the integral term:

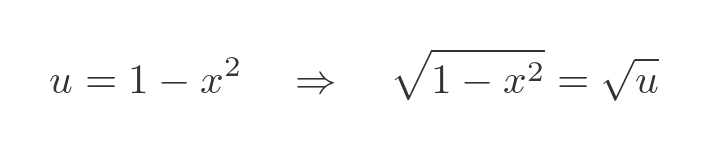
And, serendipitously, the x dx term is simplified when written as du:

Making these substitutions gives us a much simpler integral:

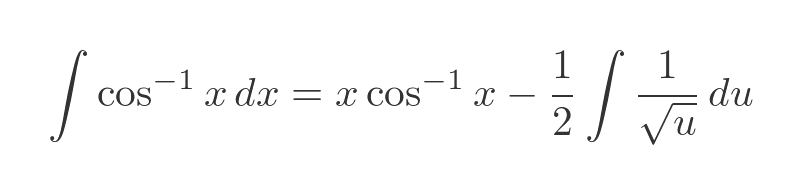
Now the reciprocal of the square root is equivalent to u to the power -1/2, so it can be integrated by the power rule:

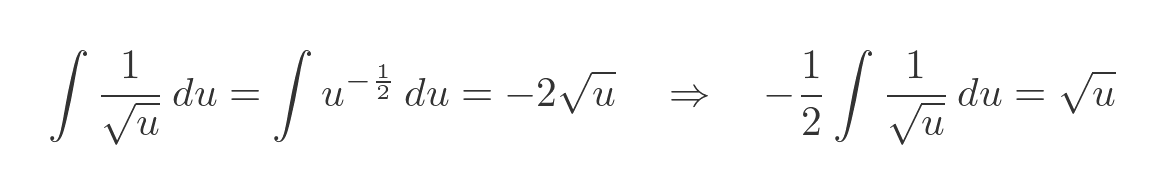
We can replace the integral term, and then substitute u with x to solve the integral:

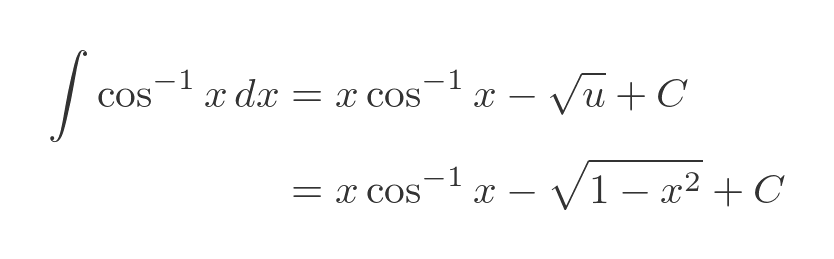
Here is a graph of the original function and its integral, remembering of course that the inverse cosine is only valid for values -1 to 1:

Algebraic functions

Algebraic functions are fairly easy to integrate or differentiate, so it is not surprising they sit in the middle of the list. When we had an algebraic function combined with a log function, we decided to integrate the algebraic function because that was easier. But now consider this equation:

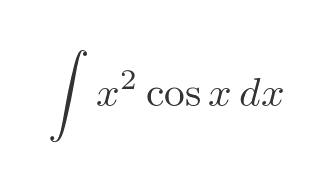
We are happy to either integrate or differentiate x squared. What about the other function, cos? That is also easy to integrate or differentiate, we just get sin, give to take a negative sign.

So which way should we go? And does it even matter?

Well yes, it matters quite a lot. The thing is, when we differentiate or integrate the cosine function, the resulting sine function doesn't really get us any further. Sine is not any simpler than cosine, and it isn't any more complex either. But if we integrate the x squared function, we get an x cubed function. That is a step in the wrong direction!

We definitely want to differentiate the x squared term. So let's define f and g' like this:

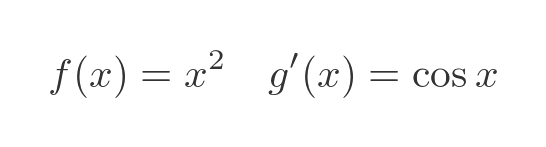
This gives us our simpler form for f':

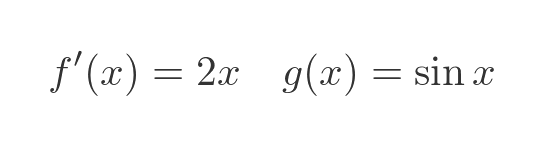
Putting these into the integration by parts formula gives:

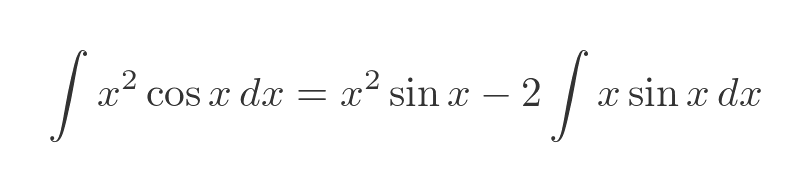
We now need to find the integral of x sin(x). You might notice that it is quite similar to the original problem. But, importantly, it is a slightly simpler version of the original problem. We won't go through the details here, but we can solve it in the same way, giving this result:

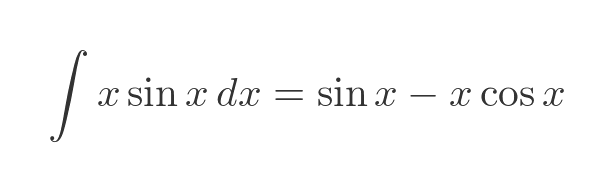
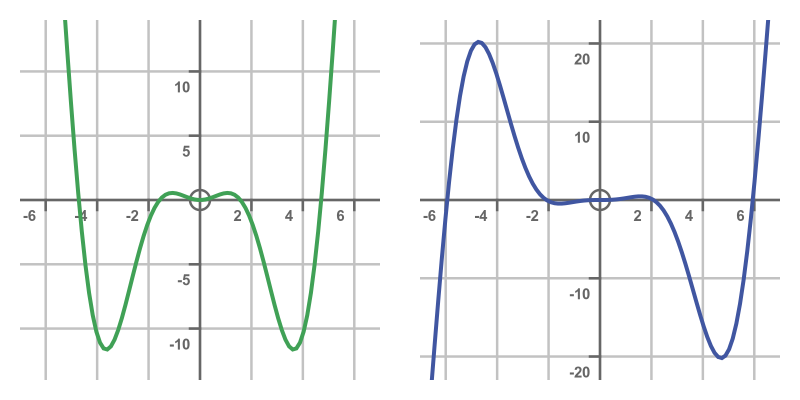
Putting this back into the previous formula and simplifying gives:

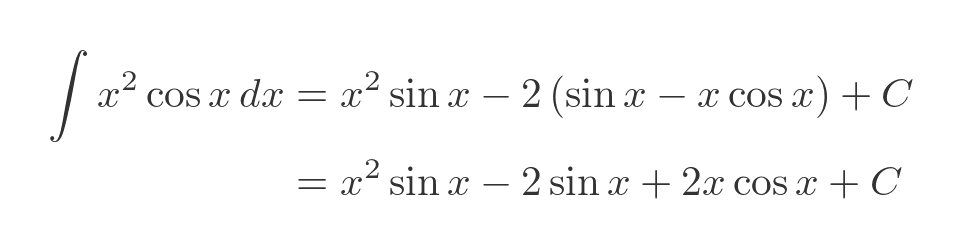
Here is a graph of the original function and its integral:

Trigonometric functions

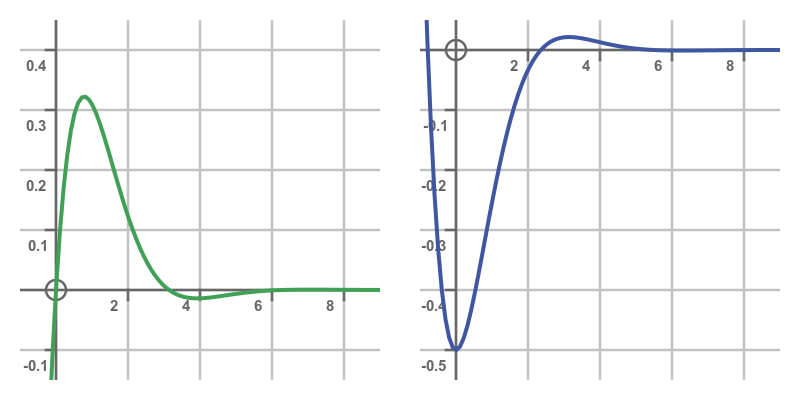
Since trigonometric functions are second from last in the LIATE list, the only time the rule will suggest them is if the other function is an exponential function. An example of this is a damped sine wave (that is, a sine function multiplied by an exponential function with a negative exponent). Here is such a function:

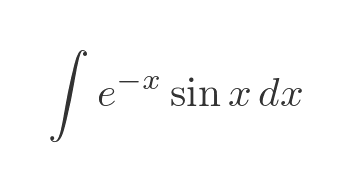
Now we might perhaps feel a little uneasy at this point. We know that integrating or differentiating sine will just give us cosine in some form. And integrating or differentiation an exponential will just give us another exponential. So won't we end up going round in circles? Let's see how it goes. Here are f and g':

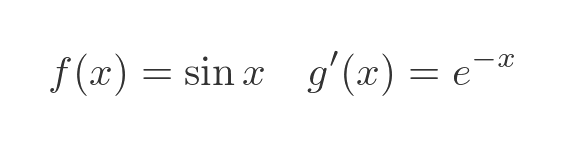
Here are f' and g. Notice that g is negative. That is because the exponential has a negative argument (this can be shown via simple substitution, we won't expand on it here):

Placing these terms into the integration by parts formula, and cancelling the double negative, gives:

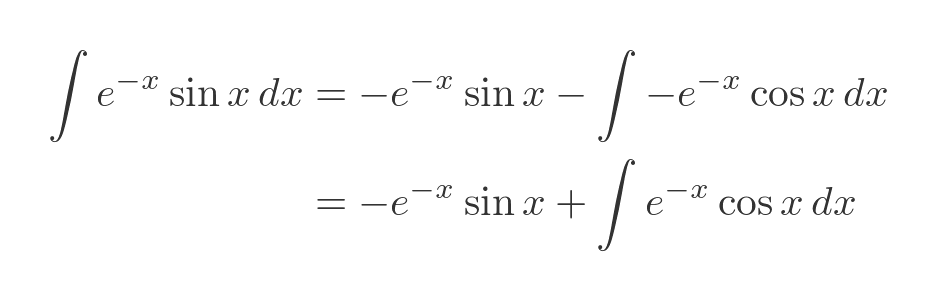
The integral term here is very similar to the original, it just has cosine instead of sine. We can solve it in the same way, and skipping over the details we get this:

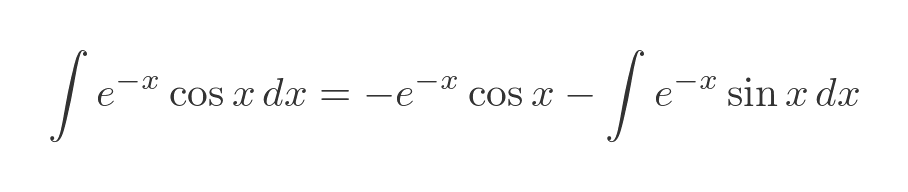
As we feared, we have come full circle and now need a solution to the original equation. But all is not lost. We can rearrange this to bring the original integral to the LHS:

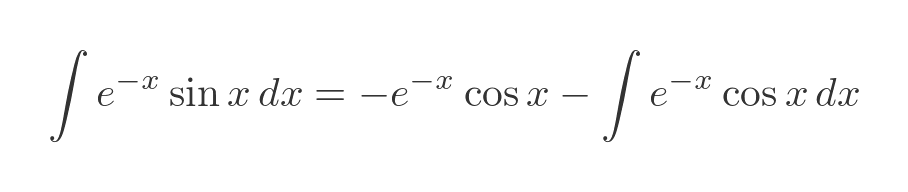
Compare this to the previous result:

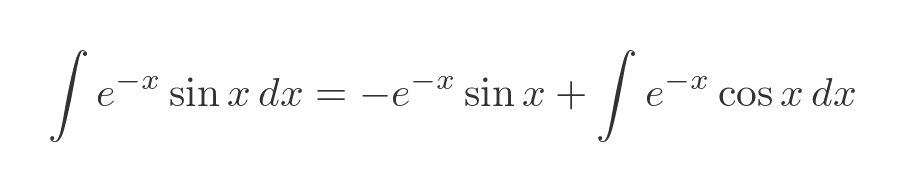
If we add these two formulas together the two cosine integrals cancel out:

Simplifying gives us a solution:

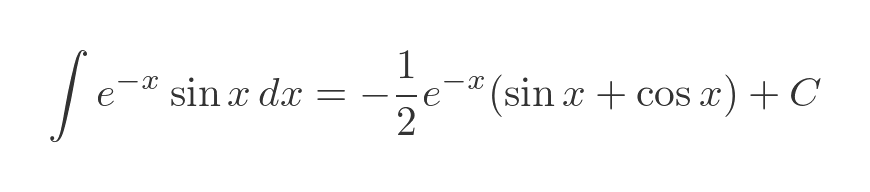
Here are the graphs:

Exponential functions

Each of our previous examples shows a case where that particular class was used as f, with the other function serving as g'.

Since exponential functions are the final class, we can't really give an example of this, because the LIATE rule would never choose to use an exponential function as f, it would always choose the other function.

What if both functions are exponentials? Like this:

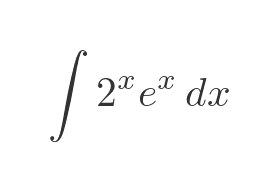
We could try using integration by parts, just as an exercise. But unfortunately, that won't get us anywhere. Integrating or differentiating either of the exponential functions won't result in any kind of simplification. It won't even result in a change of sign, which allowed us to solve the trig integral earlier. We will just end up needing to solve the exact integral.

Of course, we don't need to use integration by parts at all. This integral is easily solved by combining the exponentials before integrating, which gives a standard integral:

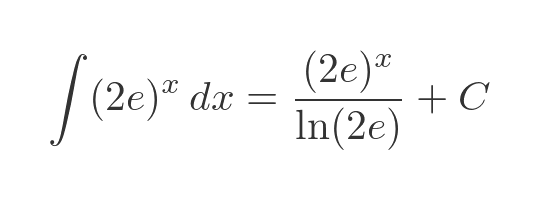
There is a good reason exponential functions are the last items on the LIATE list.

See also

• What is integration
• Integration by substitution
• Mean value theorem for integrals
• Fundamental theorem of calculus
• Improper integrals
• Integration by parts
• Finding arc length by integration
• Volume of revolution
• Gabriel's horn