Improper integrals

A definite integral is an integral between two finite points a and b:

We normally expect f to be continuous and bounded over the interval [a, b].

It is sometimes possible to break these conditions. Integrals that break these conditions are called improper integrals, but in some cases it is quite possible to calculate the area under the curve. Here are three examples:

The first is:

This integral extends to infinity, but as x tends to infinity, the function tends to zero, and we will show that the area under the curve converges to a finite value.

The second is:

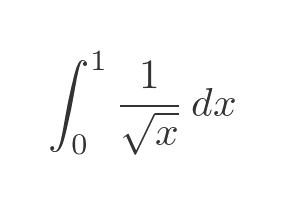
This integral is from 0 to 1, but as x tends to zero, the function tends to infinity. This is different to the previous case, because x is finite and f(x) tends to infinity, but once again we will see that the area is finite.

The final integral is:

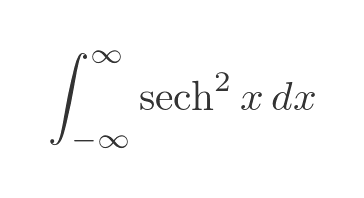
This integral goes from minus infinity to infinity. As x tends to infinity in either direction, the function tends to zero, and again we will show that the area under the curve converges to a finite value.

Improper integrals from a to infinity

Let's consider the first function above:

This is quite a straightforward integral, except for the limit values. It is a standard integral (notice that because the exponent is negative, the integral becomes negative - this is a trivial application of integration by substitution):

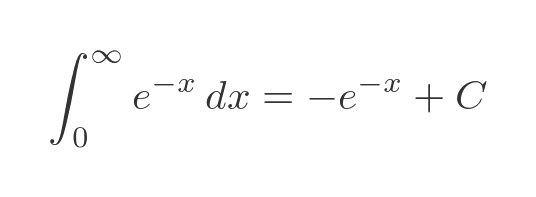
How do we handle the infinite limit? Well, we can simply evaluate the definite integral in the normal way:

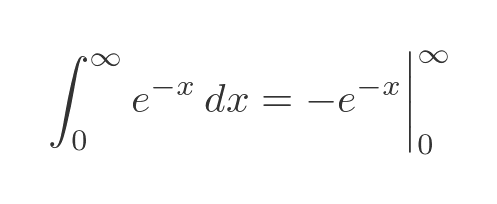
Evaluating at zero, since we know anything raised to the power 0 is 1, gives:

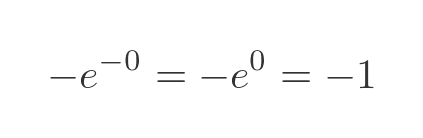
Evaluating at infinity gives:

So the result is 0 -(-1), which is 1.

We evaluate an improper integral in the same way that we evaluate a normal integral. If the result is finite, it means that the curve encloses a finite area. We say that the integral converges.

Not all functions converge

There is no guarantee that the area will be finite. For example, these three functions don't converge for various reasons.

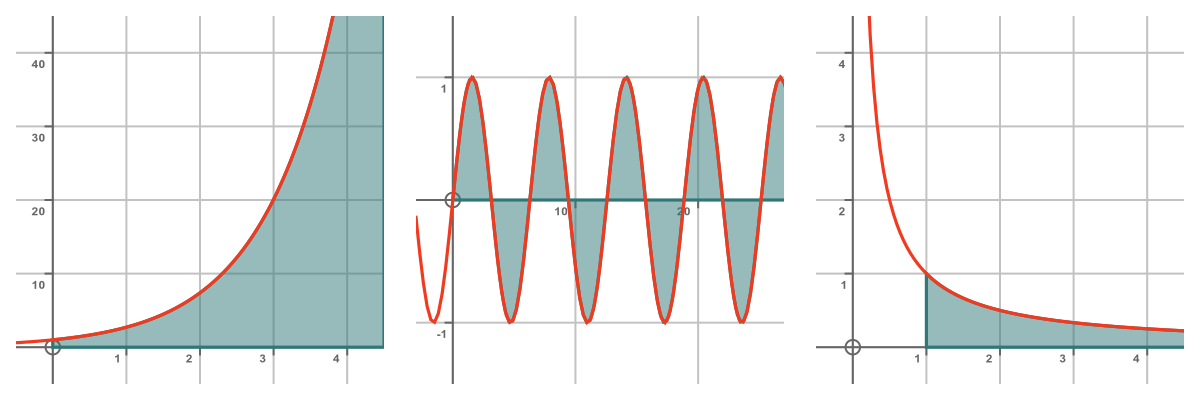
The first function is:

The exponential function, of course, increases as x increases, without bounds. Therefore we cannot come up with any useful value for the area under the curve as x tends to infinity. It is just an infinite area.

The second function is sin x. This doesn't converge for a different reason. The sine function, of course, oscillates around the x-axis. Starting from zero, the function is first positive, so the area under the curve increases. The function then goes negative, which contributes a negative area to the total. By the time we reach x = 2π the positive and negative areas cancel out exactly. Then the cycle repeats, over and over.

As x gets very large, the situation doesn't change. The area under the function varies up and down but never settles on a value. We can't say what the area under the sine function is at infinity because there is no overall trend to the area, it just goes up and down forever. So it is impossible to solve the improper integral.

Finally, the graph on the RHS shows the function 1/x in the interval [1, ∞]. This function gets smaller and smaller as x gets bigger, just like our original decaying exponential function. Surely this integral should converge too?

Well, it turns out that it doesn't. Let's find out why. We need to find the integral:

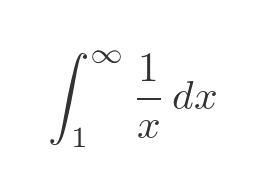
This is a standard integral, with an antiderivative ln|x| + C. Since we are dealing with positive values of x we don't need to worry about the modulus, so the definite integral is:

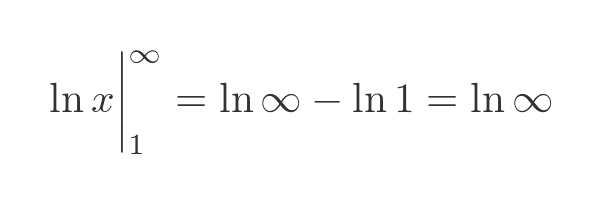
So, just like the exponential function, the ln function doesn't converge. The function is shown here:

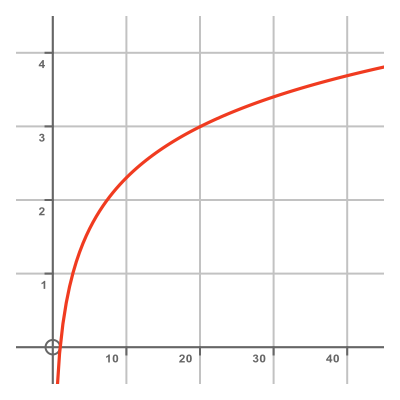
If we compare this to the exponential function, we see that the exponential function always increases, and the rate of increase gets faster as x gets bigger. By contrast, the log function always increases but the rate of increase gets slower as x increases. But that doesn't matter, the function is always increasing so its growth will be unbounded as x tends to infinity.

If we try the same thing using the function 1/x² rather than 1/x, the integral converges and the area under the curve is finite (try it if you wish!).

If the value of f(x) tends to zero as x tends to infinity, that is not enough to guarantee that the area under the curve will be finite. It depends on the value of the integral at infinity.

Improper integrals with an asymptote on a boundary

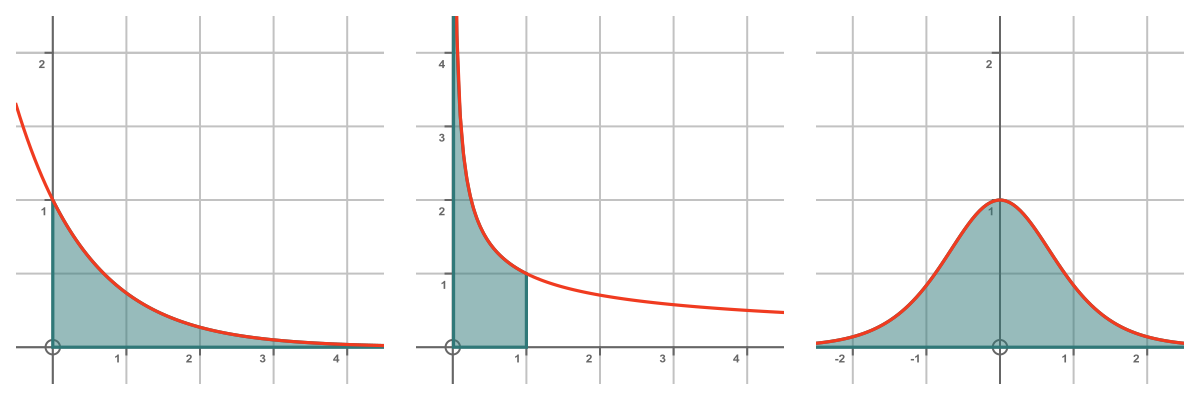
Suppose we wanted to find the area under the curve 1/√x but over the interval [0, 1]. This is shown on the left here:

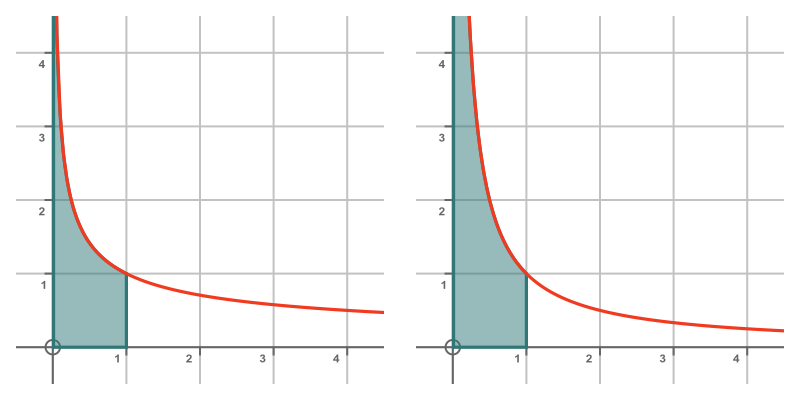
This is also an improper integral, but this time the range of x values is finite, but the value of f(x) goes to infinity at one boundary x = 0.

We tackle this in the same way as before - we integrate the function and find the definite integral by evaluating the integral at the boundaries. We can express the function as a power:

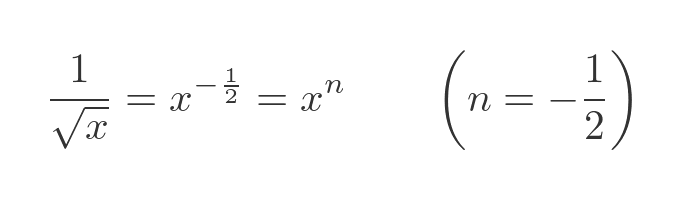
The antiderivative (ignoring the constant of integration) is:

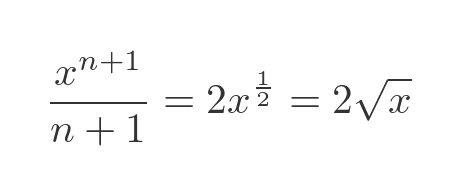
We can find the definite integral from 0 to 1:

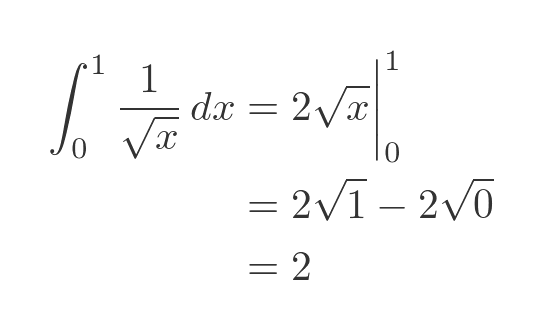
So the area under the curve is finite and is simply 2.

The RHS of the previous graph shows the function 1/x. We can calculate the area under this curve too, we have already done this calculation for [1, ∞], and here is the same calculation for [0, 1]. We will use the fact that \ln x goes to -∞ as x goes to zero:

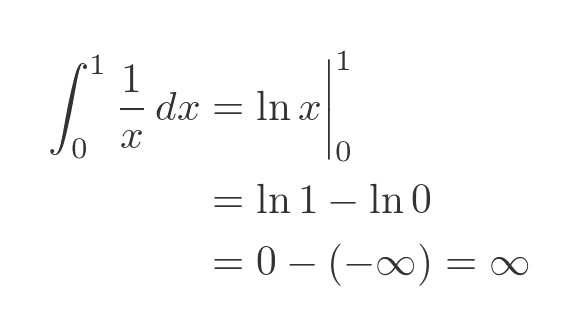
The two functions are very similar in shape. There is a subtle difference - if you notice, the 1/x curve approaches the y-axis slightly more slowly as x decreases towards zero. This small difference has a profound effect.

The area under 1/√x is finite, but the area under 1/x is infinite. You can't really guess whether an improper integral converges just by looking at the curve!

Improper integrals over interval [-∞, ∞]

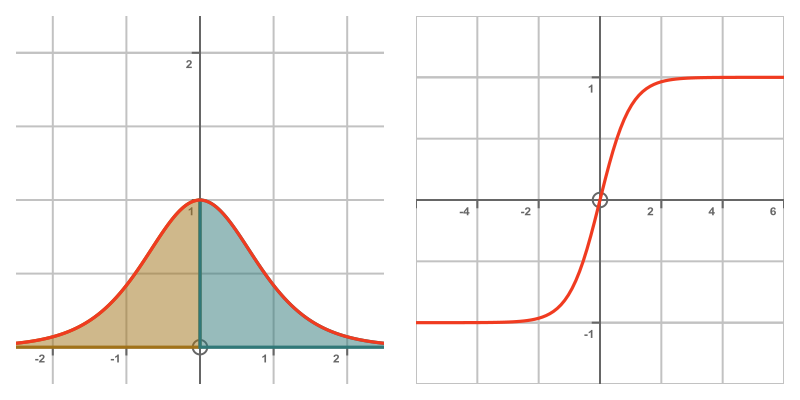
Our next example is the integral of sech squared, over the interval [-∞, ∞], shown on the LHS below:

We can't generally integrate between -∞ and ∞ in one operation. Instead, we need to split the integral into two parts:

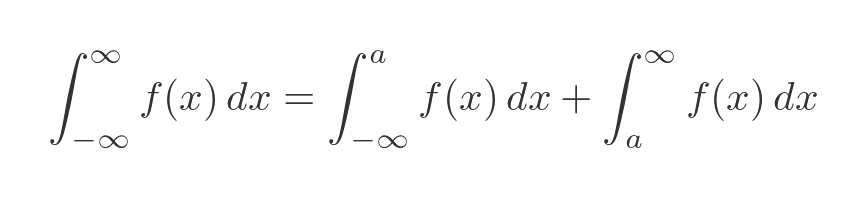
Where a is some finite intermediate value. Any value will work, but in this case, it is convenient to use zero because the function is symmetrical about the y-axis. This is shown in above, where the yellow and cyan shaded areas are equal due to this symmetry. So the total area is:

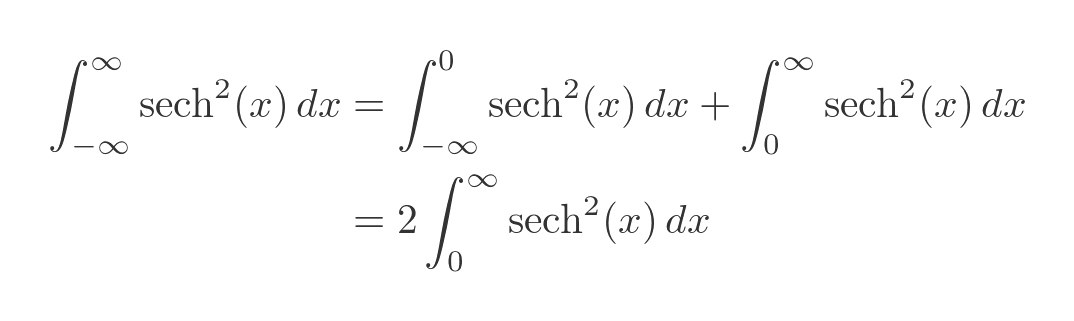
This is a standard integral, tanh x + C, so the integral becomes:

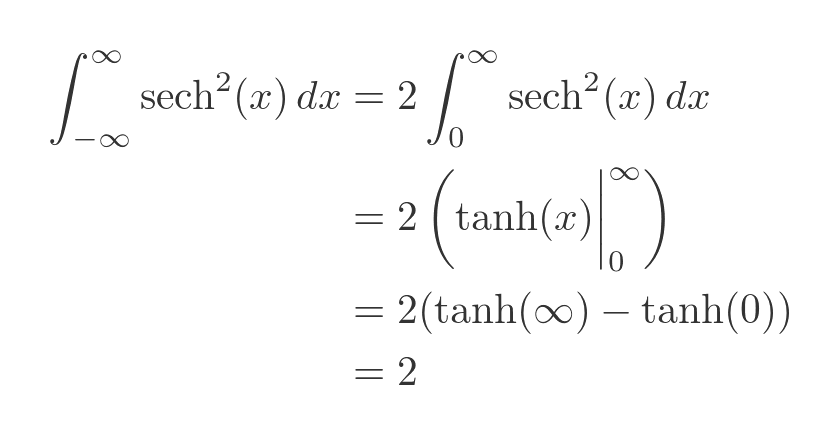
Here we have used the fact that tanh(0) is 0, and tanh(x) tends to 1 as x tends to infinity (shown on the RHS of the image above).

See also

• What is integration
• Integration by substitution
• Mean value theorem for integrals
• Fundamental theorem of calculus
• Integration by parts
• Integration by parts - LIATE rule
• Finding arc length by integration
• Volume of revolution
• Gabriel's horn