Koch snowflake

The Koch snowflake fractal is a variant of the Koch curve:

The outline of the snowflake of formed from 3 Koch curves arranged around an equilateral triangle:

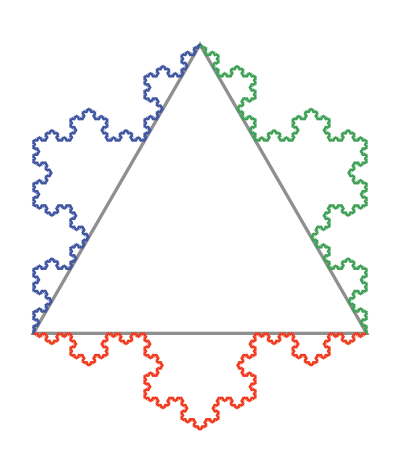
In this article, we will look at the properties of the Koch snowflake, and investigate several ways to construct the shape.

Constructing a Koch snowflake

To construct a snowflake, we start with an equilateral triangle:

We replace each side of the triangle with four lines, like this:

Each of the four lines is one-third of the length of the original side. The central spike forms an equilateral triangle, making an angle of 60° to the main line. If we do this to all three sides of the original triangle, we get this result:

This shape is a regular hexagram, which is a 6-pointed star with all sides equal length. If we divide each side again in the same way we get the shape on the left, below:

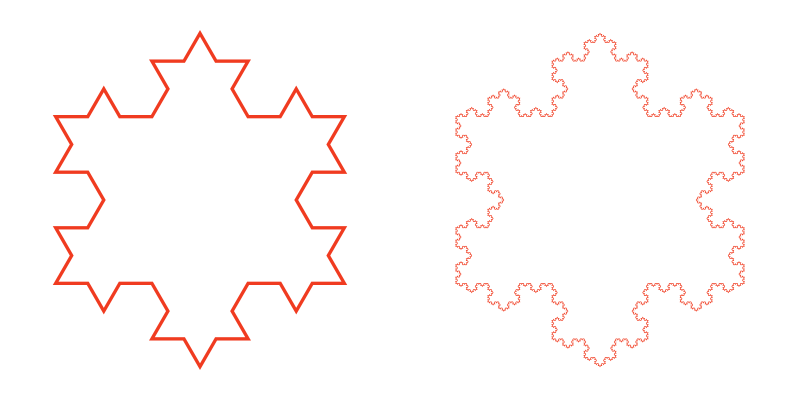
The shape on the right is formed by dividing each line a further three times. The shape is fractal in nature. We can keep dividing the sides forever.

Tessellation

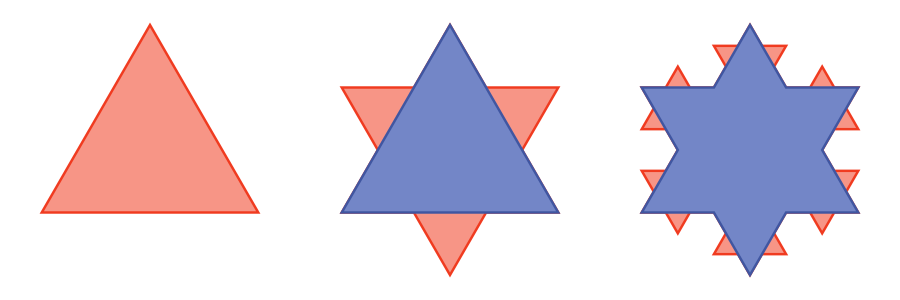
We can tessellate Koch snowflakes. Even though the edges are infinitely subdivided, they join together perfectly!

We can't tessellate two snowflakes of the same size, we need to use at least two different sizes (the ratio of linear dimensions must be equal to the square root of 3). Here is how the shapes join up:

All the larger red snowflakes are the same size, and all the smaller blue snowflakes are the same size. Despite the two types of snowflakes being different sizes the edges match up. This is due to the fractal nature of the shape. Note that if we approximate the fractal using a finite number of iterations, the edges will not quite match, although they will be very close if we use a large number of iterations. But for the edges to match exactly, we need to take the limit as the number of iterations goes to infinity.

Also, notice that each large red snowflake has six adjacent small blue snowflakes. The combination of the red shape and its six neighbours is also a (slightly larger) Koch snowflake. But those larger snowflakes don't form a tessellation because each blue snowflake is shared by three red snowflakes.

Iterated Function System

As we saw above, we can create a Koch snowflake from seven similar (but smaller) snowflakes, like this:

Assuming we start with a snowflake that is the exact size of the composite shape above (that is, all the red and blue shapes combined), then we can recreate the full snowflake by transforming the original seven times:

• Triangle 1 is created by scaling the original down by a factor of root 3, keeping its centre in the same place.
• Triangle 2 is created by scaling the original down by a factor of 3 and translating it down by a 1/3 (relative to the side length of the equilateral triangle that the snowflake is based on).
• Triangles 3 to 7 are similar to triangle 2, except they are translated in different directions. Each direction is a different multiple of 60° from the centre of the original triangle.

This set of seven transforms makes up an Iterated Function System (or IFS). The interesting thing about an IFS is that it is uniquely associated with a particular shape. Those seven particular transforms are associated with the Koch snowflake.

What do we mean by that? Well, we have just seen that if we take seven copies of the snowflake and transform them via the IFS they will exactly match the original snowflake. And we could repeat that, applying the transform again. The seven snowflakes would be transformed into 49 snowflakes, of different sizes, which taken together would exactly map onto the original.

But an IFS is weirder than that. If we take ANY shape and apply the IFS repeatedly, it will eventually map onto a Koch snowflake. Here is what happens if we start with a circle:

We start with a large circle, and add six smaller circles around the perimeter. We then add six even smaller circles around the perimeter of those circles (top right). Next we add even smaller circles around those (bottom left). The bottom right image shows the result after several more iterations. At this point the circles themselves are too small to be seen, and what remains is a good approximation to a Koch snowflake.

In a sense, the IFS, which is simply a set of transforms, actually defines the snowflake. We call the snowflake the strange attractor of the IFS.

Anti-snowflakes

The anti-snowflake is an interesting variant of the regular snowflake. It is formed in a similar way, but when we add the extra triangular section to each line, it points inward rather than outwards. Here is an anti-snowflake drawn with 0, 1, 2, and 5 iterations:

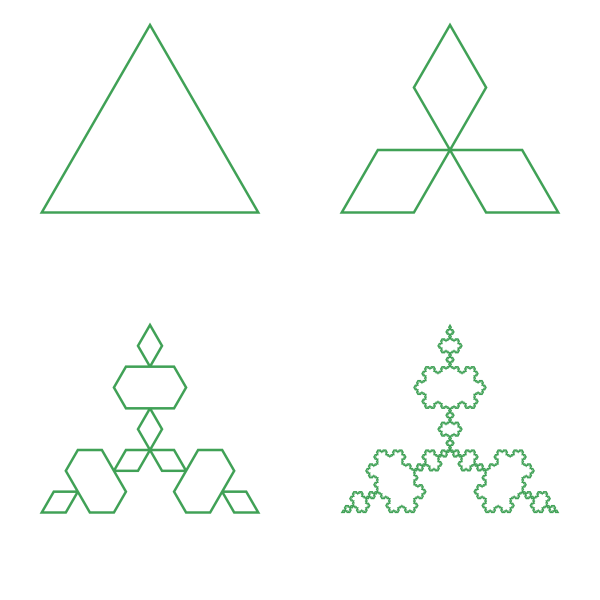
If we try to tessellate equal-sized snowflakes in a hexagonal pattern, we end up with gaps. It is perhaps not surprising that the gap where three snowflakes meet is an anti-snowflake:

Area of the Koch snowflake

Here are the first three stages of constructing a Koch snowflake:

The initial stage (iteration 0) is just an equilateral triangle, which of course has three sides.

On iteration 1, we draw a triangle on each side. This means that each side becomes 4 sides. So the second stage has 12 sides.

On iteration 2, we again draw a triangle on each of the 12 sides, so we then have 48 sides.

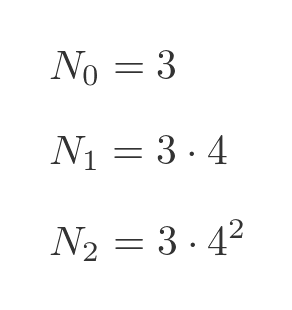
This pattern continues. The number of sides starts at 3 and then is multiplied by 4 on each iteration. So the total number of sides after iteration n is:

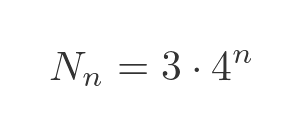
To calculate the total area of the shape, we first notice that each iteration adds extra triangles. The number of extra triangles added on iteration n (which we will call tn) is equal to the previous number of sides:

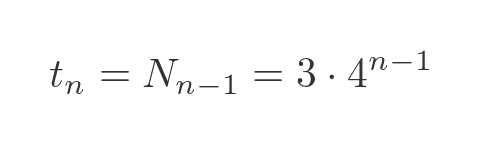
It will be convenient later if we express this in terms of power n, by multiplying top and bottom by 4:

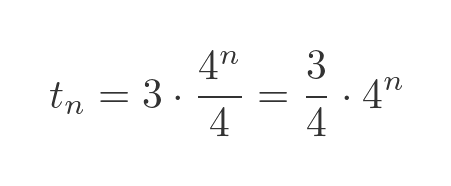
We can also see that the triangles get smaller with each iteration. For each iteration the side length of the triangle is reduced by a factor of 3, so the area is reduced by a factor of 9. If we say that the area of the initial large triangle (iteration 0) is a0, then the area of each triangle at the nth iteration is:

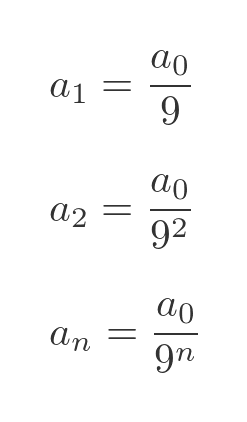
The extra area added by the nth iteration, sn, is the number of triangles times the area of each triangle for that iteration, which is:

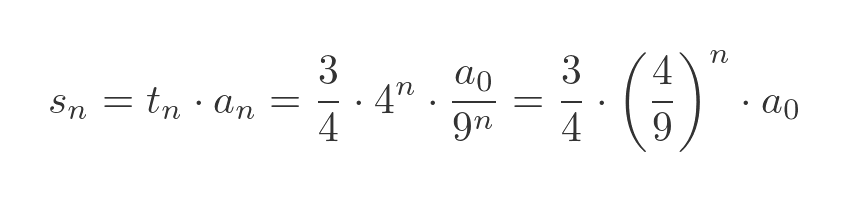
The total area of the snowflake after the nth iteration is equal to the area of the initial triangle plus the sum of all the extra areas up the that iteration:

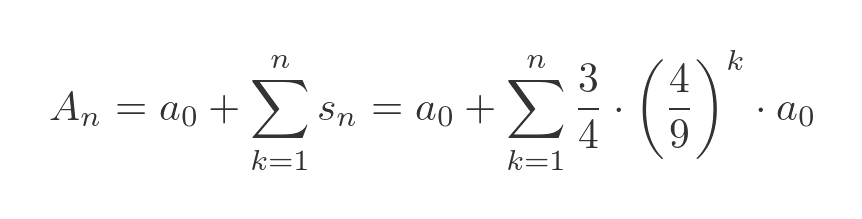
We will take the constant terms out of the sum, and also take out an extra term of 4/9 so that the power inside the sum is k - 1. This will be useful later:

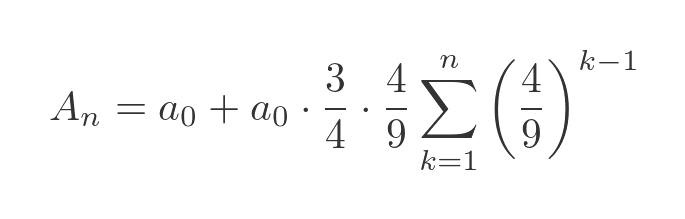
Simplifying:

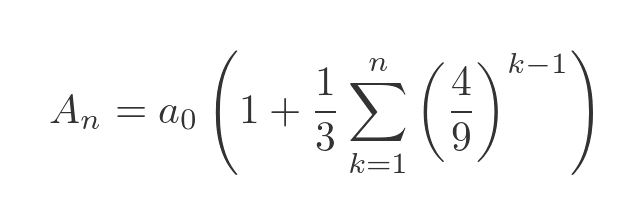
Now we can apply the standard formula for the sum of a geometric series (this is why we converted the power to k - 1):

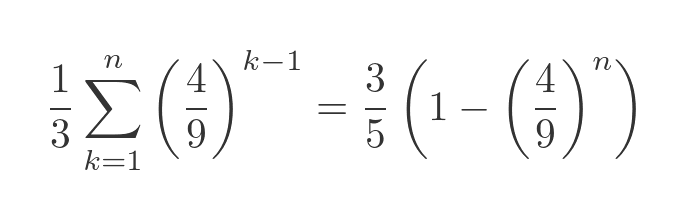
Substituting this into the previous equation and simplifying gives the area of the snowflake after the nth iteration as:

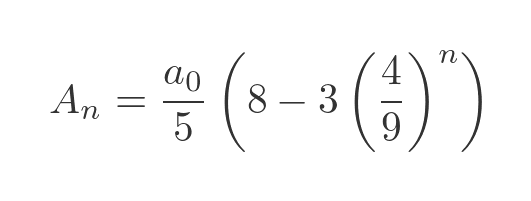
The total area of the final snowflake is the limit of this expression as n tends to infinity. Since 4/9 is less than 1, 4/9 to the power n tends to 0 as n tends to infinity, so the final area is:

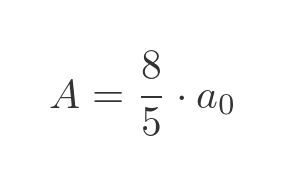
Perimeter of the Koch snowflake

The perimeter is somewhat simpler to calculate.

On each iteration, every side of the snowflake is replaced with 4 new sides. Each of these sides is a third of the length of the side it is replacing. This means that on every iteration, the perimeter of the snowflake increases by a factor of 4/3.

This means that the perimeter increases without bounds as the number of iterations increases. In other words, the perimeter of a Koch snowflake is infinite.

See also

• Bifurcation and chaos
• Cantor set
• Drawing Sierpinski triangles