Cantor set

The Cantor set is one of the simplest fractals, and also one of the earliest to have been studied in detail.

As a one-dimensional structure, it was easy to visualise before modern computers were available.

History of the Cantor set

Georg Cantor is best known for his work on early set theory. One of his most important discoveries, in 1873, was that the set of real numbers is uncountably infinite, which means there is no way to map every real number onto a natural number. This discovery proved that there is more than one kind of infinity - including countably infinite sets (like the natural numbers) and uncountably infinite sets (like the real numbers).

The Cantor set was initially discovered by Henry Smith in 1874. However, it was Georg Cantor who made it famous, introducing it to a wider audience in 1883. The set is interesting because it is made up of two sets of numbers, one countably infinite and the other uncountably infinite.

Creating a Cantor set

Creating a Cantor set is quite straightforward. We start with a line of length 1 unit. This is labelled 1 below:

We then remove the middle third of the line, leaving the two endparts, labelled 2.

To be precise, we remove the open interval between 1/3 and 2/3. This interval does not include the endpoints. This means that 2 sections left behind are closed intervals (i.e. they include the endpoints):

• The range 0 to 1/3.
• The range 2/3 to 1.

We then repeat the process:

What we have done here is to remove the middle third of each of the two remaining sections, again as an open interval. This is labelled 3.

This new line consists of 4 closed intervals, 0 to 1/9, 2/9 to 1/3, 2/3 to 7/9, and 8/9 to 1.

We can repeat this process again and again, each time taking all the previous segments and removing the middle third of each one. The next stages (4, 5 and 6) of this are shown below:

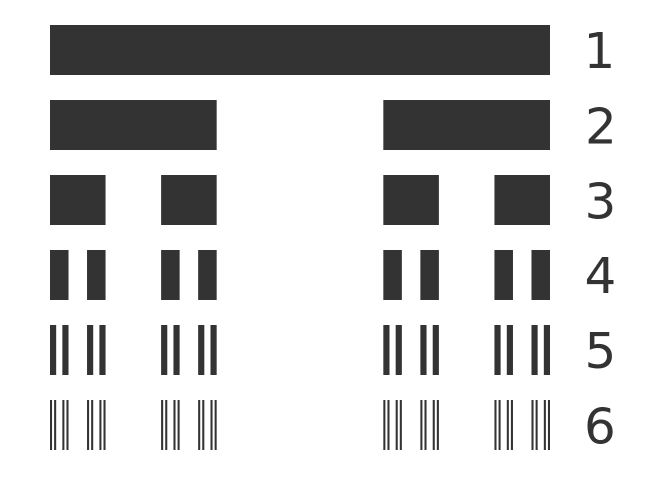
The Cantor is the result if you continue this process forever, for an infinite number of steps.

What is left in the Cantor set

Each iteration in the process above removes a third of the remaining points from the set. This raises the question that, if we keep doing this forever, will there be anything left?

There will be points left, and infinitely many of them, as we will now show.

First, let's consider the points 0 and 1. These are at the outer edges of the original line, marked by the thin red and cyan lines below (the red and cyan dots are only there to make the position of the lines more visible):

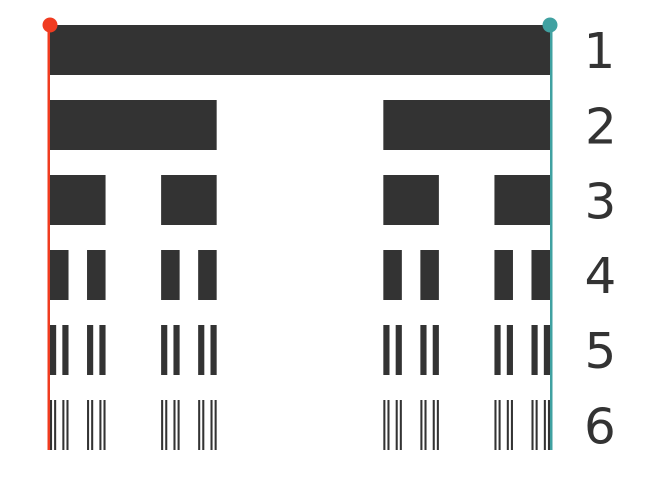
The red line indicates the point 0 in the set. This is part of the initial set because we start with a closed interval [0, 1]. In step 2 we remove the middle third, but this still leaves a closed interval [0, 1/3] on the left, which of course still includes the point 0. In step 3, we remove more points leaving a left-hand edge interval of [0, 1/9], which still contains the point 0.

As we go through more steps, the left-hand interval gets smaller and smaller, but it is always a finite, closed interval, and it always starts at 0. So no matter how many steps we go through, the point 0 will still be part of the Cantor set.

The same logic applies to the point 1. There will always be a rightmost interval that is finite, closed, and ends on 1, so 1 is part of the set.

Next, we will take a look at step 2. In this step, we create 2 new boundaries, at points 1/3 and 2/3. These are shown below, again marked in red and cyan:

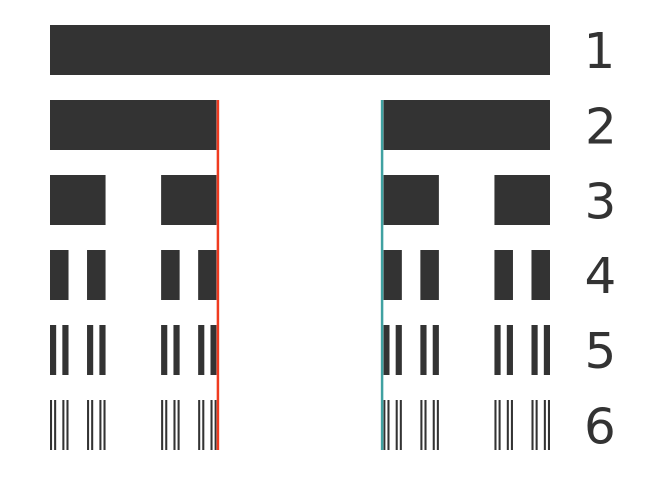
In step 2, there is a closed interval [0, 1/3] that includes the point 1/3. In step 3, the middle of this interval is removed, but it still leaves a closed interval [2/9, 1/3] that includes the point 1/3.

As before, as we go through the steps the interval that ends on 1/3 gets smaller and smaller but it still exists as a finite, closed interval that includes the point 1/3. So the point 1/3 will always remain part of the set. And again, the same logic applies to the point 2/3.

In step 3, we remove more points which creates 4 new boundaries at 1/9, 2/9, 79 and 8/9. These boundary points will never be removed, so they are part of the set. The next step adds another 8 boundary points, then the next step another 16, and so on. This carries on indefinitely so the set contains infinitely many points.

The endpoints form an infinite binary tree - each endpoint at one level creates 2 endpoints at the next level. It can be shown that an infinite binary tree has a countably infinite set of nodes. So, in this case, the endpoints in the Cantor set are countably infinite.

There are other points in the Cantor set

The boundary points aren't the only points in the set. There are other points that form part of the set for a different reason.

One example is the value 1/4, shown here:

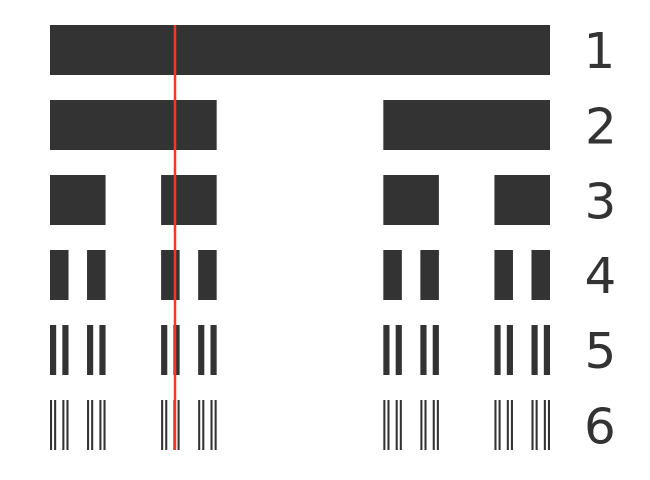
This point isn't eliminated in step 2, because 1/4 is within the range [0, 1/3].

It isn't eliminated in step 3 because 1/4 is within the range [2/9, 1/3].

As we go down the step, the 1/4 line will always pass through one of the black areas so it will not be eliminated. We can go on forever, as the black intervals get smaller and smaller, but the value 1/4 will always be inside one of the black areas no matter how small they get.

This means that 1/4 is part of the set even though it is never on a boundary. This doesn't just apply to 1/4, there are inifinitely many points like that. We will see why later.

Properties of the Cantor set

The Cantor set has some interesting properties.

The first property is that the total length of all the intervals in the set is zero. This means, in effect, that although the set contains infinitely many values, not all of those points join together to form an interval. They are all separate values.

This can be easily proved by adding the total length of the gaps in the set. Looking at the earlier diagram, at step 2 we add a gap of 1/3. In step 3 we add 2 more gaps, each of 1/9. In step 4 we add 4 more gaps, each of 1/27, and so on. The sum of all these gaps is:

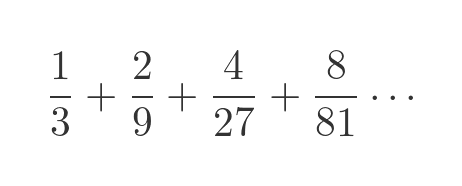
This is a geometric progression, with a ratio of less than 1, so it converges to a value (using the standard geometric progression formula) of:

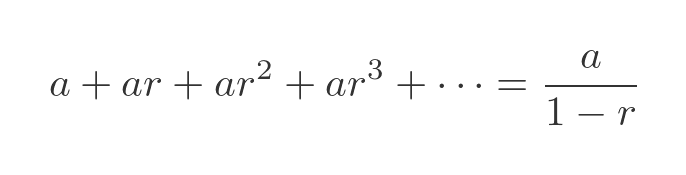
In our case, a is 1/3, r is 2/3, so (r - 1) is 1/3. So the sum of all the gaps is:

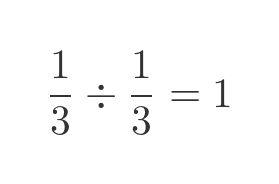
Since the total interval length of the gaps is 1, this means that the total length of the intervals remaining after removing all the gaps is 0.

A second property is that the set contains no isolated points. This means that for any value that is in the set, you will always be able to find another value in the set that is as close as you want to the first value.

These two properties might initially seem contradictory, but they can both be explained by this diagram:

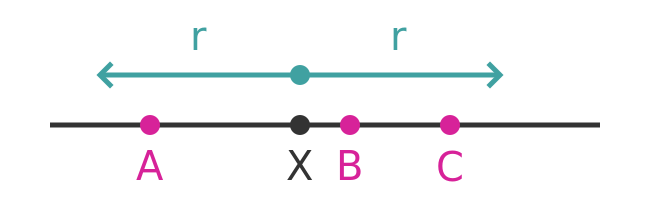
This diagram shows a point X that is part of the set and an interval that is within +/-r of X. There will always be points in the region that are part of the set (such as A, B and C) and there will always be points in the region that are not part of the set. This is true no matter how small you make r (provided r > 0).

A third property is that the Cantor set is uncountably infinite (we will discuss this below). This means it has the same cardinality as the set of real numbers. In other words, the number of elements in the Cantor set is equal to the number of real numbers.

This is quite a strange fact. To create the Cantor set we have removed so many real numbers that the set of numbers left occupies no space on the real number line. But there are still as many numbers left as we started out with!

Why is 1/4 part of the set?

As we have seen, the Cantor set works by dividing the unit interval [0, 1] into 3 parts and removing the centre part. Each remaining range is then divided into 3 parts and has its centre part removed. This is repeated ad infinitum.

Since the set relies heavily on division by 3, we should try to find the most convenient way to represent this, and it turns out that trinary numbers are very useful. More specifically, we will use trinary fractions.

You might wish to read the linked article for more details, but essentially trinary fractions are represented in a similar way to decimal fractions. The difference is that, in trinary fractions, the place values for digits after the point go in powers of 3 rather than powers of 10:

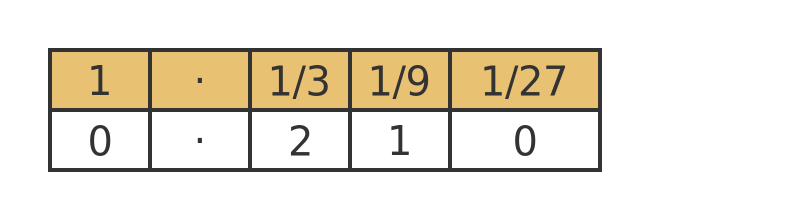
So the value 0.21 in trinary is equal to 7/9.

This is quite useful when we want to describe the points that are in the Cantor set. Let's look at level 2:

To generate the second level, we remove the middle third of the points but leave the rest behind. But remember that in trinary, 0.1 is 1/3 and 0.2 is 2/3. So the two sets that get left behind are the first third, where the numbers take the form 0.0x, and the final third where the numbers take the form 0.2x. The points in the middle, where the numbers take the form 0.1x are eliminated.

There is a minor issue around boundary points, but we will come back to that later.

Now let's look at level 3:

This time we eliminate the middle ninth of the first third. This means we eliminate values of the form 0.01x, and keep values of the form 0.00x and 0.02x. We also eliminate the middle ninth of the last third. This means we eliminate values of the form 0.21x, and keep values of the form 0.20x and 0.22x.

If we go down to deeper levels, we will eliminate any interval where the numbers have a 1 in their trinary fractional form, because that means that at some level they must be in a middle third. The only numbers remaining are those that contain only 0's and 2's in their fractional form.

Now consider the value 1/4. In trinary this is a recurring fraction of the form 0.020202... (as explained in the trinary numbers article linked before). This number contains no 1's, so it will never be eliminated from the set.

The set of all recurring fractions containing only digits 0 or 2 is equivalent to the set of all possible binary sequences (any string of 0's and 1's of any length). It can be shown (using Cantor's diagonal argument) that this set is uncountably infinite and has the same cardinality as the set of real numbers.

Boundary conditions

There is one small problem with the logic above. On each iteration of the Cantor set, we remove the middle third as an open interval, leaving two closed intervals behind. For example, on the first iteration, we remove the open interval 0.1 to 0.2.

A closed interval includes its endpoints. This means that the two closed intervals left behind are (in trinary) 0.0 to 0.1 inclusive, and 0.2 to 1.0 inclusive. And we know that those endpoints will always remain as part of the set.

But 1.0 and 0.1 contain a digit 1. What happened to our rule that every number in the Cantor set must be made only of 0's and 2's?

Well you may recall that, in decimal fractions, 0.999 recurring is equal to 1. The same thing is true of trinary fractions, where 0.222 recurring is equal to 1. This is described in more detail in the trinary numbers article mentioned earlier.

So in base 3, 1.0 can also be written as 0.222..., and 0.1 can be written as 0.0222... In fact, any number that terminates in a 1 can be written using 2's. For example, 0.2021 can be written as 0.20202222... so it is a member of the Cantor set. But 0.2012 can't be written in a way that doesn't contain any 1 digits, so it is not part of the set.

So we can say that any number in the interval [0, 1] is a member of the Cantor set if, and only if, it can be written as a trinary fraction containing no 1 digits.

See also

• Bifurcation and chaos
• Koch snowflake
• Drawing Sierpinski triangles