Solving equations using the Newton-Raphson method

The Newton-Raphson method is a numerical method to solve equations of the form f(x) = 0.

This method requires us to also know the first differential of the function. But the Newton-Raphson method has very good convergence, so it can often provide an accurate result very quickly.

Here is a video on the topic:

Example - square root of two using Newton-Raphson method

As a simple example, we will solve the equation:

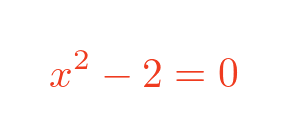
This equation has a solution x = √2 (and an second solution x = -√2). We will only look for the first solution. Although we already know the answer to the problem, it is still useful to work through the numerical solution to see how it works (and to gain an approximate value for the square root of 2).

To use the technique we need to have a rough idea of where the solution is. It is useful to sketch a graph of the function:

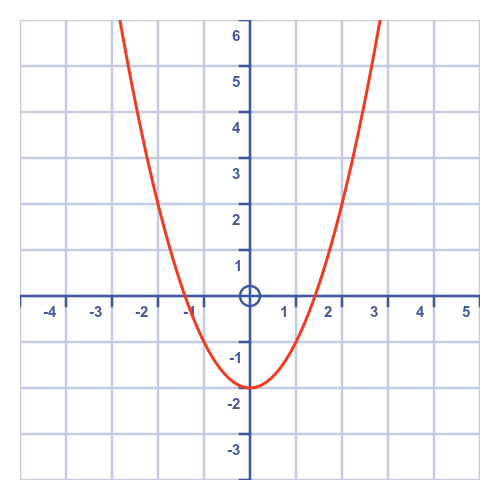
The Newton-Raphson method starts with an initial guess at the solution. The guess doesn't need to be particularly accurate, we can just use the value 2.

The Newton-Raphson method proceeds as follows:

1. Start with an initial guess x (2 in this case).
2. Draw a tangent to the curve at the point x.
3. Find the value of x where the tangent crosses the x-axis. This will be the next value for x.
4. Repeat from step two with the new value.

Steps 2 to 4 are repeated until a sufficiently accurate result is obtained, as described in the solving equations article. On each pass, the new guess is usually closer to the required result, so the approximation becomes more accurate. When the result is accurate enough, the process ends.

A graphical explanation of the Newton Raphson method

To gain an intuitive understanding of the process, we will go through a couple of iterations and show the results on a graph. This is for illustration only, you don't need to draw an accurate graph to use this method. Once we understand the method it can be calculated without requiring a graph.

First iteration

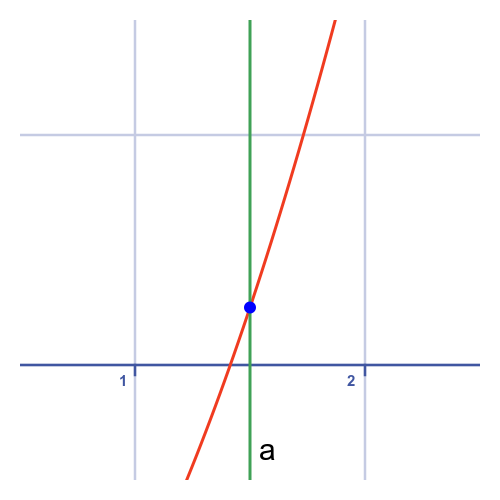
The first iteration starts with a guess of 2. Here is the graph where we have zoomed in on the region of interest. a shows the line x = 2:

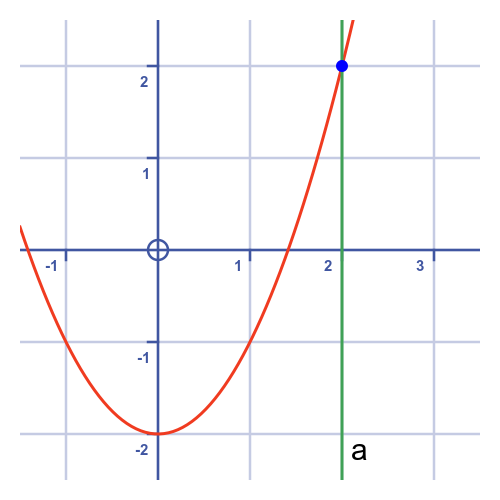
We now draw a line that forms a tangent to the curve at x = 2:

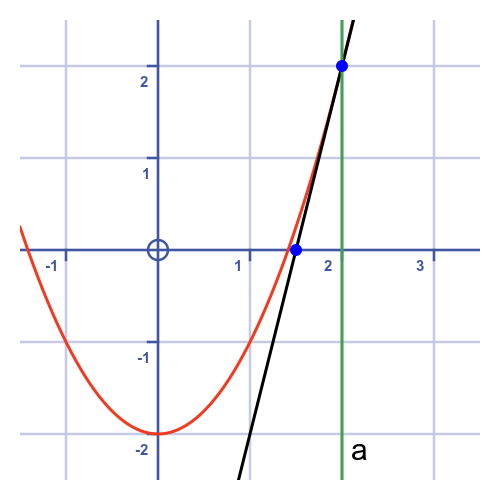
This tangent line hits the x-axis at x = 1.5. This forms our second approximation.

The formula for calculating the next value of x is shown later in this article.

Second iteration

The second iteration starts with the new value of 1.5. On the graph below, we have zoomed in on the range 0.5 to 2.5:

Again, we draw a tangent. Notice that at this stage the curve itself is very close to being a straight line, so the tangent is very close to the curve when it hits the x-axis.

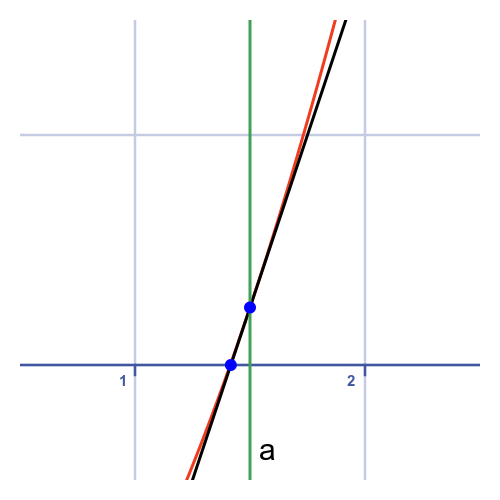
The tangent hits the x-axis at 0.4666...

Deriving the formula

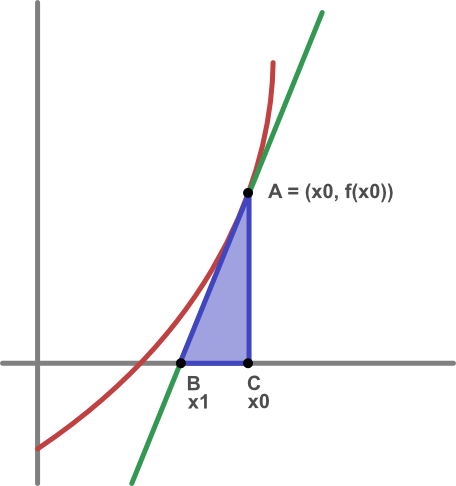
This diagram shows a curve y = f(x) with its tangent at point A. We need to calculate the position of point B, where the tangent crosses the x-axis.

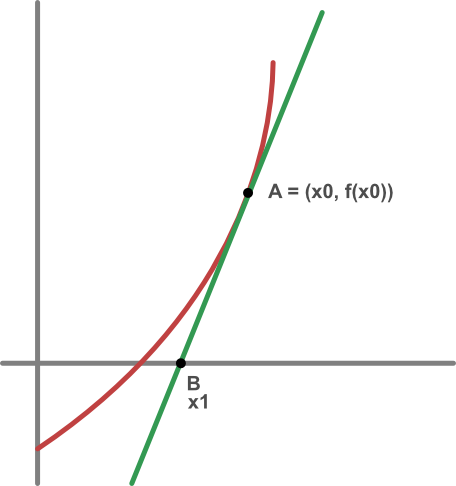
If point A has an x-value of x₀, then its y-value will be f(x₀) because the point is on the curve.

Since the line AB is a tangent to the curve, we also know that the slope is equal to the slope of the function curve at point A, which is the first derivative of the curve at that point:

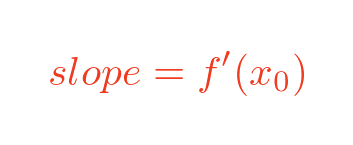
Next we can draw a right-angled triangle ABC where C is on the x-axis directly below A (ie at point x₀):

This triangle tells us that the slope of the line AB is:

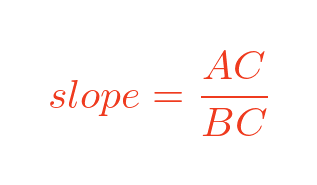
Since the length of AC is $f(x_0)$ and the length of BC is x₁ - x₀, we have

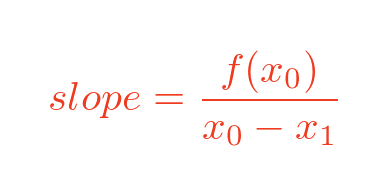
We now have two separate expressions for the slope of the line AB, so we can equate them:

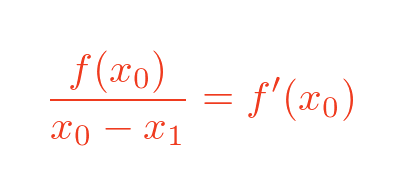
Inverting both sides gives:

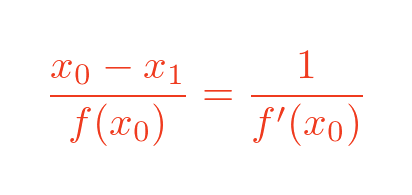
So:

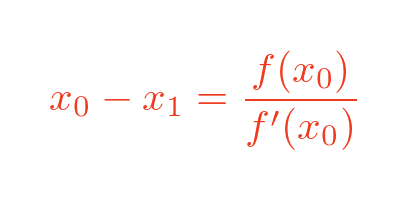
Rearranging the terms gives the final result for x₁:

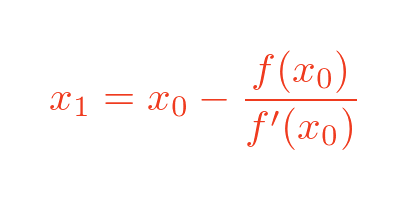
This is the general formula for solving f(x). The particular formula we are solving in this example is:

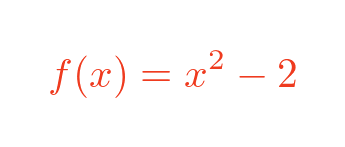
Which has a first derivative:

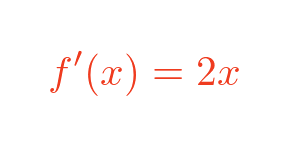
So our equation is

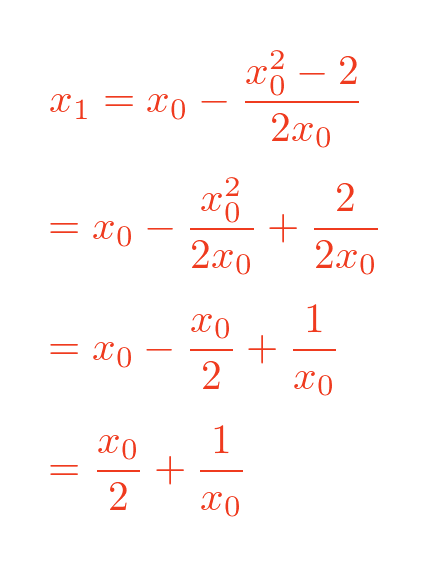
Newton-Raphson method by calculation

The method for finding the root is very simple:

1. Start with the initial guess for x.
2. Use the formula to calculate the next value of x.
3. Repeat step two with the new value.

Steps 2 to 3 are repeated until a sufficiently accurate result is obtained, as described in the solving equations article. On each pass, the value of x should typically get closer to the root.

In this case, the formula is:

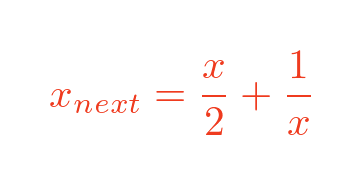
Starting with x = 2, applying this equation gives:

• 1.5
• 1.4666...
• 1.4142156862745097
• 1.4142135623746899
• 1.414213562373095

After 5 iterations, the result is correct to about 15 decimal places!

Advantages and disadvantages of the method

The main advantage of the Newton-Raphson method is that it often converges very quickly.

There are several disadvantages. The first is that some analysis is required for each formula. For example, it took a few lines of calculation to discover the formula for finding the square root of 2. If we wanted to find the cube root of 2 we would need to do a similar, but slightly different, calculation.

Another disadvantage occurs in some cases where there is more than one root. Depending on the initial value of x the method will often converge on the nearest solution. But that isn't always true. In some situations, the method will end up converging on a different root that is further away from the starting value. It isn't always easy to predict which root the method will converge on from a given starting point.

In some cases, attempting to map the start value onto the final root can result in a highly complex, fractal-like pattern, called a Newton Fractal. Unfortunately, poor old Joseph Raphson doesn't get credited with this fractal, even though neither he nor Newton discovered it.

Finally, it is sometimes possible for the formula to never converge on a root. This can usually be corrected by choosing a different initial value.

This makes the method very useful for calculating common values such as square roots, or other roots. The analysis only needs to be performed once, it is possible to devise starting conditions that are known to always work, and the calculation converges very quickly.

Newton-Raphson method calculator in Python code

As an illustration, we will create a simple Python routine that acts as a Newton-Raphson calculator for the square root of any positive value.

For square roots, calculating the square root of 2 every time isn't very useful. We would like to calculate the square root of any positive value a. This requires a slight modification to the formula:

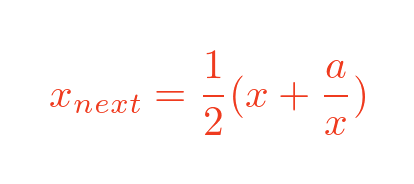
Here is the Python code to calculate this:

def square_root(a):
    x = a

    while True:
        x_next = (x + a/x) / 2
        if abs(x_next - x) < 0.0000001:
            break
        x = x_next

    return x

print(root(2))
print(root(9))
print(root(10))

Within the square_root function, we loop calculating the next x value using the formula.

We need to decide how many times to do this. There are various ways to do this, but in this code we simply check the absolute difference between the old value of x and the new value of x. Because the x² function is a simple U-shape, the approximation always gets better on every iteration of the loop. So when x reaches the point that it is hardly changing between iterations, we know that the value is reasonably accurate. In this case, we stop when the value is known to about 6 decimal places.

See also

• Solving equations numerically
• Solving equations using interval bisection
• Solving equations using linear interpolation
• Numerical integration