The seven bridges of Königsberg

The problem of the seven bridges of Königsberg was a popular problem in mathematics in the early 1700s. It was solved by Euler in 1736, and although the problem itself wasn't especially difficult, Euler's solution laid some of the groundwork for modern graph theory.

The problem

The city of Königsberg was split by the Pregal River, which ran through the middle of it. The city occupied both banks of the river, as well as two large islands in the river, so Königsberg was divided into 4 land masses, like this:

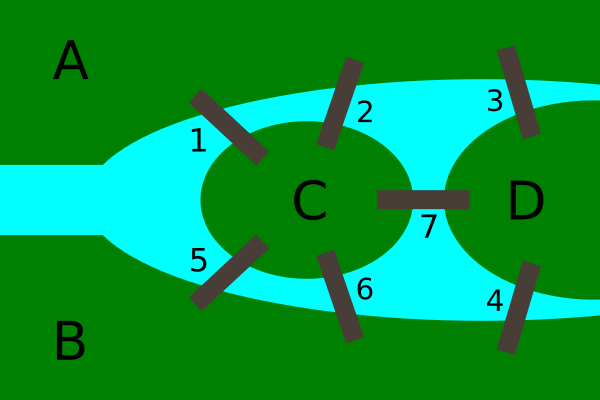
The parts are labelled A to D on the map. The parts are joined by 7 bridges, and shown. They are labelled 1 to 7.

The problem can be simply stated as: is it possible to walk around the city crossing every bridge exactly once?

To avoid obvious cheats you are not allowed to cross the river in any way except via a bridge. You are not allowed to use a boat, or swim, or anything else like that.

Also, crossing a bridge means getting on at one end, walking across, getting off at the other end, and then never using the bridge again. You are not allowed to walk along the bridge and back again (which would mean you had "crossed" the bridge but were back where you started).

Significance

This might not seem like a groundbreaking mathematical problem. It is something that these days we might call a brainteaser and ask a child to try to solve by trial and error.

Euler, of course, analysed the problem in more depth to develop a mathematical proof of whether or not the walk was possible. In doing this, he had to develop ideas that now form part of graph theory, and in fact his solution is regarded as the first theorem of graph theory.

The seven bridges as a graph

The first this Euler did was to remove all the unnecessary details. For example, it didn't matter how you travelled from one bridge to another. All that mattered was which bridges you crossed, in which order, and in which direction.

Each land mass could therefore be represented as a point, and each bridge could be represented as a connection between 2 of those points. This type of diagram is what we now call a graph diagram.

Here is a graph representing the bridges. We have labelled each vertex (or node) with a letter corresponding to the land mass it represents, and each edge (or connection) with the number of the bridge it represents:

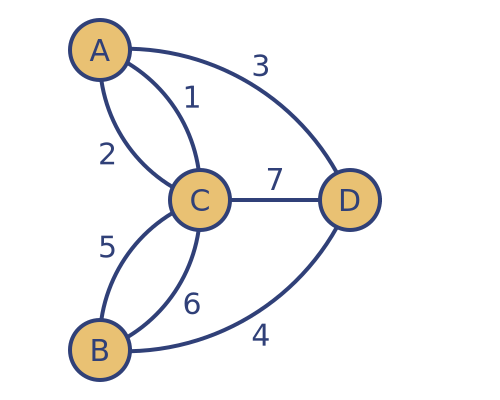
In modern terminology, we call this an undirected multigraph. It is undirected because you are allowed to traverse any edge (i.e. cross any bridge) in either direction. It is a multigraph because there can be multiple edges (or bridges) between the same 2 vertices. For example A and C are joined by two edges, numbered 1 and 2.

Euler's proof

Euler proved that it is indeed not possible to walk around the city using every bridge exactly once. His reasoning was as follows.

There are 2 possible ways you might walk around the city. You might start at one vertex (we will call it the S vertex), and end at a different vertex (we will call it the E vertex). Clearly in order to use every edge you must visit every vertex, so the other two vertices will be intermediate vertices (neither a startpoint nor an endpoint), which we will call I vertices.

Alternatively, you might start and end at the same vertex (we will call it the SE vertex). You must still visit all the other three vertices, which again we will call I vertices.

If there is a route around the city that uses every bridge exactly once, it must follow one or the other of those 2 patterns.

Now consider an I vertex (that is, neither a startpoint nor an endpoint). Every time we enter that vertex, we must also leave that vertex (since we don't start or end there). So the sum of the number of times we enter and leave must be an even number. Each time we enter or leave it must be by a different edge. So, in order to use each edge exactly once, an I vertex must have an even number of edges.

Since there are at least 2 I vertices, this means that there must be at least 2 vertices that have an even number of edges.

But in this case, A, B and D each have 3 edges (in modern graph theory we say these vertices have a degree of 3). vertex C has a degree of 5.

Since no vertices have an even degree, it is not possible to walk around the city using every bridge exactly once.

Making the route possible

We could make the route possible by removing a single edge. For example, if we removed the edge between C and D that would mean that those 2 vertices would both have an even degree:

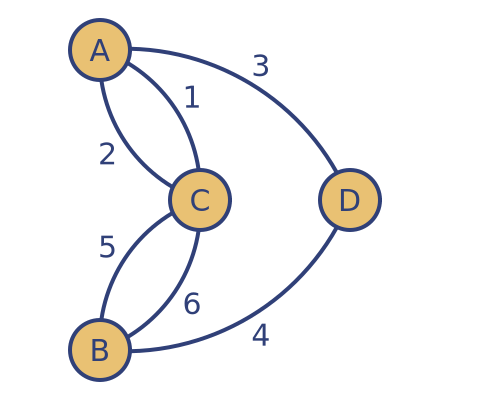
We must start at A or B because those vertices have odd degrees. One route would be to start at A and follow the edges in the order they are numbered, ending on B.

We could also make it possible by adding a single edge, for example between A and B:

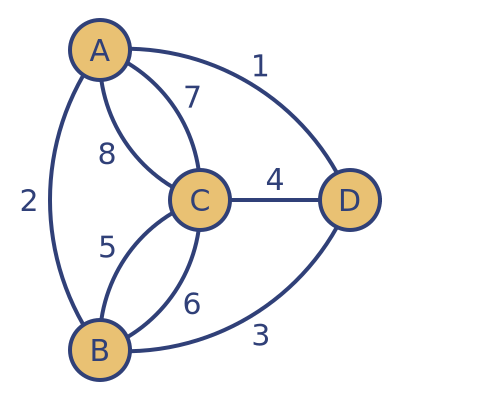
This time we must start at C or D because those vertices have odd degrees. One route would be to start at D and follow the edges in the order they are numbered, ending on C.

Euler trails and tours

In graph terminology:

• A walk is any sequence of edges in a graph (see the graphs article). A walk can visit a vertex more than once, and use an edge more than once.
• A trail is a special type of walk that doesn't use any edge more than once.
• A tour is a trail that starts and ends on the same vertex.
• A path is a special type of walk that doesn't visit any vertex more than once, and doesn't use any edge more than once.

A trail that visits every single edge in the graph exactly once is called an Eulerian trail. The two previous examples were Eulerian trails, but the original Königsberg layout isn't, because it isn't possible to visit all the vertices without repeating an edge.

An Eulerian trail is sometimes called an Euler walk or an Eulerian path . Notice, though, that it is not strictly a path according to modern graph terminology, because it might visit the same vertex more than once.

An Eulerian tour is a tour that visits every edge exactly once. This is sometimes called an Eulerian circuit.

See also

• Graphs
• Adjacency matrices
• Permutation matrices and graphs
• Dijkstra's algorithm
• Travelling salesman problem