Finding the speed of light

We now know that light travels at approximately 300,000,000 metres per second. Measuring something that travels so fast is a difficult task, and has occupied some of the best scientific minds for several centuries.

The further discovery that light always travels at the same speed, regardless of the frame of reference, led to the development of Einstein's theory of special relativity, which gave us a new and deeper understanding of how the universe works.

In this article, we will look at some of the most important experiments from the scientific quest to measure the speed of light.

Ancient ideas about light

In ancient times, the nature of light was not well understood. Some of the earliest documented ideas about come from ancient Greece.

In those days, there were relatively few sources of light. The Sun was the main source of light, of course. The Moon was generally thought of as a source of light, although some ancient Greek philosophers were aware that the Moon only reflected light from the Sun, and recognised that as the cause of the phases of the Moon. The stars were also a source of light, although barely enough to see by on a moonless night. The other occasional source of light was lightning.

They also knew about fire, of course, and used it for artificial lighting. They had oil lamps, candles, and torches (powered by flame, not batteries!).

The idea of light travelling from a source, bouncing off an object, and entering the eye was not fully established. There were three main ideas:

• Empedocles is associated with the earliest known theory, which is also the one most similar to modern theories. He suggested that light was something that moved through space. And, like anything that moves, he reasoned, must have a finite speed.
• Aristotle believed that light was the "actualisation" of a transparent medium (such as air or water) in response to the colours of objects. In that sense, light didn't travel, it just existed in space. So the concept of the speed of light had no meaning.
• A later theory by Euclid and others, the emission theory of vision, suggested that light was emitted from the eyes to enable vision, perhaps in a similar way to modern radar systems. Light, in that theory, was invisible, so not the same thing as the light from the Sun. Heron of Alexandria went on to suggest that this must mean that light has infinite speed, because when you open your eyes, even the most distant objects immediately become visible.

Advances in the 17th and 18th centuries

By the 17th Century, the general consensus was that light travelled through space, and it was clear that it travelled quite quickly, but nobody knew whether the speed was infinite or just very fast.

Galileo and others attempted to measure the speed of light directly, using a simple experiment. Two people, A and B, would stand some distance apart, each holding a covered lantern. The experiment was performed on two hilltops, about a mile apart. This is represented on this diagram:

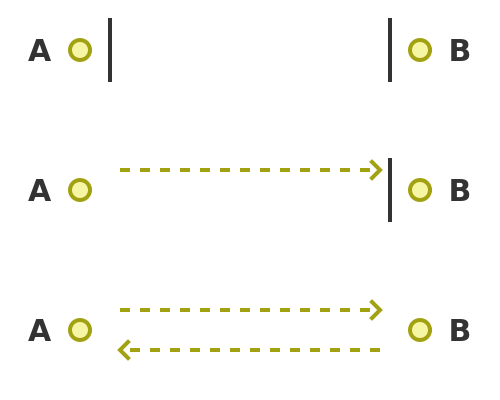
The top part shows the initial condition, with both lanterns covered.

Next, person A would uncover their lantern. The light would travel A to B. This is shown in the middle part of the diagram.

On seeing the light from lantern A, person B would uncover their lantern. The light would then travel B to A. This is shown in the bottom part of the diagram.

The aim of the experiment was that person A would uncover their lantern, and then a short time later they would see the light from lantern B. The time delay would be the time it took for light to travel 2 miles (one mile in each direction), and the speed of light could be calculated from that.

Of course, Galileo was aware that each person would take a short time to see the light and react to it. This could be accounted for by experimenting with the lanterns much closer together, so the measured time would be mainly dependent on the reaction times.

Galileo found that the time taken for the light to travel 2 miles was so short that it was insignificant compared to the reaction times. So he concluded, quite correctly, that the speed of light was either infinite or so fast that it couldn't be measured by the experiment. We now know that the time light takes to travel 2 miles (roughly 3,000 m) is 10 microseconds, which is far too short to be measured by the experiment.

Observing planets

It was clear that 2 miles was far too short a distance to be able to measure the time taken using any techniques available at the time. It was necessary to find a way to observe light travelling far greater distances. Science was making great advances in astronomy at the time. One particular object of interest was one of Jupiter's moons, Io. Galileo discovered this moon in 1610. It orbits Jupiter in slightly less than two days (actually 1.769 days), and it passes behind Jupiter on each orbit.

Why the interest in Io? Well, at the time, there was an ongoing problem with ship navigation. To determine the longitudinal position of the ship (that is, how far around the globe the ship is in the East/West directions, it was necessary to know two things:

• The Ship's local time of day. This could be found from the position of the Sun in the sky.
• The time at some fixed place, for example, Greenwich in London. This required a clock that could keep accurate time for the entire journey of weeks or months.

Unfortunately, in the 1600s, there were no accurate clocks. Certainly, none that could keep accurate time for weeks or months. But Galileo reasoned that the moon Io could be seen from anywhere in the world, and because its motion was predictable, it could be used as a worldwide clock. It was to calculate tables that showed the exact time (in London or wherever) that Io disappeared behind Jupiter. Navigators could then calculate their longitude, once every couple of days. On a journey of several months, that is far better than having no idea at all.

In the 1670s, Danish astronomer Ole Rømer spent several years observing Io, noting the exact times Io disappeared behind Jupiter. He was doing this to gather data for navigation purposes. But he noticed something very strange. Although the eclipses happened every 1.769 days as expected, at some times of the year, the eclipses happened slightly earlier than expected, and at some times slightly later.

Here is a diagram of what is going on (not to scale, of course):

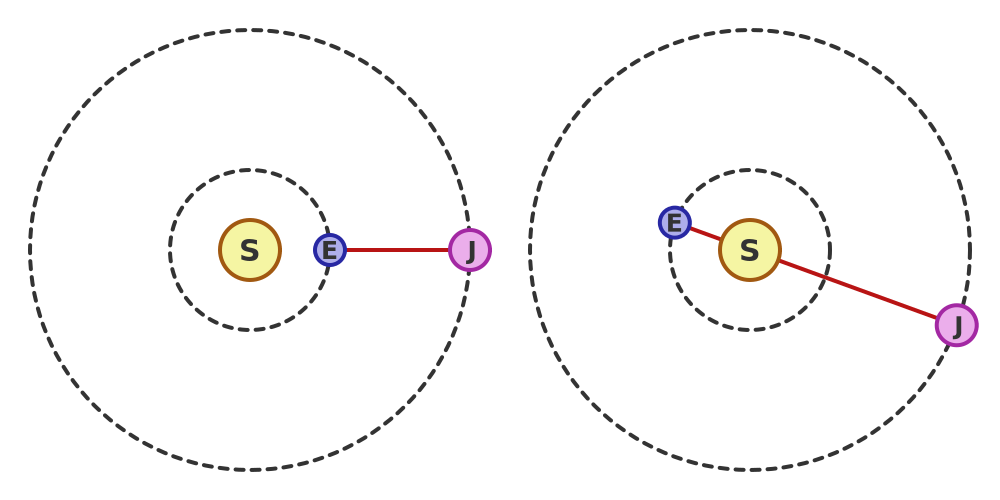
The LHS shows the situation when the Earth is on the same side of the Sun as Jupiter. The distance between the two planets is at its minimum.

The RHS shows the situation a little over 6 months later. Jupiter takes about 12 years to orbit the Sun, so it will only have moved through a small angle. The Earth is on the opposite side of the Sun, and is as far from Jupiter as it can be.

An observer on the Sun would see the moon Io disappear behind Jupiter once every 1.769 days, like clockwork. An observer on Earth in the LHS situation would also see Io disappear behind Jupiter once every 1.769 days (there would be a tiny difference due to the orbital movement of the Earth, but we can ignore that). But because the Earth is closer to Jupiter, the observer would see the event earlier than the observer on the Sun. The time difference would be the time taken for light to travel between the Earth and the Sun, which we now know is 8 minutes 20 seconds.

In the RHS situation, Earth is further away from Jupiter, so light would take longer to get here by the same amount of time. Over the course of approximately a year, the timings would move between the two extremes. This diagram illustrates the principle, based on 10 readings over that time (the variation is exaggerated for clarity):

The top, orange lines show the time Io disappears behind Jupiter, according to an observer on the Sunn.

The bottom, blue lines show the same events as observed on Earth. As expected, the events are sometimes observed earlier or later, based on the time of year. By analysing these times, it is possible to calculate the speed of light. The maximum difference in times is equal to the time taken for light to travel twice the distance from the Sun to the Earth.

At the time the experiment was performed, it was only possible to measure the times with limited accuracy, and the radius of the Earth's orbit was not known accurately either. Christiaan Huygens first calculated the speed of light using Rømer's data, and came up with a result of approximately 210,000,000 m/s. This is certainly in the same ballpark as the true value (around 300,000,000).

Measuring the speed of light in a lab

Armed with a rough idea of the speed of light and some technical innovation (including good quality mirrors, and steam-powered high-speed rotation), in the 19th century, it became possible to measure the speed of light directly on Earth. Several methods were tried, but the first really successful experiment was performed by Léon Foucault in 1850. His setup was something like this:

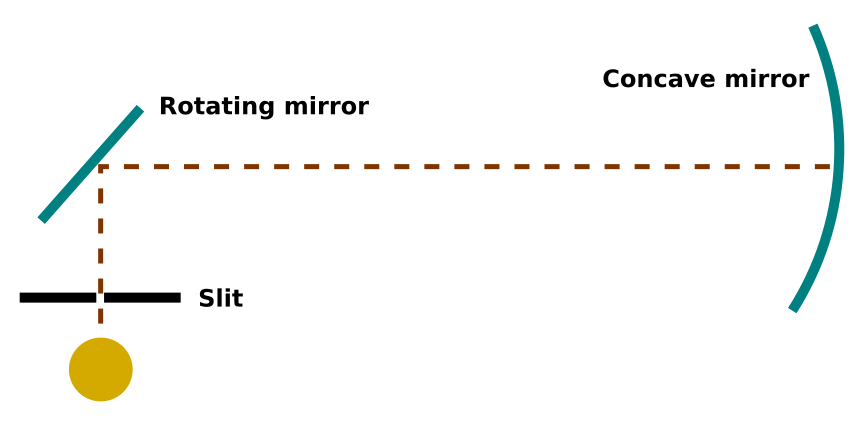
First, consider the situation when the rotating mirror is held in a fixed position. Light from the source passes through the slit, reflects off the angled mirror, and hits the concave mirror. It then reflects back to the angled mirror and back to the slit. The concave mirror is designed to have curvature such that the beam always goes back through the slit, even if the angled mirror is changed to a different angle.

Now consider what happens when the angled mirror rotates rapidly. The light initially takes the same path, through the slit, to the angled mirror, to the concave mirror, then back to the angled mirror. But since the angled mirror is rotating rapidly, by the time the light strikes it for a second time, it has changed angle very slightly. This means that the reflected beam doesn't go back into the slit. Instead, it forms an image next to the slit. The position of the image, together with the speed of rotation and the distance the light travels, can be used to calculate the speed of light.

Foucault's measurement was within 0.6% of the modern known value.

Maxwell's equations

Despite being able to measure the speed of light very accurately, nobody really knew what light actually was. But entirely separate work had been going on to study electricity and magnetism, resulting in Maxwell's equations in 1865.

One outcome of the equations was the ability to calculate the "speed" of electricity and magnetism - that is, how quickly a change to an electromagnetic field would propagate through space. This could be found in terms of two constants, the permittivity of free space (ε₀) and permeability of free space (μ₀). These values were measured experimentally, and gave a resulting speed that was remarkably close to the measured speed of light. This gave a strong hint that light might in fact be an electromagnetic wave.

The equations also foreshadowed relativity. First, they indicated that (at least for electromagnetic forces) there could be no instantaneous action at a distance. The effects of a change happening in one location can only reach a distant location at the speed of light.

More subtly, and not fully understood at the time, Maxwell's equations implied that the speed of light is the same in any frame of reference. This became the key problem that relativity would address.

There was still a belief that, if light is a wave, it surely must have a medium - a wave has to travel through something. As ocean waves travel through water, and sound waves travel through air, then light waves must travel through something physical. At the time, Maxwell and others imagined an aether must exist. There were two possibilities: either that aether was present in space and the Earth moved through it (the aether wind theory), or the aether close to the Earth was dragged round with the Earth, as happens with the oceans and atmosphere.

The famous Michelson–Morley experiment attempted to detect differences in the speed of light in two perpendicular directions. The method was broadly similar to earlier experiments, such as Foucault's experiment. The main difference was that it used a half-silvered mirror to split the light beam and send it in two different directions. It used interference between two returning beams, which was capable of detecting small differences in speed between the two directions.

The result of the experiment was negative, eliminating the aether wind theory, which some regarded as the most likely behaviour of the aether. This was another piece of evidence that fed into the theory of relativity in the early 20th century.

Resonance methods

Louis Essen and A. C. Gordon-Smith measured the speed of light even more accurately in a 1950 experiment. By the time, of course, radio waves were well understood and known to be another form of electromagnetic radiation. A lot of work had also been done on microwaves, in part to develop effective radar during WWII. It was also known that the wavelength, frequency, and speed of a wave are related by the formula:

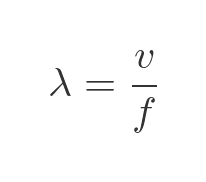
Here λ is the wavelength of the microwave, f is its frequency, and v is the speed (the speed of light). The Essen–Gordon-Smith experiment used microwaves of a known frequency and used a resonance chamber to measure the wavelength very accurately.

With accurate values for f and λ, the speed of light could be found. They determined the speed of light to be 299792500 +/- 300 m/s.

Laser interferometry

With the development of lasers, it became possible to produce a highly coherent beam of light with a single frequency (ie monochromatic light). This allows the wavelength to be measured very accurately using interference. In 1972, K M Essen and others measured the speed of light to be 299,792,456.2 +/- 1.1 m/s.

The definition of the speed of light

At this stage, measuring the speed of light was primarily limited by our ability to measure distance. Or, put another way, the most precise way to measure distance is laser interferometry.

In 1983, the General Conference on Weights and Measures took the step of defining the speed of light to be exactly 299,792,458 m/s.

This means that the metre is now defined to be the distance light travels in 1/299,792,458 of a second. This also means that, if we continue to find better ways to measure the speed of light, the value of the speed of light won't change, we will just have a more precise idea of what a metre is!