Sleeping Beauty problem

The Sleeping Beauty problem was created in the 1980s. Although it appears to be a fairly simple probability problem, it remains controversial, with no solution being generally accepted.

The problem

The problem is expressed as an experiment which Sleeping Beauty has agreed to take part in.

On Sunday she will be given a sleeping drug. Then a fair coin will be tossed, which affects what happens in the rest of the experiment.

During the experiment, she will be woken up either once (on Monday) or twice (on Monday and Tuesday), depending on the coin. If the coin comes up heads she will only be woken up once, if it is tails she will be woken up twice. Each time she is woken up she will be interviewed and then put back to sleep. Finally, on Wednesday, she will be woken up again and the experiment will be over.

Crucially, the sleeping drug has an amnesiac effect, so each time she is woken up, she will have no memory of being woken up before. She won't know if it is Monday, Tuesday or Wednesday, and will have no recollection of what was said in any previous interviews. She won't even know if any interviews have already taken place.

Each time she is interviewed, she is asked for her level of credence that the coin had come up heads (that is, her estimate of the probability that the coin had come up heads).

She has been told all the details of how the experiment works, but she does not know the result of the coin toss and has no way of knowing if it is Monday or Tuesday when she is woken and interviewed. What should she answer?

There are three main positions on this question.

The halfer position

The so-called halfer position states that Sleeping Beauty should say she is 50% certain the coin came up heads. The reasoning is that when the coin was tossed, the probability of the coin being heads was 1/2.

The coin toss had already happened before she was first awakened, so nothing about her awakening could possibly affect the outcome. Indeed, nothing at all could affect the outcome after it has happened.

In addition, her awakening provided her with no new information. She wasn't told the result of the toss, and she had no way of knowing how many times she had been awakened.

With an event that had already happened, and having received no new information, how could the probability of heads possibly be anything other than 1/2?

The thirder position

An alternative position, called the thirder position, argues that her credence that the coin came up heads should be 1/3.

Each time she is awakened and interviewed, she must be in one of the following three circumstances:

1. It is Monday, and the coin came up heads.
2. It is Monday, and the coin came up tails.
3. It is Tuesday, and the coin came up tails.

There are no other possible situations. The experiment doesn't allow for her to be awakened and interviewed on any day other than Monday or Tuesday, the coin has to be either heads or tails, and she won't be woken on Tuesday if the coin comes up heads, so the three options above are the only possibilities. And, of course, only one of those conditions can be true at any time (it can't be Monday and Tuesday, and the coin can't be heads and tails).

Let's assign probabilities of each of these cases, as P(Day, coin). The probabilities of the three situations above are P(M, h), P(M, t), and P(T, t). Since these three possibilities are exhaustive (no other situation can exist) and exclusive (no more than one can be true), then the three probabilities must add to 1:

Now let's imagine that Sleeping Beauty was awakened and somehow discovered it was Monday. Perhaps the interviewer had accidentally left his computer screen visible, showing the date. Knowing it is Monday, there are only two possibilities - it is Monday and the coin was heads, or it is Monday and the coin was tails. Since heads or tails are equally probable, then these two possibilities are equally likely:

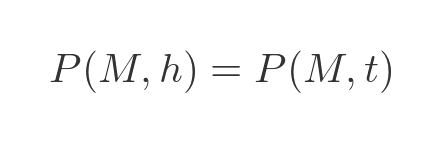
Although we have assumed that Sleeping Beauty knew it was Monday, whether she knew that or not can't affect the probability of the coin being heads or tails, so the equation above is generally true, even if she didn't know the day

Alternatively, let's imagine that Sleeping Beauty somehow discovered that the coin came up tails. Knowing this, there are again only two possibilities - it is Monday and the coin was tails, or it is Tuesday and the coin was tails. Since Monday or Tuesday are indistinguishable to her, then these two possibilities are equally likely:

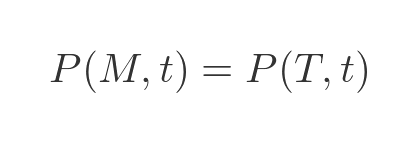
Both equations include P(M, t), so all three probabilities are equal. And since we know the three probabilities add up to 1, each must be equal to a third:

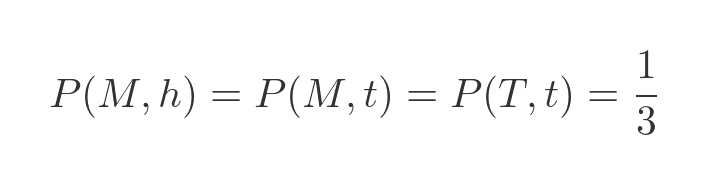
Ambiguous question position

An attempt to resolve these two positions is to say that the question itself is ambiguous, and depending on the interpretation of the question the probability might be 1/2 or 1/3.

The ambiguity arises from two alternative ways of interpreting the question.

We could interpret the question to mean: what is your credence that, when the coin was tossed, it came up heads? Now clearly, when the coin was tossed, the chance that it was heads would be 1/2. So the answer to this question must be 1/2. If the coin happened to come up tails, Sleeping Beauty would get asked the question twice, but her answer on both occasions would have to be 1/2.

Alternatively, we could take it to mean: what is your credence that the coin toss that led to this awakening was heads? Now in this case she might be in one of three situations - (M, h), (M. t) or (T, t). If we accept that these situations are equally likely, then here credence would be 1/3.

To understand this distinction, imagine a different experiment. We toss a coin many times. Each time, if the coin comes up heads we write "heads" on a card and put the card into a box. If the coin comes up tails we write "tails" on two cards and put both cards into the box.

After doing this many times, if we ask what was the probability of adding a heads card to the box after each coin toss, then of course it is 1/2. But if we drew a card from the box at random, the probability of drawing a heads card would be 1/3, because there are twice as many tails cards as heads cards in the box.

Adding a heads card to the box, of course, is analogous to the coin coming up heads in the experiment. Drawing a card from the box is analogous to Sleeping Beauty trying to guess if the coin came up heads. She will be right more often if she guesses tails because she will get an extra guess if the coin did, in fact, come up tails.

The disparity arises, in part, because Sleeping Beauty is in quite an unusual position of having no knowledge of a decision she made the day before. If she could remember the previous awakening, of course, it would be far easier. On Monday, she would be 50% certain the coin was heads. On Tuesday, if she was asked, she would know for certain it wasn't heads.

What do you think?

Please let me know what you think (and why!) in the comments.

My own opinion? Given that this problem has been around since the mid-1908s, so it is 40 years old, and people are still undecided, I find myself drawn to the ambiguous question solution.

Certainly, if the question is interpreted as what is your credence that, when the coin was tossed, it came up heads?, then the answer is 1/2.

However, to support the ambiguous question still requires two more assumptions:

• First, is it reasonable to interpret the question in two different ways? Some might feel that the question can't be interpreted as referring to the original coin toss. After all, why bother putting the subject to sleep in order to ask them a trivial question about tossing a coin? Or maybe that is the point.
• It also assumes that the logic of the thirder position is sound.

Yet, I still feel there is something fishy about the thirder position. Not that the statistics aren't correct - clearly if you conducted the experiment many times then heads would only be the correct answer in a third of all the interviews conducted.

But the reason for that is simply that the experiment is designed so that, if the coin comes up tails, the question is asked twice. The same question, with the same answer. And, since Sleeping Beauty doesn't know what day it is, there is a high probability she would always give the same answer. It would be difficult for her to even give a random answer each time, not knowing what or even if she had answered previously.

This feels suspiciously like double counting.

Consider this alternative experiment. Someone tosses a coin and Sleeping Beauty has to guess if it is heads or tails. If she calls heads and she is right, she wins £100. If she calls tails and she is right, she wins £200. If she guesses wrong she wins nothing.

Now clearly she should call tails because she is just as likely to be right as if she called heads, but she stands to win twice as much. But if she were asked to state her credence that the coin was heads, then in this situation she would have to say 1/2. The fact that she stands to win twice as much money doesn't make that outcome more likely, although she might be tempted to pretend it does.

What do you think?

See also

• Monty Hall problem
• Pigeonhole principle
• Drunk man and keys problem
• Raven paradox
• Painter's paradox
• Potato paradox
• Russell's paradox
• Surprise exam paradox
• Coin rotation paradox