Painter's paradox

The painter's paradox is a paradox relating to an interesting 3D shape called Gabriel's horn.

Gabriel's horn

Gabriel's horn is based on the function:

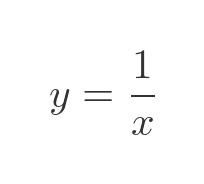
This function is plotted here. We are only interested in the function for values of x of 1 or greater:

When x gets larger, the value of the function gets smaller, but of course, it never reaches 0. Now consider what happens if we rotate this shape around the x-axis to form a surface of revolution:

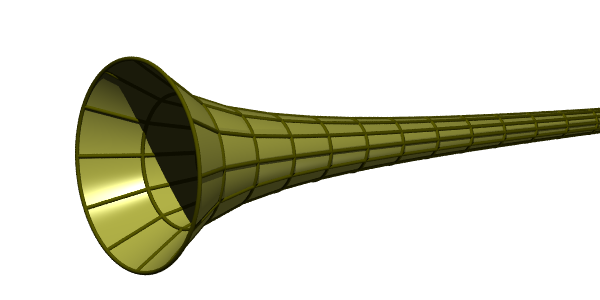
This creates a horn shape (properly called an acute hyperbolic solid). Just like the curve, the horn is infinitely long. The diameter gets narrower and narrower but never reaches 0.

The strange properties of Gabriel's horn

The horn is infinitely long, and it also has an infinite surface area. That isn't particularly surprising it is what you might expect from an infinitely long solid shape.

It also has a finite volume. This might be a little more surprising, but it arises because the formula for the volume converges as x gets larger.

There are a couple of interesting proofs of this result, but we won't look at them here. That will be a topic for a future article.

The painter's paradox

Since Gabriel's horn has a finite volume, we could fill it with paint. That would take a finite amount of paint.

When the horn is full of paint, then there will be paint covering the whole inner surface of the horn.

However, the surface area of the horn is infinite.

So we have painted an infinite area with a finite amount of paint! That is surely impossible?

Resolving the paradox

To resolve the paradox, it is helpful to consider a simpler 3D geometry. Let's imagine an empty cube-shaped box, with a lid, perhaps made of metal or glass, that we can fill with paint:

It doesn't matter how big the box is, but to help visualise it, let's assume the internal length, width, and height are 0.1 m (ie 10 cm). So the internal volume of the box is:

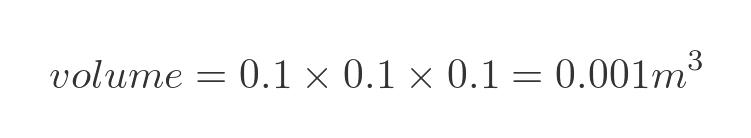
This is exactly 1 litre of paint.

What about the surface area of the inside of the box? It has 6 faces, each 0.1 m square, so its internal surface area is

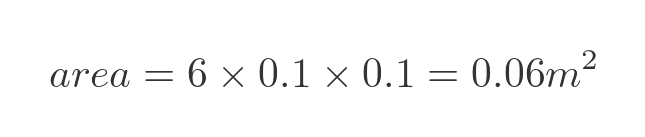
Changing the shape of the box

So now let's change the shape of the box, making the base larger and reducing the height, so that the volume is still the same:

We will make the width and height both 1 m, which is 10 times bigger than before. To keep the volume the same we need to shrink the height by a factor of 100. This makes the new height 0.001 m (ie 1 mm). The volume is still the same:

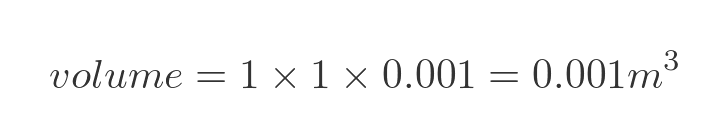
The internal surface area is different though. the top and bottom are 1 m by 1 m, and the 4 sides are 1 m by 0.001m:

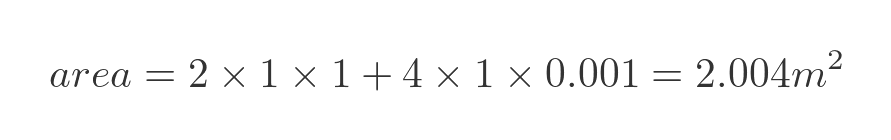
This all seems quite reasonable. Let's image the lid of the box can be removed. This would leave a tray, 1 m square and 1 mm deep. If we took a litre of paint and poured it into the tray, it would fill it to the brim. If we put the lid back on the box, the paint would cover the whole inner surface of the box. No problem.

What if we change the box shape again? This time we make the box 10m square, and reduce the height by a factor of 100 again:

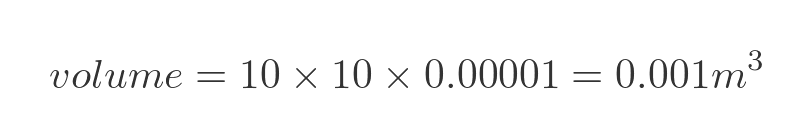
For the new surface area, the top and bottom are 10 m by 10 m, and the 4 sides are so small that we can safely ignore them:

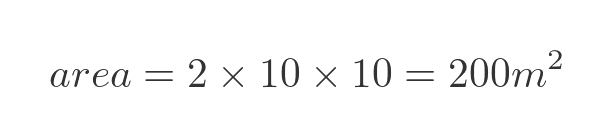
We need to take a quick sanity check here. If you have ever painted a wall, you will probably know that a litre of paint is probably not going to cover 200 square metres! As a rule of thumb, you would expect to cover about 10 square meters.

But let's assume we have some special paint, that is particularly thin and fluid. If we poured it into a tray that was 10 m square, maybe it would just about cover the tray.

Then, if we placed the lid on it, our paint would indeed be covering 200 square metres!

There is another problem though. The internal height of the box is 0.00001 m, which is 0.01 mm. How would we create a box, 10 m square, where the top and bottom are separated by just 0.01 mm? The top and bottom would need to be extremely flat and rigid, otherwise the top and bottom would touch in places, so the surface would not be completely covered. Again, let's assume we have a solution to that problem that allows us to carry on making our box even wider.

Physical limits

If we continue to increase the size of the box's base and decrease its height, we will pretty soon hit some hard physical limits.

Paint is usually a mixture of at least 3 different chemicals - the pigment that gives it its colour, a solvent that makes it liquid, and a binder that glues the pigments to the surface when the solvent evaporates off.

If we made the top and bottom 500 m by 500 m, the height would be 4 nanometres. Some of the individual molecules in the paint might be around that sort of size, which means that the paint will no longer be a mixture of molecules, it will just be isolated molecules of the various substances that form the paint. So you might ask, is it still paint?

What if we make the box base a few kilometres square? In practical terms that is ridiculous of course, but to paraphrase Douglas Adams that's just peanuts compared to infinity.

The height of the inside of the box would then be smaller than the diameter of a hydrogen atom. The top and bottom of the box will be as close together as they can be. The box no longer has an inside, so the surface area of the inside no longer exists. The paint would just exist as impurities inside a solid block of metal.

Resolution of the paradox

There is no mathematical paradox here. If we are dealing with mathematically perfect objects that are perfectly smooth and can be perfectly positioned infinitesimally close to each other, and mathematically perfect paint that can be spread evenly at sub-atomic or even sub-quantum thicknesses, then a finite amount of paint can cover a surface even as the surface area tends to infinity.

The reason it appears to be a paradox is due to 2 effects. First, we find it quite difficult to visualise and accept the idea that Gabriel's horn has finite volume but infinite surface area. This concept is easier to accept in the case of a very wide, very short box shape.

Secondly, we intuitively know that real paint can only be spread so far. If we poured real paint into Gabriel's horn, at some point the internal diameter of the horn would be so narrow that the paint wouldn't flow any further. And even if it was very thin paint, the diameter would eventually become too small for the individual molecules that make up the paint to pass through.

These limitations don't apply to the mathematical shape, but we might still be inclined to apply our physical intuitions to it, resulting in an apparent paradox.

See also

• Monty Hall problem
• Pigeonhole principle
• Drunk man and keys problem
• Raven paradox
• Potato paradox
• Russell's paradox
• Coin rotation paradox