Galileo's paradox
Categories: recreational maths paradox
Galileo's paradox investigates infinite sets. In particular, it looks at a case where common sense seems to tell us that one infinite set is smaller than another, but logic tells us they must be the same size.
Galileo considered the set of square numbers {1, 4, 9, 16 ...}. He compared this with the set of natural numbers {1, 2, 3, 4 ...}.
Clearly, both sets are infinite, because they both carry on forever. There is no largest square number, and there is no largest natural number. But also notice that the set of square numbers is a subset of the set of natural numbers. That is to say, every square number is a natural number, but not every natural number is a square number.
Here are the first few natural numbers, with the square numbers marked in bold:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59
This shows, of course, that most natural numbers are not squares. Also, as the numbers get larger, the gap between the squares gets greater and greater. Squares 1 and 4 are separated by two non-squares, but squares 36 and 49 are separated by twelve non-squares.
Based on this information, we are surely justified in saying that there are more natural numbers than there are square numbers. That is obvious. Isn't it? Well, perhaps not.
The paradox
Galileo noticed a problem with this logic. Every square number can be uniquely associated with a particular natural number ... its own square root:
- The square root of 1 is 1
- The square root of 4 is 2
- The square root of 9 is 3
- The square root of 16 is 2
- and so on:
This means there is a one-to-one correspondence between the square numbers and the natural numbers. And if there is a one-to-one correspondence between the members of the two sets, surely they must have the same number of elements?
Galileo's resolution of the paradox
Galileo concluded that the concepts of less, equal or greater cannot be applied to infinite sets. He was sort of right, but modern set theory gives us a better explanation.
Modern set theory
Cantor developed this idea further. He showed that two sets are equinumerous (ie the same size) if their elements can be paired, one-to-one. So the one-to-one mapping between the squares and the natural numbers proves that the two sets are the same size.
Many sets have this property. For example, the set of even numbers 2, 4, 6, 8 ... can be mapped onto the set of rational numbers 1, 2, 3, 4 ... simply by dividing by 2 (2 maps onto 1, 4 maps onto 2, and so on). This means that the set of even numbers is the same size as the set of natural numbers, which we have previously seen is also the same size as the set of square numbers. All three sets are the same size.
There is a special name for sets that map onto the natural numbers. We call them countable sets. As we have seen, all countable sets are the same size.
It isn't always obvious that a particular might be countable. For example, consider the set of all number pairs of the form (n, m), where n and m are integers. That includes (0, 0), (1, 2), (-2, 3) etc. The pairs are marked as points on this grid:
It isn't immediately obvious how we map these points onto the natural numbers since the grid extends to infinity in every direction. But in fact, we can visit the points in order by starting at (0, 0) and spiralling around, as shown here:
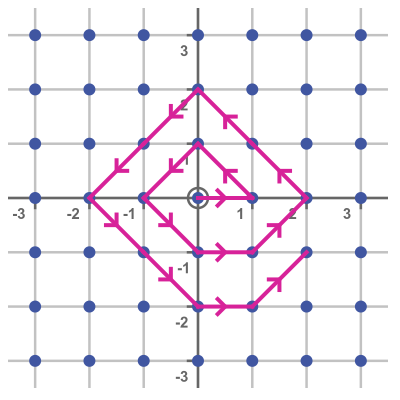
We can assign each point a unique natural number, which means the set is countable, and so has the same number of elements as the set of square numbers.
Non-countable sets
Not all infinite sets are countable. For example, the set of all real numbers is not countable. The set of natural numbers is infinite, and the set of real numbers is infinite, but the set of real numbers is infinitely bigger than the set of natural numbers.
See also
Join the GraphicMaths Newletter
Sign up using this form to receive an email when new content is added:
Popular tags
adder adjacency matrix alu and gate angle answers area argand diagram binary maths cartesian equation chain rule chord circle cofactor combinations complex modulus complex polygon complex power complex root cosh cosine cosine rule countable cpu cube decagon demorgans law derivative determinant diagonal directrix dodecagon eigenvalue eigenvector ellipse equilateral triangle euler eulers formula exercises exponent exponential exterior angle first principles flip-flop focus gabriels horn gradient graph hendecagon heptagon hexagon horizontal hyperbola hyperbolic function hyperbolic functions infinity integration by parts integration by substitution interior angle inverse hyperbolic function inverse matrix irrational irregular polygon isosceles trapezium isosceles triangle kite koch curve l system line integral locus logarithm maclaurin series major axis matrix matrix algebra mean minor axis n choose r nand gate net newton raphson method nonagon nor gate normal normal distribution not gate octagon or gate parabola parallelogram parametric equation pentagon perimeter permutations polar coordinates polynomial power probability probability distribution product rule proof pythagoras proof quadrilateral questions radians radius rectangle regular polygon rhombus root sech segment set set-reset flip-flop sine sine rule sinh sloping lines solving equations solving triangles square square root standard curves standard deviation star polygon statistics straight line graphs surface of revolution symmetry tangent tanh transformation transformations trapezium triangle turtle graphics uncountable variance vertical volume volume of revolution xnor gate xor gate