Algebraic and transcendental numbers
Categories: number theory

An algebraic number is any number that is a root of some polynomial with integer coefficients. A transcendental number is any number that is not algebraic.
In this article, we will unpack those definitions, look at some of the properties of both types of numbers, and see how they are useful in various branches of mathematics. We will only consider real numbers here, but the concept applies equally to complex numbers.
Definition of algebraic number
As we noted above, an algebraic number is any number that is a root of some polynomial with integer coefficients (sometimes called integer polynomials). That is to say, any number that is a solution to an equation like this is algebraic:
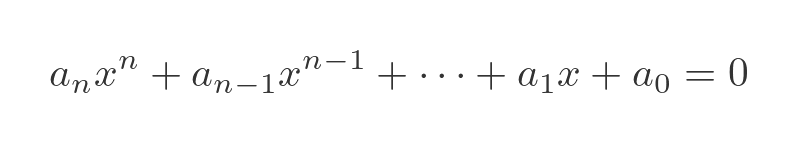
All the coefficients must be integers, which of course includes positive and negative values, and zero. We write that like this in maths notation, stating that the coefficients are members of Z, the set of integers:

Notice that we have also specified that the highest order coefficient, a_n, cannot be zero. That is simply because, if that coefficient is zero, we will miss the term out altogether and write it as a lower-order polynomial. For example, a cubic polynomial with a zero cubic coefficient is simply a quadratic polynomial:

Simple examples of algebraic numbers
What are some examples of algebraic numbers? We can start by looking at the roots of various simple integer polynomials. Any root of any such polynomial will be an algebraic number by definition.
First, we will look at a first-order polynomial (ie a linear equation), where a is an integer:
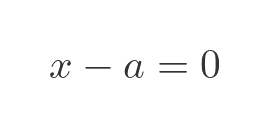
This has a solution x = a, and by definition, this means that a is an algebraic number. Since a can be any integer, this means that all integers are algebraic numbers.
Here is another case:
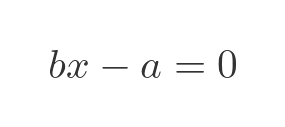
This has a solution x = a/b, where a and b are integers and b is not zero. This means that all rational numbers are algebraic. For example, 1/2 or -22/3 are algebraic.
What about quadratic polynomials? Here is a simple case:
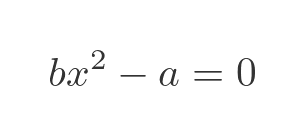
We can solve this for x squared:

Now this equation only has a real solution when a/b is positive (ie, a and b have the same sign), but in that case, both the positive and negative square roots are solutions:
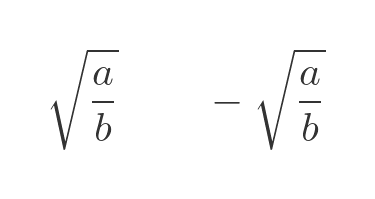
This means that the square root of any rational number is algebraic. Since this includes the special case when b is 1, so a/b is an integer, it means that the square root of any integer is also algebraic.
We can do the same thing with a simple cubic polynomial:
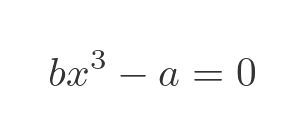
This time, of course, the root of the polynomial is a cube root.
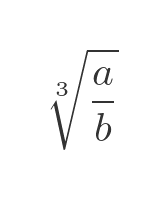
This time, a and b do not need to be the same sign, because we can find the cube root of a negative number. This means that the cube root of any rational number (and also any integer, of course) is an algebraic number.
We won't show it here, but it is hopefully fairly clear that the logic above doesn't only apply to square roots and cube roots. In general, the nth root of any rational number is algebraic. Again, that includes integers.
Further examples of algebraic numbers
Rational numbers and roots of rational numbers are algebraic. What about the sum of a number and a root?
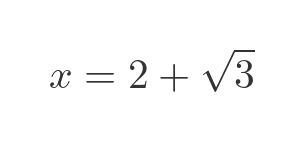
This looks like it might be the root of a quadratic equation (based on the standard quadratic formula). We can check that by creating an integer polynomial that has the value above as a root. To do this, we need to eliminate any roots from the coefficients of the polynomial. We can start by finding x squared:

If we subtract 4x from x squared, the root term will cancel, leaving just an integer value:
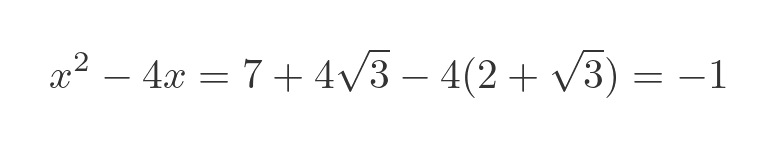
So we can say that:
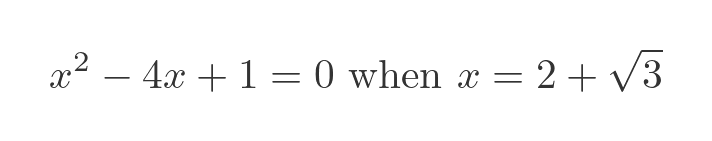
So our original term, the sum of a number and a root, is the solution to this particular quadratic equation, so it is an algebraic number.
We won't prove it here, but we could perform a similar manipulation of any rational plus the root of a rational, to demonstrate that it is an algebraic number. Furthermore, we could take any expression involving only rational numbers, roots, and basic arithmetic operations, and manipulate it to find an integer polynomial that it solves. This gives us the general rule:
Any expression that uses only rational numbers, integer roots and powers, addition, subtraction, multiplication, and division will be an algebraic number.
Any number that obeys that rule will be algebraic, but as we will see, not every algebraic number obeys that rule.
Unsolvable algebraic numbers
The well-known quadratic formula can be used to solve any quadratic equation. And, due to the form of the equation, we know that, if a, b and c are integers, the solutions will be algebraic. There are similar equations to find the roots of cubic and quartic equations (ie polynomials where the highest power of x is 3 or 4).
There is no such formula for polynomials of order 5 (quintic) and above. It is sometimes possible to factorise a quintic equation, for example:
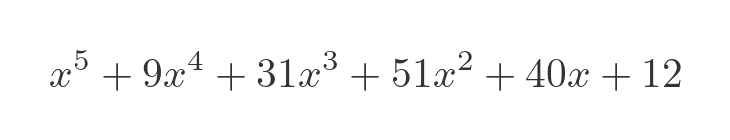
Can be factored out as:
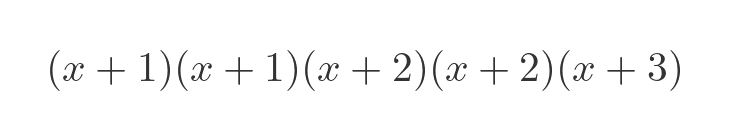
But sometimes that is not possible, for example:
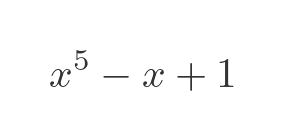
There is no known exact factorisation of this polynomial. That means that we cannot express the roots of the equation as exact numbers obeying the general rule above.
If the function cannot be factorised exactly, does that mean it has no roots? Well, we can easily plot the function to find out, and yes, it does have one real root:
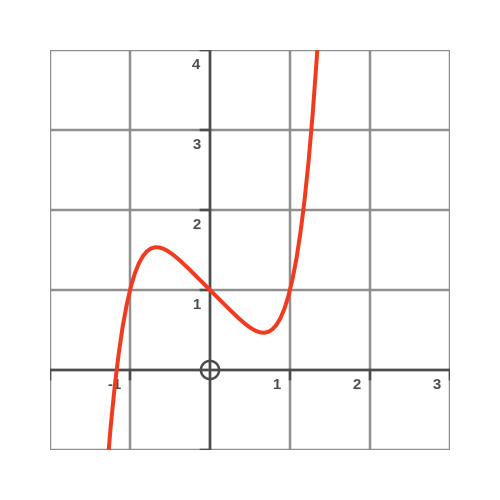
It has a real root at approximately -1.1673. It also has four complex-valued roots, at approximately 0.7649 ± 0.3525i and -0.1818 ± 1.08340i.
Do these numbers count as algebraic numbers? Well, yes, of course, they are the roots of an integer polynomial, so they are algebraic by definition. We just can't express them in terms of basic algebraic operations on integers.
So let's update our previous rule:
Any expression that uses only rational numbers, integer roots and powers, addition, subtraction, multiplication, and division will be an algebraic number, BUT not every algebraic number can be expressed using only rational numbers, roots, addition, subtraction, multiplication, and division.
So, how do we find the roots?
How do we find the roots of an unsolvable quintic? Well, we can't, not exactly. We can only use numerical methods to find an approximate value. For example, we can use interval bisection where we try x different values close to -1.6 and gradually home in on a value of x that gives a result that is closer and closer to zero. Or instead, we could use Newton's method, which is a different type of iterative method that often converges a lot faster.
That might seem like an unsatisfactory method. But if you think about it, that is what we do in a lot of other cases. For example, suppose we know the solution to an equation is the square root of 2. We have given the value a name, but what is its actual, numerical value? Nobody knows the exact value of the square root of two, because it is an irrational number. All we can do is calculate its approximate value. Usually using Newton's method, or similar. That is no different from finding the approximate roots of an unsolvable polynomial.
The set of algebraic numbers is countable
We can describe infinite sets as either being countable or uncountable. The set of all integers is infinite, but countable. The set of all real numbers is uncountable. But what about the set of algebraic numbers? We know that every algebraic number is a root of an integer polynomial. Can we count those roots?
Let's break this problem down a little. So, we will start by considering only polynomials of order 1:
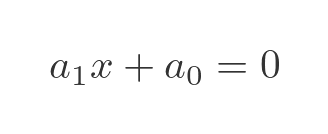
The coefficient a0 is an integer, so the set of possible values of a0 is countable. The same is true of a1.
There is a rule that the Cartesian product of a finite number of countable sets is itself a countable set. That means that the set of all possible pairs (a0, a1) is countable. That means that the total number of different integer polynomials of order 1 is countable. And since each polynomial has one solution, that means that the total number of solutions (ie algebraic numbers) is countable.
Next, we will consider only polynomials of order 2:
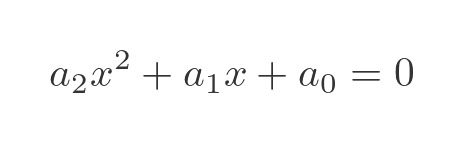
Each coefficient (a0, a1, and a2) is countable, so again the set of all possible triplets (a0, a1, a2) is countable. Since each triplet corresponds to a unique polynomial, and each polynomial has at most two solutions, the number of solutions is countable.
We can apply the same logic to polynomials of order 3, 4, and so on. The number of solutions for all the polynomials of any particular size is countable.
There is another rule that the union of any countable set of countable sets is also a countable set. We have looked at polynomials of order 1, 2, 3, 4, etc. There is a countable set of polynomial orders, and each polynomial order is associated with a countable set of possible solutions of polynomials of that order. So that means the set of all possible solutions to any integer polynomial is countable.
So the set of all algebraic numbers is countable.
Transcendental numbers
As we saw earlier, any number that isn't algebraic is transcendental. Put another way, a transcendental number is any number that isn't a root of any integer polynomial.
In the early days of studying algebraic numbers, it wasn't particularly obvious whether transcendental numbers even existed. There are so many ways to create algebraic numbers by combining any number of rational numbers and irrational roots. Who is to say that we can't form every possible real number from some such combination?
As an aside, we now know that the set of algebraic numbers is countable, and the set of real numbers is uncountable, and since an uncountable set is larger than a countable set, there must be real numbers that are not algebraic (ie are transcendental). But that knowledge comes from Cantor, who wasn't even born when the initial work on transcendental numbers was being done.
But even if we know that transcendental numbers exist, finding them seems quite daunting. We have to prove that the number cannot be the root of any possible integer polynomial. It took a great deal of ingenuity to do that, and there are still some numbers that are almost certainly transcendental, but nobody has yet managed to prove it.
We won't cover any of the proofs in detail here, they will be the subject of a later article.
The Liouville constant
The first proven transcendental number was the Liouville constant, devised by Joseph Liouville. This was a special number that had been deliberately designed so that it could be proven to be transcendental. The number is defined as:

To understand this number, let's look at the first few terms:
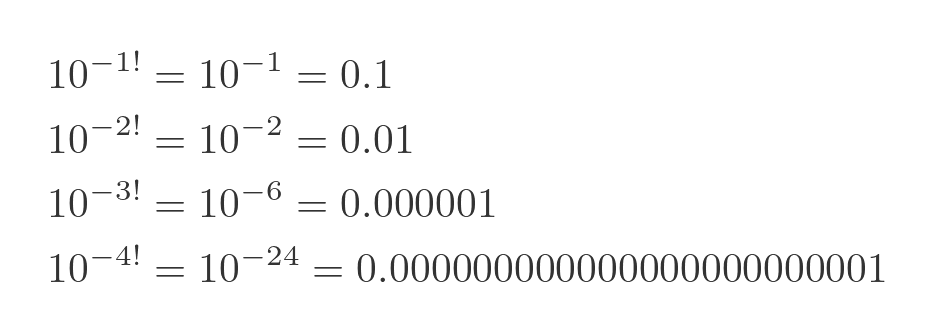
Each term is 10 to the power -n!, with a decimal with all 0s except a 1 in the n! decimal place. So the first term has a 1 in dp 1, the second has a 1 in dp 2, the third in dp 6, and the fourth in dp 24. When we add all these together, we get a decimal fraction that is mainly zeros, with a 1 every so often.
The factorial term gets very big, very quickly, so the number of 0s between each 1 gets larger and larger as we progress. For example, 10! is 3,628,300. So the tenth term is a decimal point followed by more than three million 0s, and then 1.
We won't go through the proof here, that is for another article. To give a brief outline, we define Ln as being L truncated to n decimal places. It can be shown that if L is the solution to some integer polynomial, the Ln will also be a solution to that same polynomial, provided n is large enough. This arises because the ones get more and more sparse as we include more decimal places, so at some point, if we truncate those decimal places, the resulting Ln is still a solution. Since all Ln are solutions if n is big enough, there are infinitely many solutions. But a polynomial can only have a finite set of solutions, so L cannot be a solution to any integer polynomial.
Transcendental mathematical constants
The well-known constants π and e (Euler's number) have both been proved to be transcendental. Several mathematical combinations have also been proved to be transcendental, including e to the power of π, and also e to the power of a where a is any algebraic number (except 0). These numbers are transcendental:

There are other, similar combinations of π and e that have not been proved to be transcendental. That doesn't mean they are not transcendental; many people think that they are. But so far, nobody has found proof for these cases:
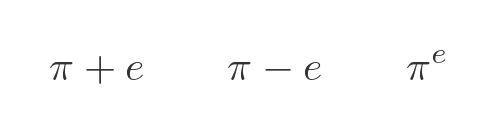
Hilbert's number
Hilbert's number is interesting because it contains only integers and square roots:
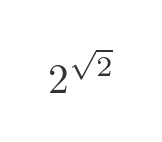
Why isn't this number algebraic? Well, if you recall, a number is guaranteed to be algebraic if it consists only of rational numbers and roots that are combined using addition, subtraction, multiplication, and division.
In this case, 2 is raised to the power of root 2, and powers are not an allowed operation. Raising to an integer power is permitted because that can be expressed as multiplication, but raising to an irrational power is not.
This alone doesn't prove the solution is transcendental; it only indicates that it might be. However, Hilbert proved that it is, and the number was named after him.
i to the power i
This article only deals with real numbers. However, we can perhaps make a special case for i raised to the power i (where i is the imaginary unit). That is because, somewhat surprisingly, this expression has a real number value:
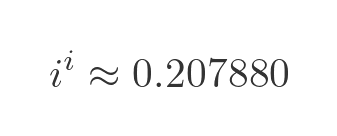
It can be shown that this number is also transcendental.
The set of transcendental numbers is uncountable
We know that every real number is either algebraic or transcendental. We previously proved that the set of algebraic numbers is countable. What about the set of transcendental numbers?
For brevity, we will make use of some well-known facts about sets and numbers, without proof. The first is that the set of real numbers is uncountable. That is, unlike the set of algebraic numbers, the set of reals cannot be arranged in order and counted. There are infinitely many algebraic numbers, but there are far, far more reals.
Our second fact is that if you have an uncountable set (the real numbers) and remove a countable set of values (the algebraic numbers), the remaining set is still uncountable. In our case, when we remove the countable set of algebraic numbers from the uncountable set of real numbers, we are left with the set of transcendental numbers.
This proves that the set of transcendental numbers is uncountable.
This is a little counterintuitive. We all know lots of algebraic numbers - all the integers, all the fractions, all the square roots and cube roots of all those previous numbers, and more. But the only transcendental numbers most people have heard of are π and (possibly) e.
But in fact, almost every number is transcendental. It is the algebraic numbers that are, comparatively, extremely rare.
Related articles
Join the GraphicMaths Newsletter
Sign up using this form to receive an email when new content is added to the graphpicmaths or pythoninformer websites:

Popular tags
adder adjacency matrix alu and gate angle answers area argand diagram binary maths cardioid cartesian equation chain rule chord circle cofactor combinations complex modulus complex numbers complex polygon complex power complex root cosh cosine cosine rule countable cpu cube decagon demorgans law derivative determinant diagonal directrix dodecagon e eigenvalue eigenvector ellipse equilateral triangle erf function euclid euler eulers formula eulers identity exercises exponent exponential exterior angle first principles flip-flop focus gabriels horn galileo gamma function gaussian distribution gradient graph hendecagon heptagon heron hexagon hilbert horizontal hyperbola hyperbolic function hyperbolic functions infinity integration integration by parts integration by substitution interior angle inverse function inverse hyperbolic function inverse matrix irrational irrational number irregular polygon isomorphic graph isosceles trapezium isosceles triangle kite koch curve l system lhopitals rule limit line integral locus logarithm maclaurin series major axis matrix matrix algebra mean minor axis n choose r nand gate net newton raphson method nonagon nor gate normal normal distribution not gate octagon or gate parabola parallelogram parametric equation pentagon perimeter permutation matrix permutations pi pi function polar coordinates polynomial power probability probability distribution product rule proof pythagoras proof quadrilateral questions quotient rule radians radius rectangle regular polygon rhombus root sech segment set set-reset flip-flop simpsons rule sine sine rule sinh slope sloping lines solving equations solving triangles square square root squeeze theorem standard curves standard deviation star polygon statistics straight line graphs surface of revolution symmetry tangent tanh transformation transformations translation trapezium triangle turtle graphics uncountable variance vertical volume volume of revolution xnor gate xor gate
