Permutations
Categories: statistics probability

Imagine we have 4 cards, numbered 1 to 4, and we place them on a table, side by side:
We can arrange those same 4 cards in a different order, for example:
Each different way of ordering the cards is called a permutation of the set of cards.
A permutation is a particular set of items in a particular order.
Number of permutations of n objects
How many different permutations are possible? With 4 different cards there are 24 different permutations:
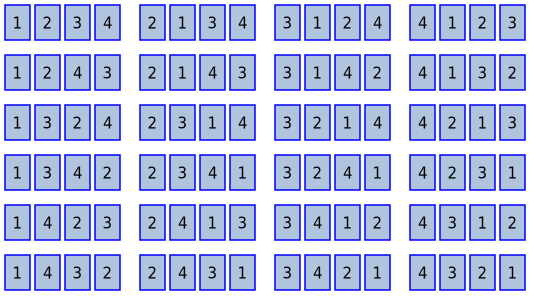
This only applies if all the cards are different. We will look at other cases later.
To understand why there are there 24 combinations, let's assume we start with the 4 cards and place them on the table, one by one. For the first card, we have 4 possible cards to choose from, so there are 4 possibilities for the first card:

For the second card, one card has already gone, so we have 3 possible cards to choose from. For each of the 4 possible first cards, there are 3 possible second cards, so there are a total of 12 possibilities for the first 2 cards:
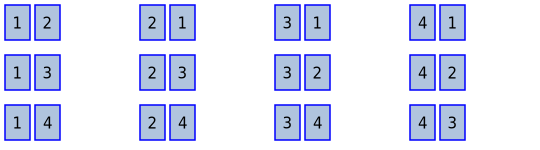
For the third card, two cards have already gone. We only have 2 cards left to choose from. For each of the 12 possible pairs of cards from the previous step, there are 2 possible third cards, so there are a total of 24 possibilities for the first 3 cards:
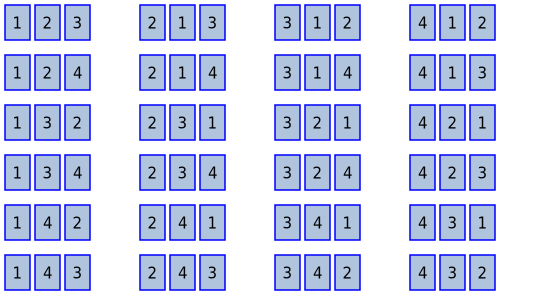
There is now only one card left, so we have no choice which card to use as the final card. This means that there are 24 possible permutations of the four cards, as shown in the first diagram above.
For 4 cards the number of permutations is:
$$ 4 \times 3 \times 2 \times 1 = 24 $$
This is, of course, 4 factorial. This is often written as 4!
In general, the number of permutations of n unique items is n factorial:
$$ n \times (n - 1) \times ... \times 2 \times 1 = n! $$
Number of permutations of r items selected from n items
Next, we will look at a slightly different case. We have n items, but we will only select r of those items.
For example imagine we have 5 different coloured counters - red, yellow, green, blue, and black. We will select 2 of those counters.

We might choose:
- A red counter then a yellow counter.
- A green counter then a white counter.
- A yellow counter then a red counter.
How many permutations of 2 counters are there?
The first thing to be clear here is that we are still looking at permutations, so the order is important. A red counter then a yellow counter is not the same as a yellow counter then a red counter. They are considered to be different cases.
Following the same logic as the previous section, we have 5 choices for the first counter, then 4 choices for the second counter. So the number of permutations is:
$$ 5 \times 4 = 20 $$
These are the first 2 terms of 5 factorial (that isn't surprising, based on the previous section - it is just the first two stages of calculating the total number of permutations).
In general, the number of permutations of r items from n is given by the first r terms of n factorial. However, this can be expressed more succinctly as:
$$ \frac {n!}{(n-r)!} $$
This illustration shows why:
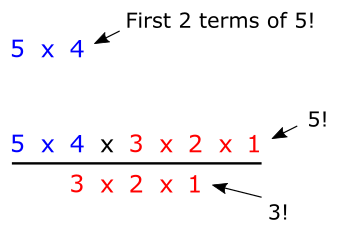
If we divide 5 factorial by 3 factorial, the last 3 terms cancel out, so we are left with just the first 2 terms, which is exactly what we want. In general, n! divided by (n - r)! with give the first r terms of n!.
Permutations of n items with repetition
In some situations, items in the permutation are allowed to be repeated. Consider the case of a Personal Identification Number (PIN), which might be used to access a cash machine. This is often a 4 digit number. A PIN can contain repeated digits, for example 1662.
How many possible 4 digit PINs are there? This is a permutations question because the order of the digits matters (for example 1662 and 6261 are different PINs). But unlike the card example, the same digit can be repeated. So:
- The first digit can be any number from 0 to 9, so there are 10 possibilities.
- The second digit can also be any number from 0 to 9, so there are 10 possibilities.
- Similar for the third and fourth digit, of course.
So the total number of permutations is:
$$ 10 \times 10 \times 10 \times 10 = 10^4 = 10000 $$
Generally, the number of permutations of r items from n when repetitions are allowed is:
$$ n ^ r $$
Permutations with repetition are often used where an item is chosen and then put back so it can be chosen again. For example, if you have a deck of ordinary playing cards:
- If you shuffle the deck and deal 3 cards that is a simple permutation. The same card can't appear twice.
- Alternatively you might shuffle the deck and deal card 1 then put it back in the deck. Shuffle again and deal card 2, then but it back. Shuffle again and deal card 3. In that case, it is possible (though quite unlikely) that the same card is drawn twice or even three times, so the number of permutations must be calculated as a permutation with repetition.
Permutations from a set with non-unique members
So far we have only considered a set of unique items. What if we had a set of items where some were identical? For example:
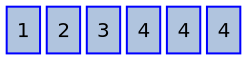
Here there are 7 cards, but 3 of them have the value 4.
There are 7! ways to arrange the cards, but not all of those ways are unique. Consider this case:
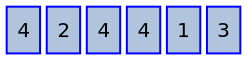
If we swapped two of the cards that have a number 4, the permutation of numbers would be unchanged. The actual cards would have been swapped, but since they are identical that would make no difference. Since there are 3 identical cards, there are 3! different permutations of those cards.
In other words, for every unique permutation of numbers there are 3! different permutations of cards. So we must divide the number of permutations of cards by 3! to find the number of unique permutation of numbers.
This means that the number of different permutations of the 7 cards is:
$$ \frac {7!}{3!} = 840 $$
In general, if you have n objects, but c of them are identical, the number of permutations is:
$$ \frac {n!}{c!} $$
Permutations from a binary set
There is a special case when the set only contains two distinct types of items. For example, if we had a set of counters that were all either red or blue:

In this case, there are 8 counters, so there are 8! possible permutations of the counters. But because there are 5 red counters, we must divide the total by 5!, as we did before. And because there are 3 blue counters, we must also divide the total by 3! for the same reason. So the total number of unique permutations of the red and blue counters is:
$$ \frac {8!}{5!3!} = 56 $$
In general, if you have n items, where c are of type A and the rest are of type B, the number of unique permutations is:
$$ \frac {n!}{c!(n-c)!} = 56 $$
Related articles
Join the GraphicMaths Newsletter
Sign up using this form to receive an email when new content is added to the graphpicmaths or pythoninformer websites:

Popular tags
adder adjacency matrix alu and gate angle answers area argand diagram binary maths cardioid cartesian equation chain rule chord circle cofactor combinations complex modulus complex numbers complex polygon complex power complex root cosh cosine cosine rule countable cpu cube decagon demorgans law derivative determinant diagonal directrix dodecagon e eigenvalue eigenvector ellipse equilateral triangle erf function euclid euler eulers formula eulers identity exercises exponent exponential exterior angle first principles flip-flop focus gabriels horn galileo gamma function gaussian distribution gradient graph hendecagon heptagon heron hexagon hilbert horizontal hyperbola hyperbolic function hyperbolic functions infinity integration integration by parts integration by substitution interior angle inverse function inverse hyperbolic function inverse matrix irrational irrational number irregular polygon isomorphic graph isosceles trapezium isosceles triangle kite koch curve l system lhopitals rule limit line integral locus logarithm maclaurin series major axis matrix matrix algebra mean minor axis n choose r nand gate net newton raphson method nonagon nor gate normal normal distribution not gate octagon or gate parabola parallelogram parametric equation pentagon perimeter permutation matrix permutations pi pi function polar coordinates polynomial power probability probability distribution product rule proof pythagoras proof quadrilateral questions quotient rule radians radius rectangle regular polygon rhombus root sech segment set set-reset flip-flop simpsons rule sine sine rule sinh slope sloping lines solving equations solving triangles square square root squeeze theorem standard curves standard deviation star polygon statistics straight line graphs surface of revolution symmetry tangent tanh transformation transformations translation trapezium triangle turtle graphics uncountable variance vertical volume volume of revolution xnor gate xor gate
