Zermelo-Fraenkel set theory

In this article, we will look at Zermelo-Fraenkel set theory, why it is necessary, and what it is. And as an example, we will see how it can be used to define the set of natural numbers.

Naive set theory

Up until the start of the 20th century, a mathematical set was defined according to what we now call naive set theory (it wasn't called that at the time, of course, because nobody had realised the problem with it). Loosely speaking, naive set theory says a set can contain any group of things that share a particular property, and that property can be described using natural language.

More formally, we say that for any property P(x) that is either true or false, we can form a set of all values of x for which P(x) is true. This is called the axiom of unrestricted comprehension, which is just a formal way of saying that a set can be constructed from any property P.

So for example, the set of all natural numbers less than 4 is the set {1, 2, 3}. The members don't have to be numbers. We could define a set of all the vowels in the English language, which would be {A, E, I, O, U}.

A set can be infinite, for example, the set of the natural numbers, N, is infinite. The set of even numbers, N2 would be {0, 2, 4, 6 ... } (we are counting 0 as a natural number, very much a matter of opinion, but we include the empty set as a set, so it is useful to include 0 as a natural number). That set is infinite, but we can easily calculate the nth element, it is simply 2n. So if we wanted to know element number 1e100 (that is 1 followed by 100 zeros) the answer would just be 2e100.

Another infinite set is the set of prime numbers, {2, 3, 5 7 ... }. This again is a valid set, but calculating element number 1e100 would be very difficult because we would have to calculate every prime number leading up to the one we wanted. Despite this practical problem, we can certainly say that there is an element 1e100.

This all seemed perfectly reasonable until the cracks started to appear.

Russel's paradox

The problem with naive set theory is that it leads to paradoxes. The most famous of these is Russel's paradox published by Bertrand Russel in 1901.

Since sets can contain anything, it is possible to define a set that contains other sets, and we can specify that set of sets in any way we wish. For example, we know that some sets are infinitely large, so we could define a set I containing every infinitely large set. This would include (amongst other things) the set of all natural numbers, the set of even natural numbers (N2), the set of natural numbers that are divisible by 3 (N3), and so on.

The are infinitely many sets of natural numbers that are divisible by some number n, so the set I is infinite in size. So I would be a member of itself. Which is absolutely fine in naive set theory, there is no reason why a set can't be a member of itself.

So now we know that some sets, such as I, are members of themselves. And of course some other sets, such as the set of natural numbers N, are clearly not members of themselves (N only contains numbers, not sets, so it cannot contain itself).

So we can define another property of sets: "does not contain itself". This is a valid property of sets - we will call this property C(x). The property is true of some sets (such as N) that do not contain themselves. And it is false of other sets (such as I) that do contain themselves. So according to naive set theory, we can define a set R of all sets that do not contain themselves.

But there is a problem. If R does not contain itself, then C(R) is true so it must contain itself. But if R contains itself, then C(R) is false so it cannot contain itself. This is a paradox. And it is not a trivial paradox that can be ignored. This is a genuine paradox at the heart of naive set theory, and there is no logical way out of it.

Cantor's paradox

Another paradox concerns the universal set, U. that is the set of all possible sets.

To understand this paradox, we need to define the power set. The power set Y of a set X is the set of all subsets of X including the empty set. So for example the power set of the set {1, 2, 3} would be:

{{}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}

There are two important properties of a power set:

• All its members are sets.
• It always has more members than the original set.

The second property arises because the power set contains a member for each member of the original set (the values 1, 2, and 3 in the original set give rise to members {1}, {2}, {3} in the power set), plus an empty set, and usually a whole lot of extra subsets.

Here, a paradox arises when we take the power set pU of the universal set U.

We know that pU must be bigger than U, because the power set is always bigger than the original set. And we know that both U and pU sets only contain sets. So if pU is bigger, it must contain more sets than U.

But U contains every set, so how can Pu contain more sets than U? This is another unsolvable paradox in naive set theory.

Resolving the paradoxes

The root of these problems is the idea of unrestricted comprehension. It makes no sense to be able to define a set in any way we wish because some ways of describing a set using natural language do not make sense mathematically. In particular, we can't always define a set in terms of itself.

The Zermelo-Fraenkel (ZF) set theory is based on a set of axioms that avoid this problem. They essentially only allow us to create new sets in terms of sets that already exist, so avoiding any self-referential paradoxes. The scheme goes further than that. It says that sets can only contain other sets.

The theory usually includes an extra axiom, the axiom of choice, and is then described as ZFC. We won't look at the axiom of choice here, that will be a future article.

The ZF system contains nine axioms. There are several basic set rules, plus a bunch of axioms that specify how we can construct new sets from existing sets, followed by a couple of extra axioms that are slightly less straightforward.

Some basic rules

Since our approach is to only ever define sets in terms of other sets, how do we start? Well, we have to define at least one set that just exists. But a set can only be constructed from other sets, so need a set to already existing set before we can define our first set.

Fortunately there is such a set. The empty set, a set with no elements

The empty set exists is sometimes called axiom 0 of ZF. This states that the empty set can be assumed to exist. That is a pretty reasonable assumption. If sets exist at all, the empty set must surely exist.

The empty set is sometimes written as {}, but we will use another commonly used symbol, ∅ (this symbol isn't a Greek letter, it is the null sign, Unicode value U+2205). Oddly enough, we can define every set we need from this humble starting point.

The axiom of extent can be used to determine if two sets are the same. It states that two sets A and B are the same if and only if every element of A is an element of B, and every element of B is an element of A.

Another way of stating this is to say that a set is uniquely defined by its elements. This is the same rule we have always used - sets are equal if they contain exactly the same elements - just expressed more formally.

Rules for construction sets

There are several rules for creating sets from other sets. They are all quite simple and obvious, as axioms should be.

The axiom of pairing tells us that, if A and B are sets, then {A, B} is a set. That is, if we have two sets we can create a new set with two elements, which are the two original sets. For example we can combine the two sets {1, 2} and {5, 6} to create the set {{1, 2}, {5, 6}}.

A special case of this is that if A is a set then {A, A} is a set. We don't normally see a set with repeated elements. This is because the axiom of extent allows us to remove duplicate elements. The two sets {A, A} and {A} are the same set because every element of either set is also an element of the other set. So we normally just write {A}.

This gives us a second useful result from the axiom of pairing: If A is a set, then {A} is also a set.

The axiom of union tells us that, if A and B are sets, then the union of A and B is a set. That is, if we have two sets we can create a new set with all the elements from either of the sets. For example, we can combine the two sets {1, 2} and {5, 6} to create a new set {1, 2, 5, 6}. This is different to the pairing example because the new set has 4 elements rather than 2.

The axiom schema of replacement tells us that, if A is a set and we apply some function to each of its members, then the modified members will also form a set. For example, if we took the set {1, 2, 3} and applied the function multiply by 4 we would get a new set {4, 8, 12}.

The axiom of restricted comprehension says that if A is a set, then we can use any rule we like to construct a subset of A.

For example, if we have the set N of natural numbers {1, 2, 3 ... } we can apply the rule is even to construct the set of even numbers {2, 4, 6 ... }. This rule simply collects all the even numbers and discards all the odd numbers.

This contrasts with the rule of unrestricted comprehension, which allows us to create a set from nothing using any rule. Restricted comprehension only allows us to build a set by applying a rule to an already existing set.

The axiom of power sets tells us that if A is a set then the power set of A is also a set. We gave an example of the power set of {1, 2, 3} earlier.

The axiom of regularity

The axiom of regularity states that any non-empty set A must contain an element that is disjoint from A. Two sets are disjoint if they don't contain any of the same elements. In other words, the intersection of A and x must be empty for at least one x that is a member of A:

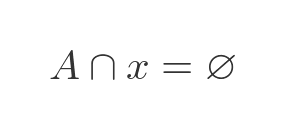
One of the main effects of this axiom is that it doesn't allow a set to be a member of itself. For example, in naive set theory, we could say that set A is the set that only contains the set A:

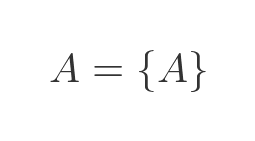
This is not allowed in ZF set theory because any set A must contain an element that is disjoint from A. But the only element in A is A, and A cannot be disjoint from A because they are both the same set. So, due to the axiom of regularity, it is impossible to have a set whose only member is itself.

But what about the set {A, B}? If B was disjoint from A, then wouldn't it be possible for A to equal {A, B}, which would then allow A to be a member of itself?

We can show that this is not possible, using proof by contradiction. Let's assume:

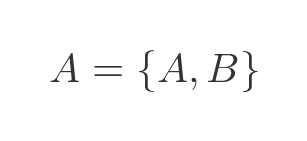
Since A is a set, by the pairing axiom {A} is also a set, and we can call this set C:

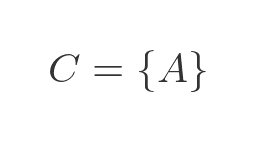
Using the previous logic we can use the axiom of regularity to say that C must contain an element that is disjoint from C, and since C only contains one element A, this means:

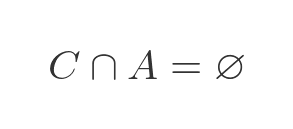
There is nothing wrong with that statement, of course. C and A are different sets, so saying they are disjoint is no contradiction.

But we also know how to express C and A in terms of A and B:

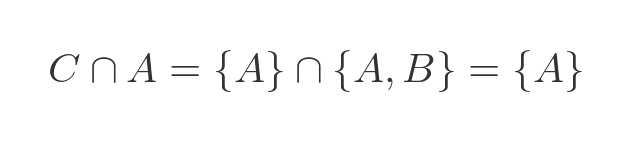
This yields a result that is incompatible with the axiom of regularity, and the reason it is incompatible is that we have defined A to contain A as a member. Therefore A cannot contain A as a member.

We have only proved this for A containing two elements, but the proof can be readily extended to a larger set. With a little more work we can also prove that cyclical sets cannot exist (ie if X contains Y, and Y contains Z, then Z cannot contain X).

The axiom of infinity

The axiom of infinity says that an infinite set exists that has elements that correspond to the natural numbers. This is important because it means that the ZF set theory can represent the natural numbers and as a consequence any other countable set.

Consider the rules above. We can only create a set based on existing sets, and our starting set is just the empty set. How can we create a set {1, 2, 3}? The number 1, for example, would need to already be a member of some existing set, but how can that be if our starting point is the empty set and nothing else?

What we will do is construct an infinite number of different sets, all based on the empty set. And those sets will have a natural order based on their structure. Then we can simply label each of those sets as being 0, 1, 2 etc. So the set of natural numbers will just be an infinite number of different sets based on ∅, but we can say that each of those sets represents a natural number. And, as a shorthand, we can write 0, 1, 2... in place of those sets.

We can use the empty set, ∅, to represent the number 0, that is quite easy. The empty set has zero elements, which is quite a good mnemonic. We will call this Set 0.

We can use the axiom of pairing to create a new set {∅, ∅}. We saw by the axiom of extent that this set can also be written as {∅}. It is important to note that this new set, the set containing the empty set, is completely different from the empty set itself. The empty set contains no elements, but this new set contains one element. So we could use {∅} to represent the number 1. We will call this Set 1. Notice that Set 1 has one element.

What if we pair Set 0 with Set 1? We get {∅, {∅}}. This set has two elements, so we could use it to represent the number 2 (and call it Set 2).

Another way of writing Set 2 is {0, 1} - we get this by substituting 0 for ∅ and 1 for {∅}.

Now we are on a roll! We represent the number 3 using Set 3, which contains the three elements {0, 1, 2}. In terms of the empty set, this set would be written as {∅, {∅}, {∅, {∅}}}. Following this pattern, we can create a unique set to represent every possible natural number.

Here are the first few natural numbers as sets:

Of course, these sets become ridiculously unwieldy for large numbers but that doesn't matter. We will always refer to Set 100 as 100, for instance. The real set is long and tedious, but we never need to write it down. Simply knowing that it exists and being able to create it in principle is all we require.

See also

• Countable and uncountable sets