The golden ratio

The golden ratio was mentioned in Euclid's Elements around 300 BCE, although it was probably known even earlier than that. It has been studied by mathematicians ever since.

At its simplest, we can say that two quantities are related by the golden ratio if the ratio between them is the same as the ratio between their sum and the largest of them. We can express this as a simple formula. Two numbers a and b (where a > b) are in the golden ratio if:

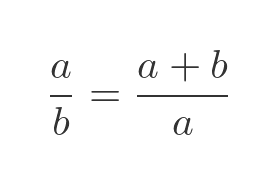
We can also show this as a diagram:

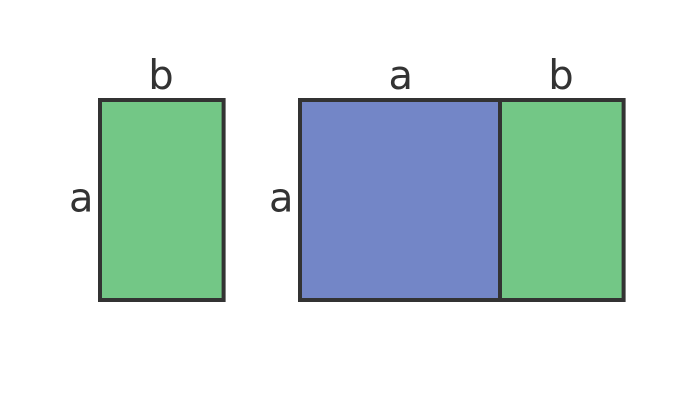
The first rectangle is size a by b, and the second is a + b by a. If a/b is the golden ratio then the two rectangles will be similar (in the mathematical sense of being the same shape but not necessarily the same size). We call this rectangle a golden rectangle.

Notice that the larger rectangle is formed by adding a square to the smaller rectangle. The two rectangles will only be similar if the original rectangle has sides in the golden ratio.

What is the value of the golden ratio?

Looking at the smaller rectangle, the value of the golden ratio is given by the long side divided by the short side (by convention, we do it that way round to get a value greater than one). We will call that ratio ϕ (the Greek letter phi):

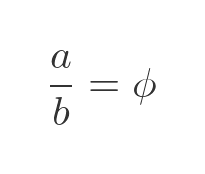
But how do we determine that value? Well, we know that the larger rectangle is the same shape, but this time its sides are a + b and a, so we can write the golden ratio differently:

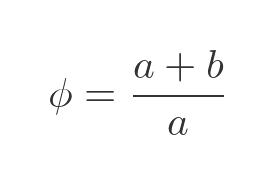
To find the value of ϕ, we need to somehow eliminate the unknown values a and b. We can use a simple trick of dividing the top and bottom of the fraction by b:

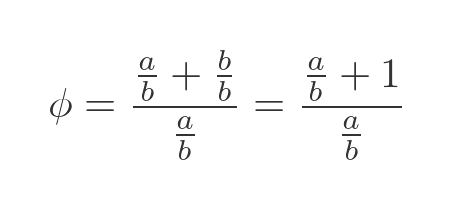
We can now use the fact the a/b is equal to ϕ to obtain an equation that depends only on ϕ:

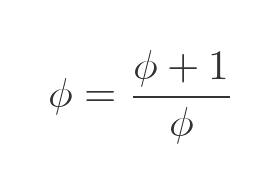
Multiplying both sides by ϕ, and bringing everything to the LHS gives us a quadratic equation:

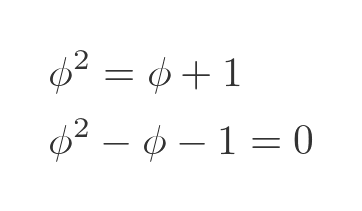
Applying the quadratic formula gives two potential solutions:

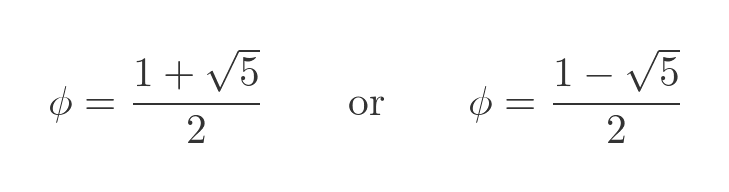
The second solution is a negative value, so we will eliminate it because, of course, the ratio of the sides of a rectangle is always a positive value. This gives us a value for ϕ:

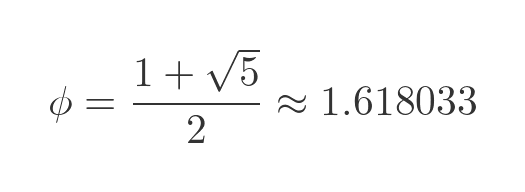
The golden ratio is irrational

One interesting point is that the golden ratio is an irrational value. We can see this by rearranging the formula above like this:

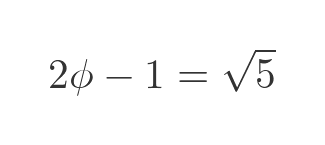
If ϕ was rational, then 2ϕ - 1 would also be rational. But since the square root of 5 is irrational, 2ϕ - 1 must be irrational. Therefore, ϕ must be irrational.

Origins of the golden ratio

The golden ratio crops up in various parts of geometry, and that is where it was first studied. Euclid's Elements describes is as:

A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser.

This is a more verbose way of expressing the formula relating a to b, given at the start of this article.

One particular example is in regular pentagons. The ratio between any diagonal (such as AD) and any side (such as AB) is the golden ratio:

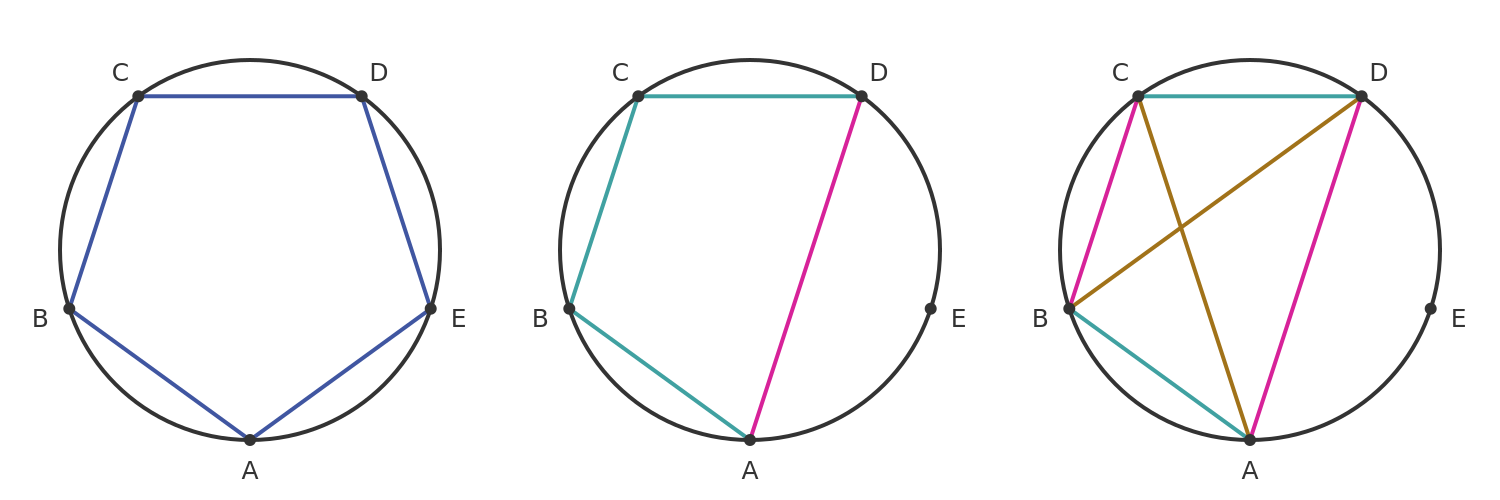
The LHS shows a regular pentagon. Any regular polygon is cyclic (it fits in a circle), as shown. The length of each side of the pentagon (AB etc) is b, and the length of any diagonal between two non-adjacent vertices (AD etc) we will call a.

If we ignore vertex E, we have a cyclic quadrilateral that is inscribed within the same circle. Notice that this quadrilateral has three sides of length b and one of length a. Ptolemy's Theorem applies to cyclic quadrilaterals, and states that:

If a quadrilateral is cyclic then the sum of the products of the lengths of the pairs of opposite sides is equal to the product of the lengths of its diagonals.

As a formula (the RHS of the image) this is:

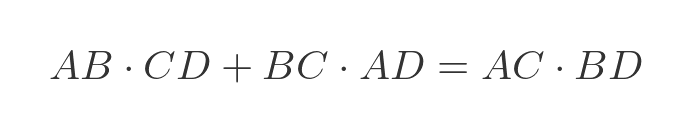
We know that AB, BC and CD are sides so have length b. Also, AC, BD and AD are diagonals with length a. So the previous equation becomes:

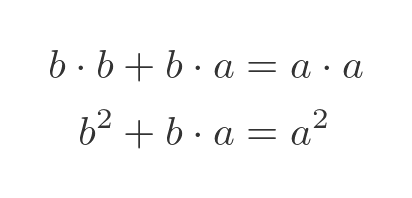
If we divide through by b squared and then simplify we get:

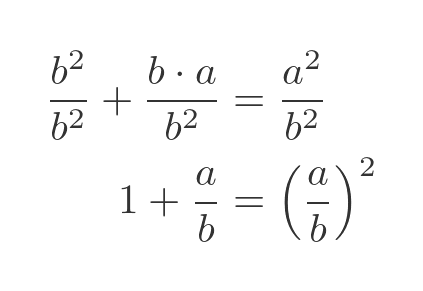
We are trying to find the ratio of a to b. Let's call this ratio r. We can replace a/b with r:

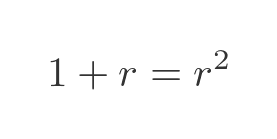
This is the same equation we saw earlier for ϕ, so this equation has the same solution. This proves that the ratio of a to b is in fact ϕ.

The inverse of ϕ

If we find the inverse of ϕ using a calculator, we get an interesting result:

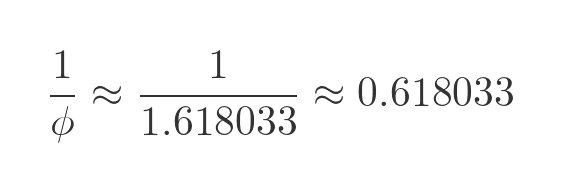
The inverse of ϕ has the same decimal part as ϕ itself! This unique property is easily explained using the earlier expression for ϕ:

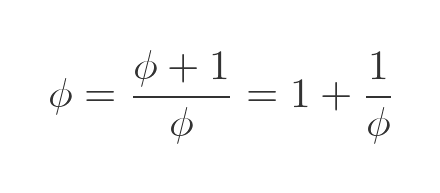
This can be rearranged to give:

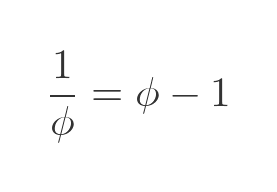
Of course, subtracting 1 from ϕ leaves the decimal part unchanged.

Powers of the golden ratio

The powers of ϕ follow a unique pattern. Let's start with a couple of obvious facts:

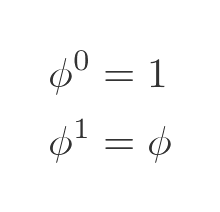
These follow because any non-zero number to the power 0 is 1, and to the power 1 is itself. We also have an expression for ϕ squared, from earlier:

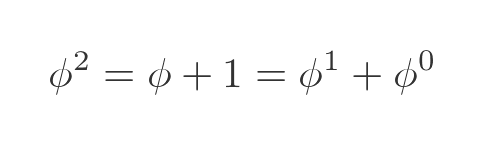
Here, ϕ and 1 are expressed explicitly as powers of ϕ. This makes it easier to see the pattern that is about to emerge.

Let's look at ϕ cubed. This, of course, is equal to ϕ times ϕ squared, and we already have an expression for ϕ squared. This allows us to write:

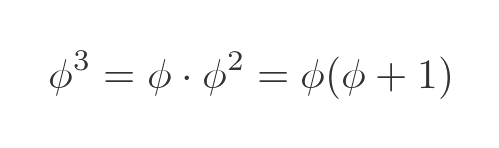
Multiplying out the brackets gives:

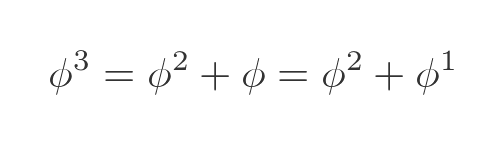
Repeating this for ϕ to the fourth power gives:

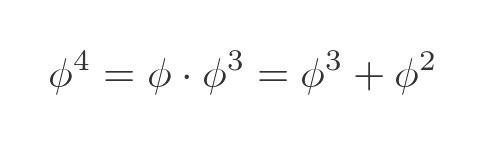
There is now a clear pattern:

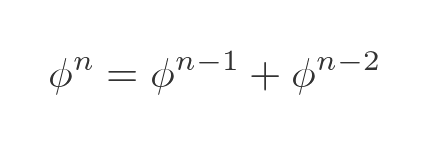
This is true for all n. It is easy to prove by induction, but we won't go through the proof here.

Powers as Fibonacci numbers

Recall that the Fibonacci are 0, 1, 1, 2, 3, 5, 8, 13... where each number in the sequence is the sum of the previous two numbers. In other words, the nth Fibonacci number (starting the numbering from 0) is:

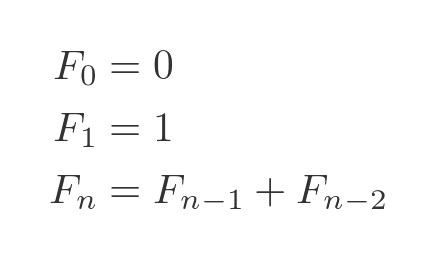
Now we can write the first power of ϕ in terms of Fibonacci numbers like this:

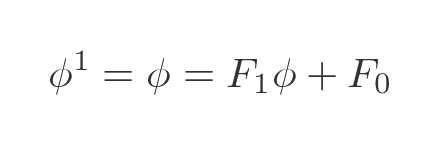
This relies on the fact that F0 is 0 and F1 is 1. It might seem a strange way of expressing it, but the reason will become clear soon. We can also write ϕ squared like this:

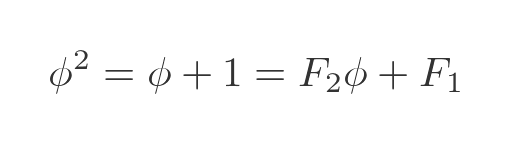
Again, this works because F1 and F2 are both equal to 1. Now let's look at ϕ cubed, using this equation from earlier:

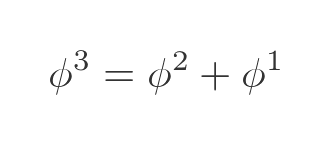
This time we can replace the two ϕ terms with the previous results involving Fibonacci numbers:

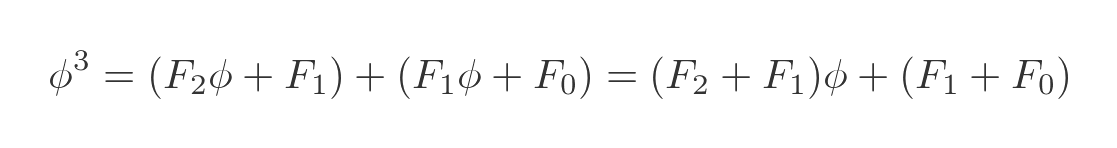
Now, from the definition of Fibonacci numbers, we know that F1 + F0 gives F2, and F2 + F1 gives F3, because each Fibonacci number is the sum of the previous two Fibonacci numbers. So we can write this as:

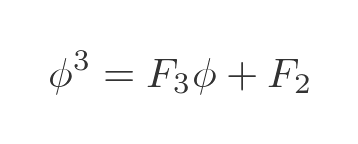
We can generalise this to find the nth power of ϕ. Again this can be proved by induction but we won't prove it here:

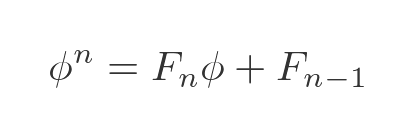
So the nth power of ϕ is equal to an integer multiple of ϕ plus another integer, where both integers are consecutive Fibonacci numbers.

The golden spiral

At the start of the article, we showed how we could convert a golden rectangle into a larger golden rectangle, simply by adding a square to it. We could, of course, do the same thing again to create an even larger golden rectangle. We could repeat this any number of times.

Here is what we get if we do this eight times. This shows the smallest rectangle and all the intermediate rectangles until we arrive at the largest rectangle. Each new rectangle formed by adding a square to the smaller rectangle, and the square is added to the side that causes a counterclockwise rotation:

If we draw a smooth curve through the corner of the square portion of each of the golden rectangles, we get a logarithmic spiral, shown in red.

Compare this with the Fibonacci spiral below. This looks very similar but it is subtly different. The rectangles are not golden rectangles. Instead, the first rectangle is made up of two squares, each of side length 1. The next rectangle adds a square of side 2, the next a square of side 3, then 5, 8, 13 and 21 - each side length is a Fibonacci number. This means that the rectangles is this shape are not quite similar. Each rectangle has the ratio of two consecutive Fibonacci numbers:

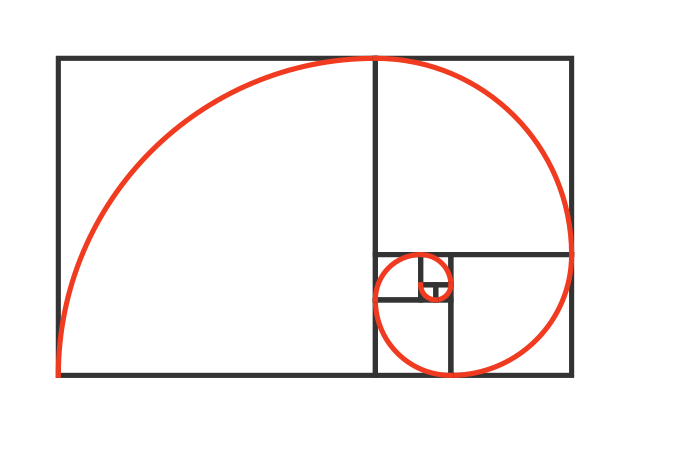
Why does this look so much like the golden spiral? Well, we get a clue if we divide the Fibonacci number n + 1 by the Fibonacci number n. For large n this ratio gets closer and closer to ϕ:

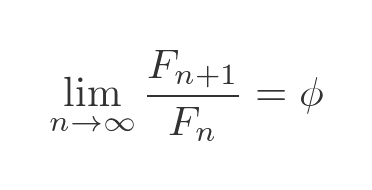
This means that, away from the centre, the two spirals are almost the same shape.

Summary

The golden ratio has fascinated mathematicians for more than two thousand years. This is in part because it is so accessible, requiring only basic algebra and geometry, and in part because it touches so many different branches of maths. In this article we looked at just a few of its interesting properties.

See also

• Factorials
• Prime factors of a number
• Lowest common multiple (LCM) of two numbers
• Greatest common divisor (GCD) of two numbers
• Trinary numbers
• Root 2 is irrational - proof by prime factors