Mathematical models in mechanics

In mechanics, we deal with real-world objects. In particular, we consider the effect forces acting on objects.

Using mechanics we can predict whether and system of objects will be stable, for example, whether a ladder against a wall will slip if someone climbs it. We can also predict the motion of objects, for example where a ball will land if you throw it in a particular way, or how long a pendulum will take to swing back and forth.

We make calculations by creating a mathematical model of the system we are trying to analyse. To simplify the calculations, we will often make assumptions about the system.

For example, if we were calculating the path of a ball that someone has thrown, we might decide to ignore the effects of air resistance. This will make the calculations a lot simpler but might make the result slightly less accurate. For a heavy ball, such as a cricket ball, the effect of air resistance is very small so the result would be very accurate. For a very light object, such as a balloon, then air resistance would be much more significant, and ignoring it would give a very inaccurate result.

In this section, we will look at some of the typical assumptions we make when modelling systems.

Characteristics of objects

We will often use certain terms to describe objects. In mathematics, these terms have specific meanings that are slightly different from their everyday use.

Light - We describe an object as light if it has such a low mass that it can be ignored. For example, if a weight is hanging on a string then the string might be so light that it doesn't need to be considered in the calculation. On the other hand, if the weight was hanging on a heavy chain, it would need to be considered.

Rigid - An object is described as rigid if it cannot bend, buckle, stretch, or change shape in any significant way. For example, a pencil or sheet of glass would normally be considered rigid, whereas a piece of string or a sheet of paper would not.

Rough/smooth surface - Rough surfaces exhibit friction. For example, if you tried to push a wooden crate across a concrete floor, it would take a lot of effort because of the friction, so the crate and the floor would be described as rough. With a smooth surface, the friction is negligible and can be ignored, for example, if you tried to push a wooden crate across an ice rink. A smooth surface means there will be no significant friction even if a rough object is moved across it.

Inextensible - Typically this is applied to strings. A string is inextensible if it will not stretch when pulled. Strings or chains are often inextensible. A length of elastic, or a spring, are examples of extensible objects. Notice that rigid objects are always inextensible because they cannot change shape in any way. However, not all inextensible objects are rigid. The term inelastic is sometimes used to mean the same thing.

Uniform - An object is uniform if its mass is evenly distributed over its volume, or in other words if it has uniform density. That will usually apply to any object that is entirely made of one material, such as a particular type of metal. If an object is uniform, then it can often be considered to be like a point object where all the mass is concentrated in one point, the centre of mass.

Types of object

Particle - A particle is an object that has mass but is so small that it can be modelled as if all the mass exists at a single point. Since the object is very small, we can ignore any rotation or air resistance. When we describe an object as being small, that is relative to the overall system that is being modelled. So, for example, if we were calculating the motions of the solar system, we might treat the Sun and the planets as points.

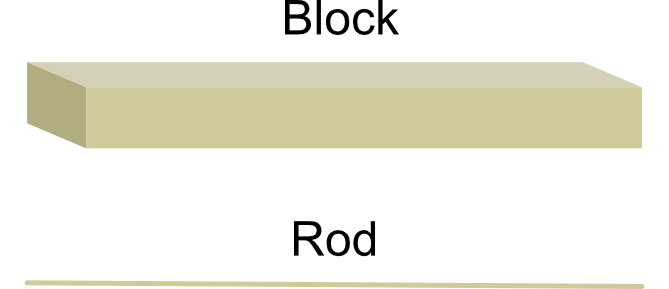
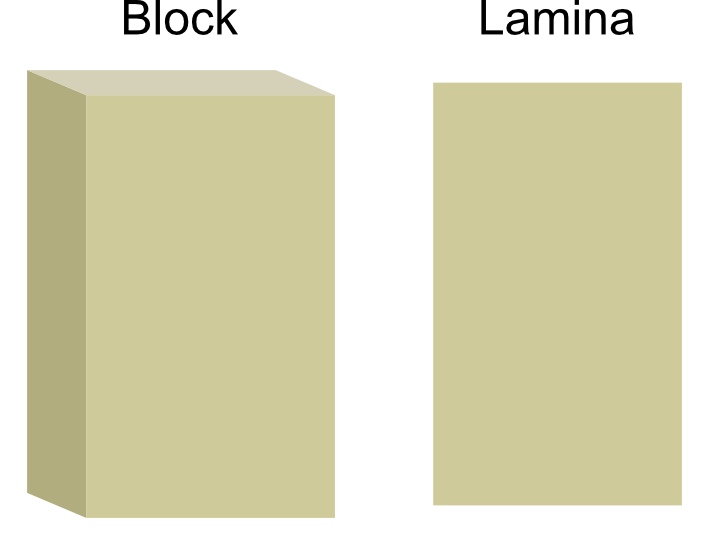
Rod - A rod is an object where the width and height are very small compared to the length. We can treat a rod as if it were a one-dimensional object, with zero width or height. If the rod is uniform, its mass is distributed evenly across its length, so its centre of mass is halfway along the rod. A rod is rigid.

Lamina - A lamina is an object where the thickness is very small compared to its width and height. We can treat a lamina as if it were a two-dimensional object, with zero thickness. If the lamina is uniform, its mass is distributed evenly so its centre of mass is at its geometric centre. A lamina may be rigid (such as a sheet of glass) or not (such as a sheet of paper).

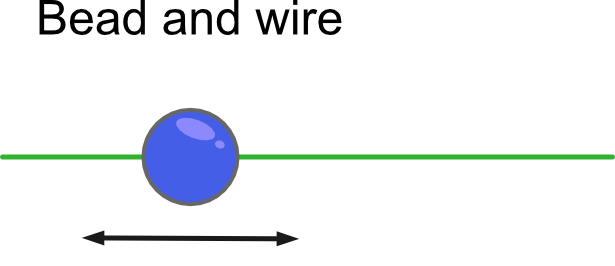
Wire - A wire is a specific type of rod, that can have beads threaded onto it. A wire can be either rough or smooth.

Bead - A bead is a specific type of particle that can be threaded onto a wire, and can move backwards and forwards along the wire. This effectively constrains the movement of the particle to one dimension. The bead will be subject to friction if the wire is rough

String - A string models a physical object such as a string, rope, or chain. It is one-dimensional, like a rod, but it is not rigid except when it is in tension. In other words, a string can pull another object but it can't push another object. A string may or may not be light, and it may or may not be inextensible.

Pulley - A pulley consists of a wheel that allows a string to move up and down. If pulley may or may not be light (it takes no effort to turn the wheel) and smooth (there is no friction) as the string moves.

Peg - This is a support that an object can either be suspended from or can rest on. Pegs are normally fixed (ie they never move) and are points, similar to particles. An example of a peg might be a nail in the wall, used to hang a picture.

Environment

There are several aspects of the environment that may need to be taken into account.

Air resistance - Air resistance is a type of friction acting by any object that moves in the atmosphere. As a form of friction, it operates against the movement of the object. It isn't limited to flying objects, of course. Cars, lorries, even cyclists experience air resistance. Air resistance is often ignored where it will have a negligible effect.

Wind - Wind is a force created by air moving relative to the object. It is in some ways similar to air resistance, but wind can affect stationary objects as well as moving objects. It can be difficult to take account of because it can fluctuate rapidly in strength and direction. It is usually ignored, but when designing things such as buildings or lorries it is often useful to calculate the maximum amount of wind the object can safely withstand.

Gravity - Any system on Earth is affected by gravity. The Earth's gravity, g, causes an acceleration of approximately 9.8 ms^-2. This varies slightly depending on where on the Earth it is measured, for various reasons, but the differences are less than 1%. The figure of 9.8 is generally used in all calculations.