Fractal dimension of self-similar fractals

In geometry, we often deal with 2-dimensional or 3-dimensional objects. Sometimes we look at 1-dimensional objects, and less often we might deal with objects that have four or more dimensions. In all cases, the number of dimensions is a natural number, that is an integer of one or greater.

Fractals don't behave quite like other shapes, in particular, they don't behave quite like normal 1, 2, or 3-dimensional shapes. It is useful to consider them to have non-integer dimensions.

In this article we will look at what this means, and why it is useful. For simplicity, we will only consider the case of self-similar fractals. The same ideas can be applied to other types of fractals, and even fractal-like natural objects such as coastlines, but that will be covered in a later article.

First, we will look at a useful way of thinking about normal dimensions that can be extended to fractal dimensions.

Measures

We will be looking at many different types of shapes, and discussing how big those shapes are. For 1-dimensional shapes we will be comparing their lengths, for 2-dimensional shapes we will be comparing their areas, and for 3-dimensional shapes we will be comparing their volumes.

For consistency, we will use the term measure, written as m, to describe how big a shape is, where measure can mean length, area, or volume, depending on the type of shape being discussed.

One way to think of this is to imagine the relative measure of two objects as being equal to their relative mass, assuming they are made out of the same material. 1-dimensional shapes might be made of a metal wire with the same thickness and density, 2-dimensional shapes are made from a metal plate, and 3-dimensional shapes are made of solid metal.

For fractals, we use the same model.

2-dimensions

Consider these two squares:

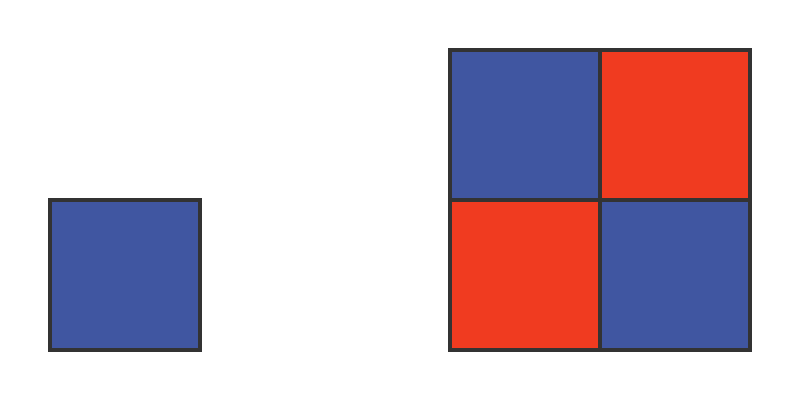
A square is a 2-dimensional shape, of course. The large square is the same shape as the small square (they are both squares, and all squares are similar shapes).

Since this is a 2-dimensional shape, its measure is area. We will define the smaller square as being of unit width and unit measure.

In this case, the large square linear dimension, s, is 2 (i.e., twice that of the small square). Its measure, m, will therefore be 4:

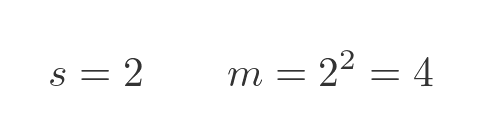
In general, for any value of s, the measure will be:

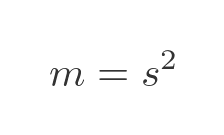
This is no surprise. When the linear size increases by a factor of s, the measure increases by a factor of s in both dimensions. The measure is s to the power 2 because the shape is 2-dimensional.

Other dimensions

Here are two cubes. The large cube is made up of eight copies of the smaller cube (shown slightly separated for illustration):

This time, the cube's linear dimension has increased by a factor of 2, and its measure has increased by a factor of 8. In general, when the linear dimension increases by a factor of s the measure increases by:

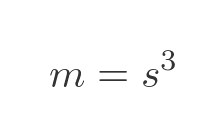
Again, since the cube has increased in size by a factor of s, this time in three directions, the measure increases by a factor of s to the power 3.

Finally, let's look at the 1-dimensional case:

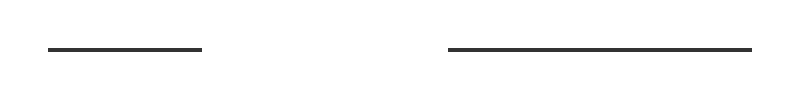
In this doubling the line length simply doubles its measure, so:

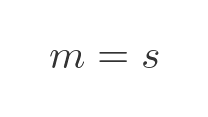
Sierpinski triangles

We will now move on to fractals, starting with the familiar Sierpinski triangle:

The Sierpinski triangle is a self-similar fractal. The main triangle is composed of three other triangles, where each of the smaller triangles is an exact copy of the original triangle (ie they are congruent). If we combine three of the triangles above, we create a larger triangle. Due to the self-similarity of Sierpinski triangles, the larger triangle is an exact (but scaled up) copy of the original triangle:

You might initially think that the Sierpinski triangle is a 2-dimensional shape - after all, it lives on the 2-dimensional plane. But a closer examination suggests that might not be true.

The small triangle above is the same size as the three parts of the large triangle. This tells us the big triangle has twice the linear dimensions of the small triangle (the base of the large triangle is formed from the bases of two of the small triangles).

But what is the measure of the large triangle? Well, it is made up of three of the small triangles. If we imagine that each of the small triangles is intricately cut from a metal plate, then the large triangle would weigh three times as much as the small triangle. So the measure is 3.

Something is wrong here. If the shape were 2-dimensional, then surely when the s is 2 we would expect m to be 4, not 3?

But wait, isn't m equal to 3 because we have left the middle triangle empty? Couldn't we do exactly the same thing with solid triangles? Like this:

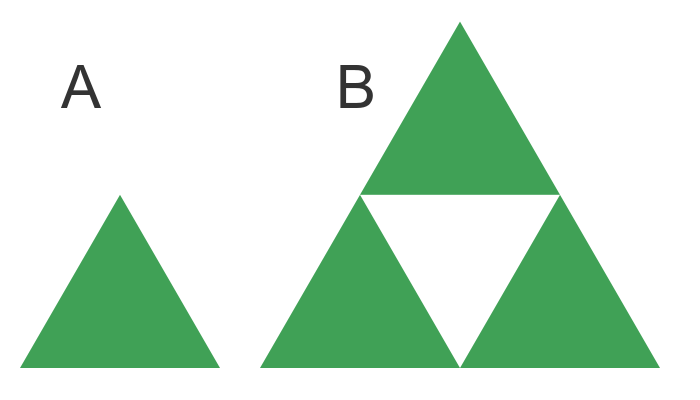
The problem here is that, when we miss out the middle triangle, the small triangle A and the large triangle B are no longer congruent. When we looked at dimensions earlier, we were looking at how m varies with s when we compare the same shape at different sizes. If we are allowed to change the shape, then we would be comparing a certain shape of a certain size with a different shape of a different size, which would tell us nothing.

We can't compare the solid triangle A with triangle B with a hole. To make the comparison valid we would need to cut a triangle hole A. But that still wouldn't be right, because now we would need to cut a hole in each of the three solid triangles in B. Then we would need to make the corresponding change in A, and so on.

We would carry on forever, cutting smaller and smaller triangles out of A and B in a never-ending quest to make them similar. And as we did that, the shapes would become more and more similar to a Sierpinski triangle. In fact, in the article on drawing Sierpinski triangles, one of the methods described is exactly that - to start with a solid triangle and recursively cut triangular holes.

For any 2-dimensional Euclidean shape, if we scale it by a factor s, its measure with increase by a factor s squared.

The reason a Sierpinski triangle doesn't follow this rule is because it is a fractal. That is the thing that allows its m to increase by 3 times when s doubles.

Extending the definition of dimension

So let's try to extend our definition of dimensions to cover fractal dimensions that might not be integers. We will start with the following formula, where D is the number of dimensions:

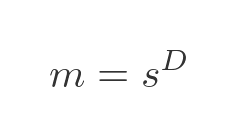
This just tells us what we already know. If we scale a shape up by s, its measure will be scaled up by s for 1-dimensional shapes, s squared for 2-dimensional shapes, or s cubed for 3-dimensional shapes. This assumes D is either 1, 2, or 3.

We can solve this for D, simple by taking the logarithm, base s, of both sides:

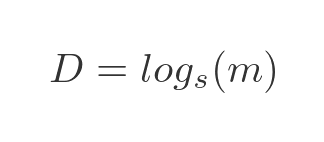
There is an alternative formula based on logarithms to some base a. It is derived from the standard formula for changing the base of a logarithm. This allows us to use, for example, natural logarithms for the calculation:

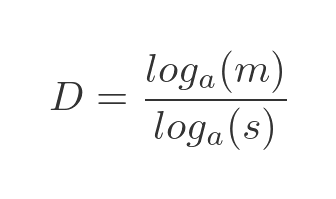
Using either of these formulas, we can calculate the fractal dimension based on the change in linear dimension and the corresponding change in measure.

Just as a check, let's plug in the numbers for a cube. When s is 2, m is 8, so we have (since 8 is 2 cubed):

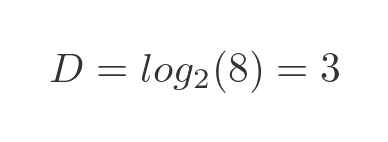
The fractal dimension of a Sierpinski triangle

For the Sierpinski triangle, we know that s is 2, and m is 3, so we can use the second formula (using natural logarithms) to find D:

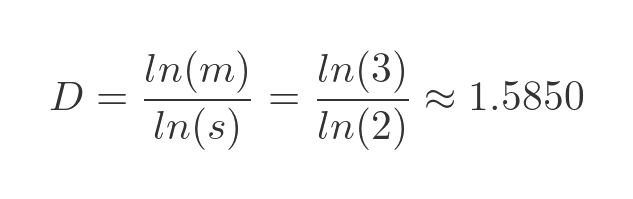
This tells us that a Sierpinski triangle is somewhere between being 2-dimensional and 1-dimensional.

Some other examples

Here is another well-known fractal, the Koch curve. As with the Sierpinski triangle, we show a small Koch curve together with a larger curve created from several copies of the smaller one. The two curves are identical apart from their size:

The curve is based on this shape:

If you look carefully you will see that the larger curve is made up of four copies of the small curve, arranged in that characteristic shape. This means that the measure m is 4. The triangular section of the basic shape forms an equilateral triangle. This means that the large shape is exactly three times the width of the small shape. So we have an s value of 3. The fractal dimension is, therefore:

Here is a variation of the Koch curve, called the quadratic Koch curve:

The curve is similar to the Koch curve, but is based on this shape:

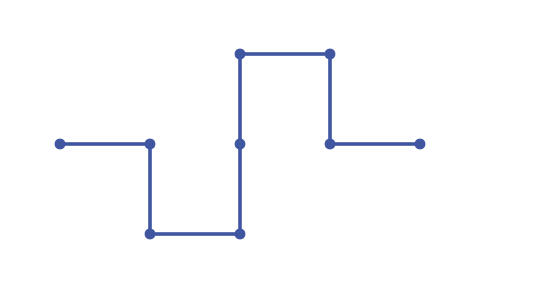
This time, all the angles in the base curve are right angles. There are eight line sections in the curve since the central vertical line is made up of two segments. The total figure is four times wider than one of the segments.

So this time the larger curve is made up of eight copies of the small curve, arranged in the base shape. This means that the measure m is 8. As we said earlier, the s value is 4. The fractal dimension is, therefore, exactly 1.5:

Fractal dimensions of a 3-dimensional Sierpinski triangle

We can create a 3-dimensional version of a Sierpinski triangle. We start with a regular tetrahedron (a 3-dimensional shape made of four identical equilateral triangles):

The shape above is drawn as four smaller tetrahedrons (in blue) plus an extra red shape in the middle. This red shape is actually a regular octahedron, where each face of the octahedron is identical to one of the blue triangles. If we remove this octahedron, we are left with just the four small tetrahedrons:

We can remove a similar octahedron from each of the small blue tetrahedrons, which will leave 16 even smaller tetrahedrons. Repeating this an infinite number of times results in a Sierpienski tetrahedron, like this:

What is the fractal dimension of this shape? Well, we can take four tetrahedrons to create a larger, identical tetrahedron. And when we do that, the linear dimension of the shape increases by two. So m is 4 and s is 2.

We don't need to calculate this dimension, we already know it. If doubling s increases m by a factor of 4, then the dimensionality of the shape is, of course, 2. So the tetrahedron above is actually 2-dimensional!