How carbon dating works

We have all heard of carbon dating, of course. In this article, we will take a look at how it works.

This article is in part inspired by an article I read recently claiming that carbon dating proves that diamonds mined from deep underground are in fact only a few thousand years old! We will see why that claim is incorrect later in the article.

What is carbon dating

All living things contain carbon, and most of that carbon comes from C02 in the atmosphere. Plants absorb CO2 directly from the atmosphere and convert it to carbohydrates via photosynthesis. Animals get their carbon either by eating plants or by eating other animals that (ultimately) got their carbon by eating plants. One way or another, the vast majority of carbon in living things comes from the atmosphere.

The atmosphere contains three main isotopes of carbon which we will discuss in more detail later. These are C12 which makes up about 99% of the carbon in the atmosphere, C13 which makes up about 1%, and C14 which is about one part per trillion. Since the carbon in a living organism comes from atmospheric carbon, the proportion of the three isotopes in land-based living organisms will match the proportions in the atmosphere (marine life forms are slightly different).

C12 and C13 are both stable isotopes, but C14 is unstable. It decays, with a half-life of about 5,700 years. However, new C14 is continuously being created in the atmosphere as described later.

While an organism is alive, it will be continuously replenishing its carbon with fresh carbon from the atmosphere, so its proportion of C14 will be roughly equal to that of the atmosphere. But as soon as it dies, it will no longer be replacing its carbon. The C14 it contains will gradually decay over hundreds and thousands of years. We can estimate its age from the proportion of remaining C14.

Limitations of the technique

Carbon dating only works with organic material. If the material was never alive, it is unlikely that most of the carbon it contains came from the atmosphere at a specific time.

Also, since the half-life of C14 is 5,700 years, it will not work with extremely old samples. After 57,000 years, that is ten half-lives, only about 0.1% of the original C14 will be left. It is difficult to measure this amount accurately, as other sources of tiny amounts of C14 could affect things.

That is basically why we can't use carbon dating on diamonds. Diamonds are far too old, and they were never alive in the first place. But if diamonds have been deep underground for millions of years, why do they have any C14 at all? To answer that we need to know a bit more about C14.

What exactly is C14?

Atoms, of course, are made of three types of particles - protons, electrons and neutrons. The number of protons, the atomic number, determines what the element is. Carbon has 6 protons, and that is what makes it carbon. The number of electrons always equals the number of protons, because electrons have a negative charge and protons have a positive charge, and an atom must have zero total charge.

Atoms usually have approximately the same number of neutrons as protons, but since neutrons have no charge, an atom doesn't need to have exactly the same number of neutrons and protons.

Stable forms of carbon can have either 6 to 7 neutrons. We call these the stable isotopes of carbon - they are both carbon because both have 6 protons, and that means they are chemically almost identical. But they are not completely identical because they have different numbers of neutrons. We name an isotope after the total number of protons and neutrons. The variant of carbon with 6 neutrons is called C12 (6 protons plus 6 neutrons) while the variant with 7 neutrons is C13.

A combination of 6 protons and 8 neutrons makes C14. This is chemically very similar to C12, but it is quite different in another way - it is unstable. It might be around for thousands of years, but at some point, it will decay. Another way to express this is to say it is radioactive. Every C14 atom will eventually decay, emitting a high-energy particle - that is, radiation.

The isotopes of carbon are shown here, with blue circles to represent neutrons and red circles to represent protons. The chemical symbol C has two numbers. The lower number is the number of protons (the atomic number, always 6 for carbon) and the upper number is the total number of protons and neutrons (the atomic mass number).

There are other known isotopes of carbon, from carbon 8 through to carbon 22. Only C12, C13 and C14 are found in the atmosphere. In part, this is due to the other isotopes having much shorter half-lives, measured in minutes or seconds rather than thousands of years.

How is C14 formed in the atmosphere?

The upper atmosphere is continuously bombarded with cosmic rays from the Sun, from other stars in our galaxy, and from other galaxies. They aren't really rays, that name was given before we understood what they were. They are actually highly energetic particles (atomic nuclei or individual sub-atomic particles) travelling at close to the speed of light. When they collide with atoms in the atmosphere, they break into various smaller high-energy particles, including neutrons. Those smaller high-energy particles will sometimes collide with other atoms, creating yet more particles.

This creates all sorts of particles, but are only interested in one particular case. It is the relatively common secondary event of a high-energy neutron hitting a nitrogen atom - the atmosphere is 80% nitrogen, after all. The neutron sometimes knocks a proton out of the nucleus of the nitrogen atom and takes its place.

Nitrogen has 7 protons and 7 neutrons. If a neutron replaces one of the protons, it leaves 6 protons and 8 neutrons - a C14 atom. This isn't the only way C14 can be formed, but it is the most common. This event is illustrated below:

How does C14 decay

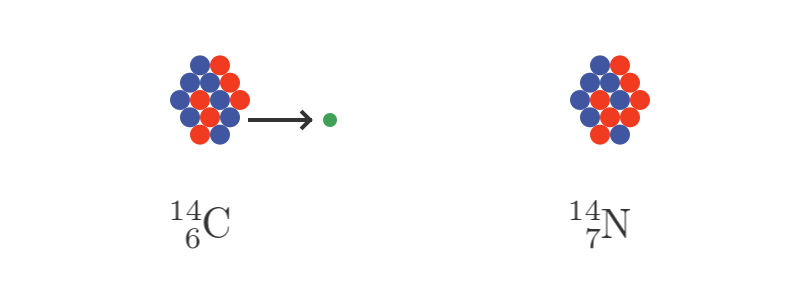
The C14 nucleus is unstable. Usually, one of its neutrons decays into a proton. When this happens it emits a high energy electron. We call this beta radiation.

Since C14 has 6 protons and 8 neutrons, if one of the neutrons decays into a proton, we end up with 7 protons and 7 neutrons. That is a nitrogen atom, so we are back where we started:

Doesn't carbon dating assume the C14 ratio has always been the same?

We can't assume that the C14 ratio has always been the same, in fact we know that it has changed over time.

The most significant factor, historically, has been variation in the cosmic rays reaching the atmosphere from the Sun. This is affected by both solar activity and variations in the Earth's magnetic field.

A lot of work has been done to correct for this effect. This mainly consists of measuring artefacts of known age. Tree rings have been studied extensively for this purpose. The C14 in each ring comes mainly from that year's growth, so a tree sample can yield the history of annual atmospheric C14 levels over its entire life. Trees from overlapping periods can be calibrated against each other, and based on that we have accurate calibration data going back 8000 years.

There is also a slight difference between the northern and southern hemispheres. This occurs because the southern hemisphere has a greater ocean-to-land area, which can affect atmospheric CO2 levels. And since the northern and southern hemispheres have largely independent atmospheric circulation systems, the differences can persist for some time. This leads to a time difference of about 40 years between the two hemispheres.

Carbon dating marine life requires special care. The sea absorbs carbon from the atmosphere, but the circulation of that carbon is far slower than in the atmosphere. This leads to even longer time differences between the oceans and the atmosphere, and also quite large differences for different regions. This can lead to errors of hundreds of year when dating marine samples if it is not corrected for.

Finally, nuclear weapons testing, starting in the 1940s, had a significant effect on the amount of C14 in the atmosphere from that date forward.

So why do diamonds contain C14?

This still doesn't explain why diamonds, which have been underground for millions of years, contain C14?

Levels typically reported in diamonds are very low. They are at the limits of what can be measured, and indicate an "age" of 50,000 years plus. The age, of course, would only apply if diamonds had once been alive, which of course they were not.

Such low values could easily come from measurement errors or accidental contamination.

But in some cases, it might also be due to other sources of radiation, particularly uranium. Uranium emits alpha radiation, which is essentially high-velocity helium nuclei (a cluster of two protons and two neutrons). These particles can collide with other atoms, creating various other free particles including high-energy individual neutrons. Diamonds often contain impurities such as nitrogen atoms trapped within the crystal structure. Neutrons colliding with these nitrogen atoms will sometimes create C14 atoms.

And, of course, when the C14 eventually decays it turns back into nitrogen. So while ever the uranium remains radioactive, the tiny amount of C14 in the diamonds will be continually replenished, just like the C14 in the atmosphere. So diamonds that are millions of years old can contain traces of C14.

See also

• What is nothing? Kuhn's nine levels of nothing