100 prisoners problem

The 100 prisoners problem is a mathematical puzzle that seems impossible, but it has a solution. And the solution only requires a bit of simple logic. Yet it still seems counterintuitive even when you know the answer!

The problem

A prison holds 100 prisoners, each with a unique prisoner number from 1 to 100.

One day the warder decides to torment the prisoners by offering them a chance of freedom. But with the odds stacked so they have no chance of winning.

He places 100 boxes, numbered 1 to 100, in a room. He then takes 100 cards, again numbered 1 to 100. He places a card in each numbered box, completely randomly. Here, we can see the contents of the boxes, but the prisoners cannot until they open each box:

The prisoners are allowed into the room, one at a time, tasked with finding their own number. They are allowed to look in a maximum of 50 boxes to try to find their number.

When they are finished, they must leave the room exactly as they found it, and they are not allowed to communicate with the other prisoners who have yet to enter the room.

The warder promises that if every single prisoner finds their own number, they will all be released. But if any prisoner fails to find their number, then none of them will be released.

What are the odds?

There are 100 boxes, and each prisoner is only allowed to open 50 boxes. When a prisoner opens 50 boxes at random, then the chance of them finding their own number is 50/100, which is exactly one-half.

What are the chances that all 100 prisoners will find their own number? Well, each prisoner searching for their number is an independent event (it is not affected by the previous prisoners' searches because they can't pass information to each other). To find the probability of multiple independent tries being successful, we multiply the individual probabilities together. Since each probability is a half, we must multiply a hundred halves together:

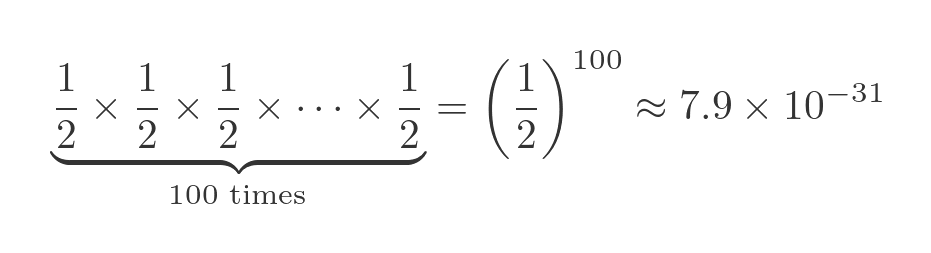
The probability of all 100 prisoners finding their numbers is very, very small (0.00000000000000000000000000000079). It is the equivalent of throwing a fair coin 100 times and getting heads every single time.

Put another way, it would be like walking up to a complete stranger in the street and guessing the full 16-digit numbers of two credit cards in their wallet.

It isn't going to happen!

But there is a simple strategy to reduce these astronomical odds to about 30%. Which isn't perfect but it gives the prisoners a reasonable shot at freedom.

The winning strategy

So what is this mysterious, odds-defying strategy? It is surprisingly simple.

Each prisoner opens the box corresponding to their own number and looks at the card inside. If that card has their number, they win. If not, they open the box corresponding to the new number. They keep going until they either find their number, or they have opened 50 boxes.

For example, let's see what happens to prisoner 14. They start by opening box 14 (because they are prisoner 14). This box contains card 51 (see for yourself in the boxes image above).

So they open box 51, which contains card 42. Then they open box 42 which contains card 69. Box 69 contains 28. Box 28 contains 77. Box 77 contains their card, number 14. They've found their number!

That's great, but it is no big surprise. If they had opened 50 boxes at random they might easily have found their number - approximately half the prisoners would, just by pure chance.

The question is, how can this strategy help the other half of the prisoners who we might expect not to find their number? How can going through the boxes in a particular order make such a massive difference to their chances, when the boxes themselves have been filled in a random order? It doesn't seem to make any sense.

Some facts about the search order

To understand the benefits of this way of searching, we need to understand some facts about how it works. These facts are all fairly obvious after you have seen them, and they can be proved using basic logic.

Before we get on to that, let's try a few more examples. But this time we will use 10 prisoners, boxes, and cards. The logic is still the same, but the examples are simpler. First, let's imagine the cards were distributed amongst the boxes like this:

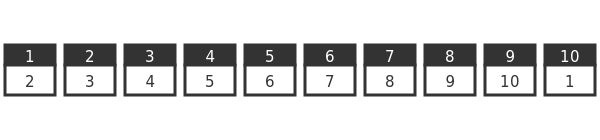
Let's assume prisoner 1 goes in first (although it doesn't affect the final result who goes first). They will open box 1, of course. This contains the number 2, so they will open box 2 next. If you notice, each box contains the next number, so they will go on to open boxes 3, 4, and so on, right up to box 10. Box 10 contains the number 1, so they finally find their number. This is shown here:

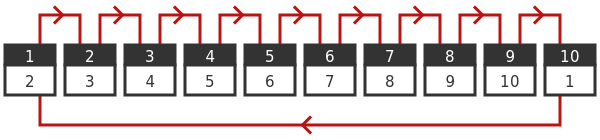
Notice that if we keep going for long enough we end up back where we started. We call this a loop, and it will be very important later. Notice also that even if we started with a different box, we would still end up in the same loop. For example, if we started with box 9, that would take us to box 10. And box 10 would take us to box 1, which is where the previous loop started.

Now let's look at a slightly different arrangement:

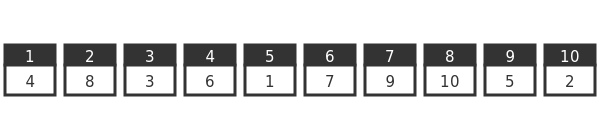
Again we will assume prisoner 1 goes first and opens box 1. Box 1 contains card 4. Box 4 contains card 6. 6 contains 7, 7 contains 9, 9 contains 5 and 5 contains 1:

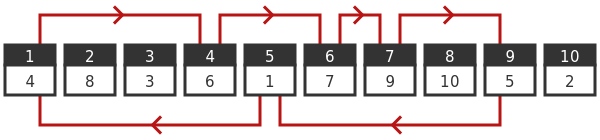
So once again we have a loop, but notice it doesn't contain every box. For example, box 2 isn't included in the loop. So what happens when prisoner 2 enters the room? They will start from box 2, of course:

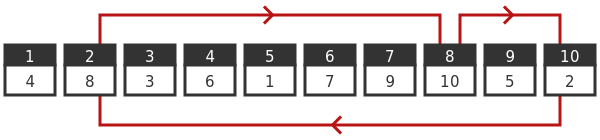
This time box 2 contains card 8, 8 contains 10, and box 10 takes us back to box 2. This is still a loop, but it is a different loop. As it happens, this loop only contains three boxes.

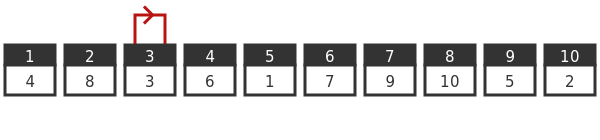
At this point, you will be wondering about box 3, the only box that hasn't been opened yet. Here it is. Prisoner 3 will be in luck, they will find their card the first time. Card 3 is in box 3:

So here are some observations, as yet unproven:

1 - It appears that every box is part of a loop.

2 - If we start with box n, we will always eventually find card n.

3 - Card n will always be in the last box we try, just before we loop back.

Finally, the most important one for us:

4 - If a prisoner starts at the box with their number, the number of tries they need to find their number will be exactly equal to the length of the loop they are in.

Proving these facts

Although the facts above might not be immediately obvious, it isn't difficult to prove that they are true.

1 - Every box is part of a loop. We can prove this by contradiction - we will assume that one of the boxes is not part of a loop, and show that this would lead to an impossible situation.

Let's assume that box n is not part of a loop. This means that, if we start from box n, no matter how many boxes we open, we will never encounter a box that contains card n.

But we also know that each box contains a unique card number. So each card must take us to a box that we haven't previously opened.

This means that we should be able to open as many boxes as we like, and each time we open a box it will contain the number of a new box that we haven't opened yet. And we will be able to keep doing that forever, never arriving back at box n.

But there are only a finite number of boxes, so it is impossible to keep opening new boxes forever. That is a contradiction.

This contradiction can only be resolved if our original box n is part of a loop so that within a finite number of tries we will be back where we started. And since n is the number of some arbitrary box, it follows that every box must be part of a loop.

2 - If we start with box n, we will always eventually find card n.

This follows from the previous proof that every box n is part of a loop. Since the loop will eventually bring us back to box n, it follows that one of the boxes in the loop must contain card n.

3 - Card n will always be in the last box of the loop.

When we reach a box containing card n, the next box will be box n, which is where we started from. This means that we will restart the loop immediately after encountering card n. So it follows that the last box in the loop must contain card n.

4 - If a prisoner starts at the box with their number, the number of tries they need to find their number will be exactly equal to the length of the loop they are in.

This follows from the previous statement, 3. The prisoner will always find their number in the last box of the loop, and therefore the number of tries required will always be equal to the length of the loop.

What this tells us

Returning to the 100-prisoner scenario, we now know that (by following the strategy) every prisoner will find their card is a number of tries that is equal to the length of the loop they are in. So if every loop has length 50 or less, they will all find their numbers:

All the prisoners will find their number in the first 50 boxes if, and only if, there is no loop with lengths greater than 50.

Notice that this statement is about the condition for ALL the prisoners to succeed. If we can calculate the probability that there will be no loops longer than 50, then that will be the probability that all the prisoners get released.

This is very different to the naive strategy of picking boxes at random. In that case, the probability that any individual prisoner would find their number is 50%. But it is impossibly unlikely that all 100 prisoners would find their number.

Calculating the probability

So what is the probability that all the loops will have a length of 50 or less?

Well, it turns out that it is a lot easier to calculate the probability that there will be a loop of 51 or more. That is because, with 100 prisoners:

• There can be multiple loops of 50 or less, for example, there could be one, two or three loops of length 30.
• There can only be one loop of 51 or more.

What is even nicer, as we will see in a moment, is that the probability of there being a loop of 51 turns out to be 1/51. And the probability of a loop of 52 is 1/52. And so on, right up to 100.

And since only one of those situations is possible, the probability of there being a run of 51 or greater is a simple sum of the individual probabilities:

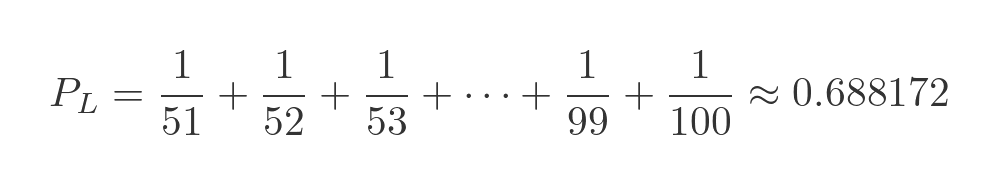
This, of course, is the probability that the prisoners will lose the challenge. The probability that they will win is therefore:

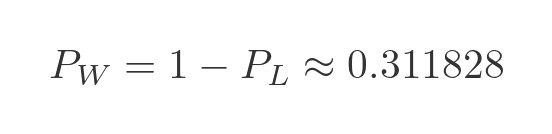
They can improve their odds from virtually zero to better than 30%, simply by searching the random boxes in a different order!

Calculation details

We will finish off by looking at how the previous result is derived - that the probability of a loop of length n existing is 1/n (only for loops of 51 or more, as explained above).

For this calculation, we will look at permutations of the numbers 1 to 100. We are only concerned with the numbers on the cards themselves, not which boxes they are placed in. For example, one possible arrangement of the numbers might be that the numbers 1 to 60 form a loop (with the numbers in that order), and the numbers 61 to 100 are not part of that loop.

We don't need to specify which boxes each card is placed in. To form the loop, box 1 must contain card 2, box 2 must contain card 3, etc, and box 60 must contain card 1. The remaining 40 cards are not part of the loop so we don't care how they are arranged.

So to calculate the probability that there will be a loop of 60, we need to know:

• How many possible ways there are to arrange the numbers 1 to 100?
• How many possible ways there are to arrange the numbers 1 to 100 such that there is a loop with a length of exactly 60?

The probability of a loop of 60 is then the second number divided by the first.

How many different ways are there to arrange the numbers 1 to 100? This is the number of permutations of the numbers. The number of permutations of n unique items is n factorial, so in our case there are 100! different ways to place the numbers in the boxes.

How many ways are there to arrange the numbers 1 to 100 so that they contain a loop of 60? If we were choosing to make a loop, we could imagine doing it in two steps. First, we might decide which 60 numbers should be included in the loop, Then we might decide how to order those numbers in the loop.

The number of ways to select 60 items from 100 is a standard result, called n choose r. In our case we are looking for 100 choose 60, which is:

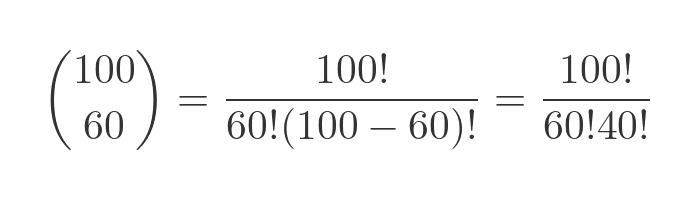
This just tells us the total number of ways of choosing 60 elements out of 100 unique elements. The second stage is to decide how to order those elements. There are 60 elements in the loop, so the total number of ways to arrange those elements is 60!. There are also 40 elements that are not in the loop, so there are 40! ways of arranging those elements.

But that isn't quite true. Earlier we gave the example where the loop was the number 1 to 60 in order. We said that box 1 must contain card 2, box 2 must contain card 3, etc.

But what about a different loop 2, 3, 4 ... 59, 60, 1? This is the same loop but rotated round by one place (the number 1 has been moved from the start to the end). So again box 2 contains card 3. And box 1 contains card 2 (to loop from the end of the sequence back to the start). In fact, these two loops will both result in exactly the same cards being placed in the first 60 boxes. They aren't really different loops at all.

The loop 3, 4, 5 ... 60, 1, 2 will be the same. There will be 60 different loops that result in the same cards being placed in those boxes. And this will be true for every other unique group of 60 numbers. So the total number of unique ways to arrange the elements will be 60! divided by 60.

For the 40 elements that are not part of the loop, there is no requirement for them to be connected in any particular way, so there are still 40! possible arrangements.

So the total number of unique arrangements that create a loop of 60 is given by the total number of ways to choose 60 elements, multiplied by the number of unique ways to arrange those 60 elements, multiplied by the number of ways to arrange the remaining 40 elements, That is, 100 choose 60, multiplied by 60!/60, multiplied by 40!:

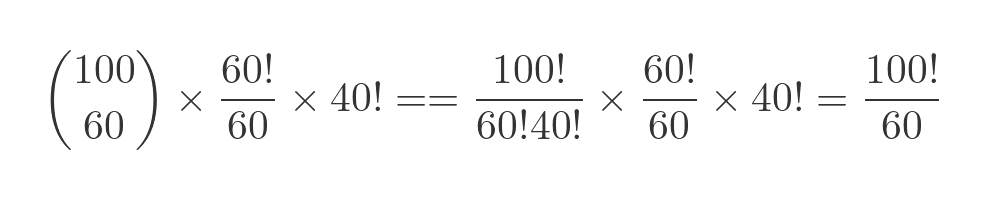
This is the number of unique arrangements that create a loop of 60. To calculate the probability we need to divide by the number of possible arrangements, which is 100!:

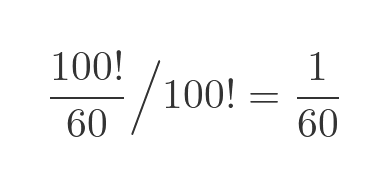
We have calculated this using an example loop size of 60. If we repeated the above for a loop size of n, we would obtain the probability 1/n that we used earlier.

See also

• Factors of a prime squared minus 1