Pythagorean triples

Pythagoras' theorem says that, for a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Here is an illustration:

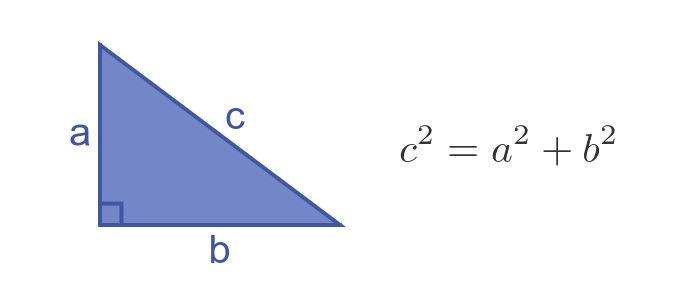
A special case of this rule is when the lengths of all three sides are integers. In those cases, we call the three lengths Pythagorean triples. They are also sometimes called Pythagorean triads.

Pythagorean triples

The most famous example of a Pythagorean triple is the (3, 4, 5) triangle:

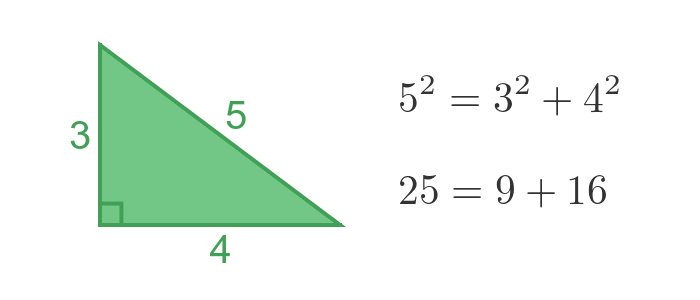
In this case, the hypotenuse has length 5, and the other two sides have length 3 and 4. 3 squared is 9, 4 squared is 16, which adds up to 25. And, of course, 5 squared is also equal to 25.

Another example is the (5, 12, 13) triangle:

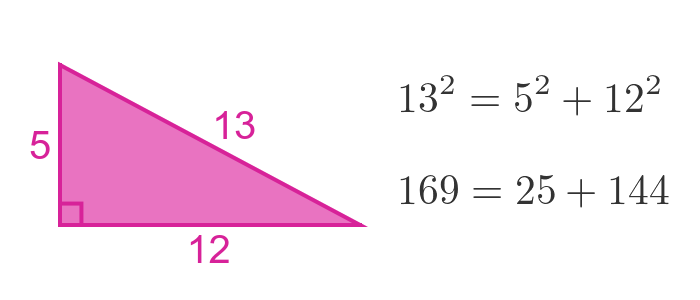
This time, 5 squared is 25, and 12 squared is 144, which adds up to 169, which is equal to 13 squared.

Pythagorean triples are a special case. Most right-angled triangles don't form Pythagorean triples, for example:

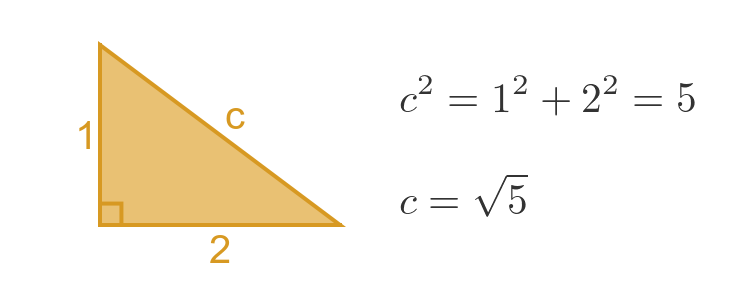
This triangle is not a Pythagorean triple because side c is not an integer.

Primary triples

The (3, 4, 5) triangle is called a primary Pythagorean triple because the numbers 3, 4 and 5 have no common factors.

If we multiply the length of each side by 2, we get a (6, 8, 10) triangle:

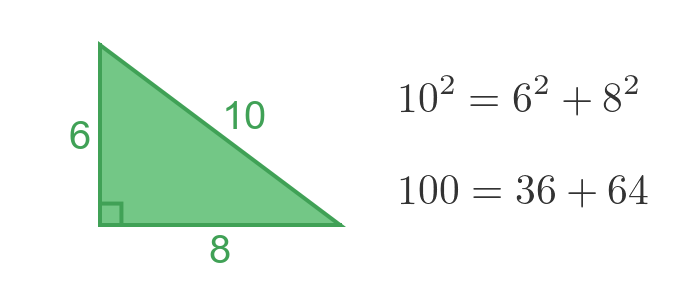
This triangle is similar to the (3, 4, 5) triangle because all the sides have been scaled proportionally. So (6, 8, 10) is a Pythagorean triple, but it isn't primary because the numbers all gave a common factor of two.

We can multiply by three to create a (9, 12, 15) triangle, or by four to create a (12, 16, 20) triangle, and so on.

The (5, 12, 13) triangle we looked at previously is also a primary Pythagorean triple, because those three numbers have no common factors. We can create further non, primary triples by multiplying by two (10, 24, 26), three (15, 36, 39), etc.

Primary triples are sometimes called reduced triples.

Odd/even properties of Pythagorean triples

If a, b and c form a Pythagorean triple, then one of the following is true:

• Either a, b and c are all even numbers.
• Or exactly one of a, b or c is even, the other two are odd.

Why is this true? Well, we must start by looking at a squared and b squared. They can each be either odd or even. We also know that c squared is the sum of these two values. We can create a table that shows all the possibilities:

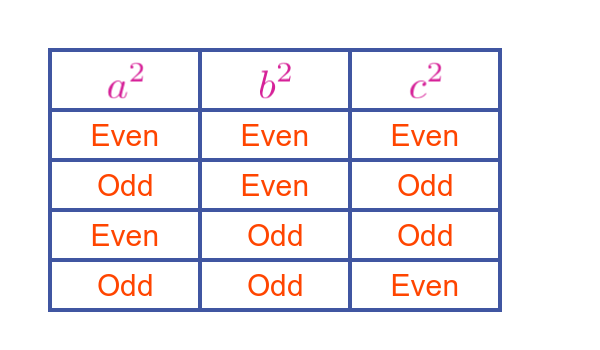
We can work out whether c squared is odd or even based on the other two values. If we add two even numbers the result is even. If we add an odd and even number, the result is odd. If we add two odd numbers, the result is even.

The table tells us that, for the three squares, they must either all be even, or two must be odd and the other one even.

But we also know that if x is even then x squared must be even, because two even numbers multiplied together is even. And also if x is odd then x squared must be odd because two odd numbers multiplied together is odd.

So we can create a new table showing the odd and even values of a, b and c. This table will be exactly the same as the squares table:

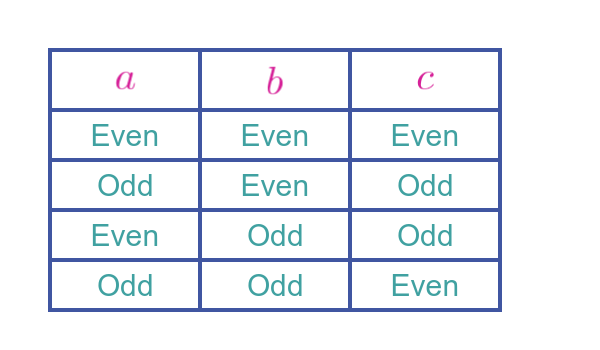
This proves the result above.

Generating Pythagorean triples using Euclid's formula

Euclid's formula allows us to reliably create Pythagorean triples based on a simple algorithm.

We first choose any two positive integers, m and n, with the condition that m is greater than n.

We can then calculate a, b and c using the following formulas:

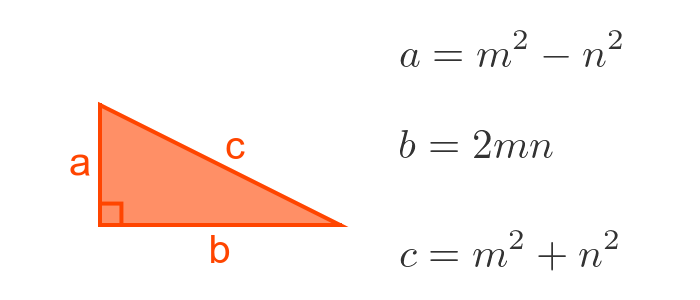
For any values m and n that meet the condition above, the three values a, b and c will always form a Pythagorean triple.

For example, if we choose m = 2 and n = 1 we get the famous (3, 4, 5) triangle:

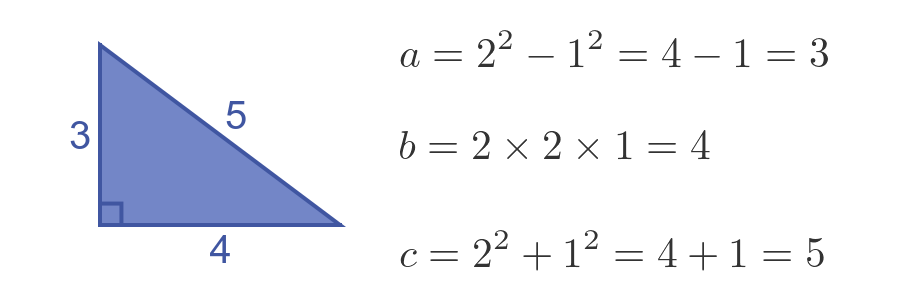
If you repeat the calculation with m = 3 and n = 2 we get a (5, 12, 13) triangle.

This formula will always create a Pythagorean triple, but:

• It doesn't create the triples in any particular order.
• Sometimes a will be bigger than b, and sometimes b will be bigger than a.
• It doesn't create every possible Pythagorean triple (but it does create all the primary triples).

Are there an infinite number of Pythagorean triples?

There are an infinite number of Pythagorean triples, and this is quite easy to prove.

Consider the triple (3, 4, 5).

We can create another triple by multiplying each value by 2:

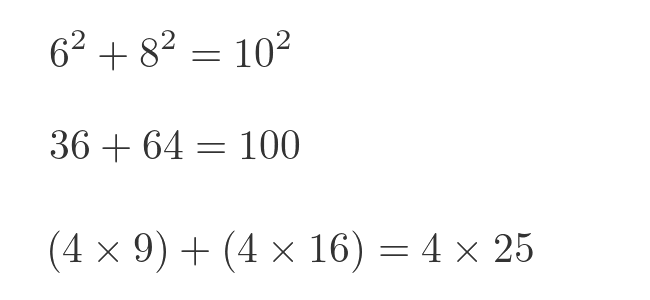
The triple (6, 8, 10) is still a Pythagorean triple. This is because multiplying each term by 2 is equivalent to multiplying each squared term by 4 (ie 2 squared) so the two sides are still equal.

We can repeat this multiplying each value by 3:

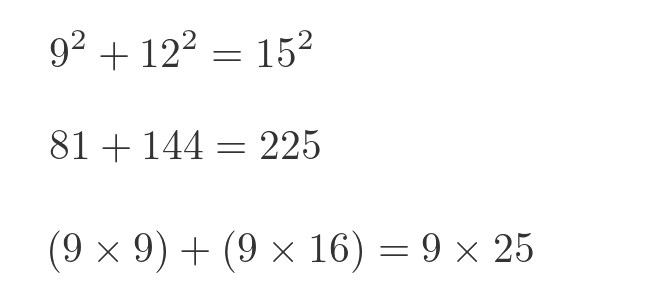
The triple (9, 12, 15) is also a Pythagorean triple. Multiplying each term by 3 is equivalent to multiplying each squared term by 9 (ie 3 squared).

If we multiply each term by any positive integer n, it creates a new Pythagorean triple:

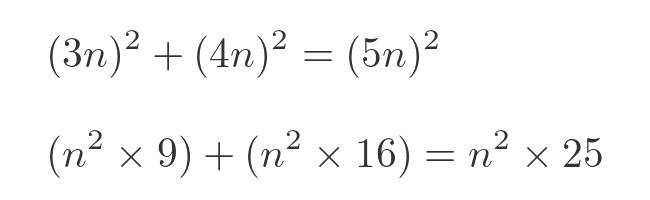
Since there are an infinite number of different values for the integer n, this creates an infinite number of different Pythagorean triples based on the (3, 4, 5) triple. So there are infinitely many Pythagorean triples.

Of course, this proof has ignored other triples. There are also infinitely many Pythagorean triples based on the (5, 12, 13) triple, and so on. But using the (3, 4, 5) triple alone is sufficient to prove that there are infinitely many triples.

Are there an infinite number of primary Pythagorean triples?

The proof above might seem unsatisfying, or even a bit of a cheat, because we have just taken one triple and multiplied by an infinite number of different values n. All the triangles produced by this method are similar triangles.

Perhaps a more interesting question is whether there are an infinite number of primary triples. Well yes, there are, and we will prove it next.

We will do this by looking at the set of primary triples that follow this pattern:

• (3, 4, 5)
• (5, 12, 13)
• (7, 24, 25)
• (9, 40, 41)

These triangles all follow the same pattern:

• The shortest side, a is an odd number.
• The hypotenuse c is one greater than the other side b.

There are examples above for a of 3, 5, 7, and 9. If this pattern carries on for every odd integer, that will create an infinite number of primary triples, proving our result.

Since we know that c = b + 1 we can write Pythagoras' theorem like this:

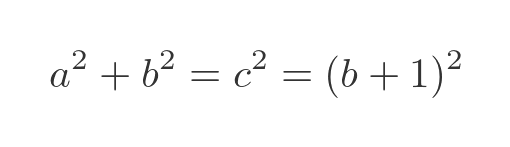
Expanding (b + 1) squared gives:

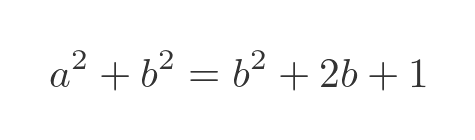
Subtracting b squared from both sides gives:

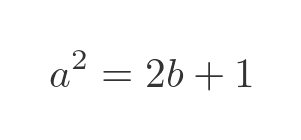
We can now solve for b:

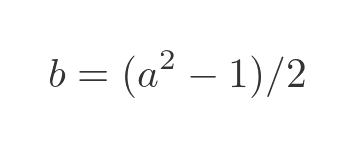
We need b to be a positive integer. This requires a squared to be an odd integer greater than 1. That will be true for any odd value of a that is 3 or more.

Having found b we can easily find c, because it is one more than b:

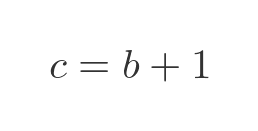
This tells us that for any odd value of a of 3 or more, we can create a Pythagorean triple using the formulas above. For example:

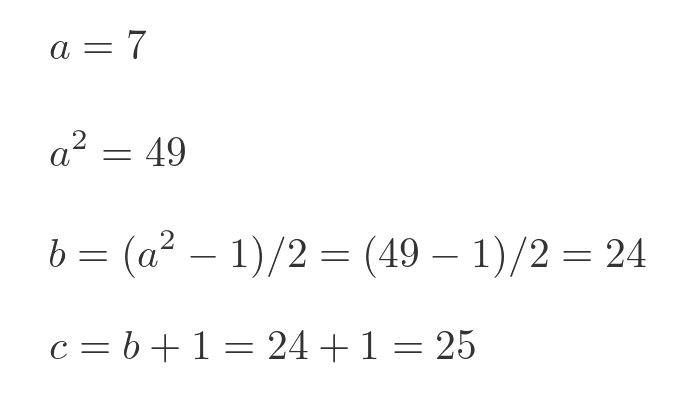
In this case, starting with an a value of 7 creates a (7, 24, 25) triple. Since there are infinitely many odd numbers, there are infinitely many triples that can be created using this method.

However, we set out to prove that there are infinitely many primary triples. How do we prove that these triples are all primary? We will prove this by contradiction - that is, we will assume a, b and c have a common factor other than 1, and show that this cannot be true.

1. If a, b and c to have a common factor f (where f is an integer of 2 or greater), then b and c must also have a common factor f.
2. If b and c have a common factor f, and c is greater than b, then c must equal b + nf where n is an integer of 1 or greater.
3. nf must be at least 2, because f is 2 or greater and n is 1 or greater.
4. Since c = b + 1 it is impossible for c to equal b + nf.

Since b and c cannot have a common factor other than 1, then a, b and c cannot have a common factor other than 1.

This proves that there are infinitely many primary triples of the form (a, b, b + 1).

Other primary Pythagorean triples

We have proven that there are infinitely many primary triples of the form (a, b, b + 1).

But there are other forms, for example (a, b, b + 2). Examples of this are:

• (8, 15, 17)
• (12, 35, 37)
• (16, 63, 65)
• (10, 99, 101)

It can be shown that there are infinitely many primary Pythagorean triples of this type too. And, of course, there are other types beyond that.

See also

• Pythagoras' theorem
• Pythagoras' theorem proof
• Einstein's proof of Pythagoras' theorem