Einstein's proof of Pythagoras' theorem

There are many proofs of Pythagoras' theorem, but perhaps one of the most elegant is Einstein's proof.

Here is a video on the topic:

The proof itself is quite simple, but there are a couple of important elements of the proof that are worth looking at first.

We don't need to draw squares to prove Pythagoras' theorem

For a right-angled triangle like this with sides a and b, and hypotenuse c, Pythagoras's theorem gives the result:

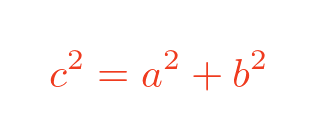
We often represent this by drawing squares on the 3 sides, like this:

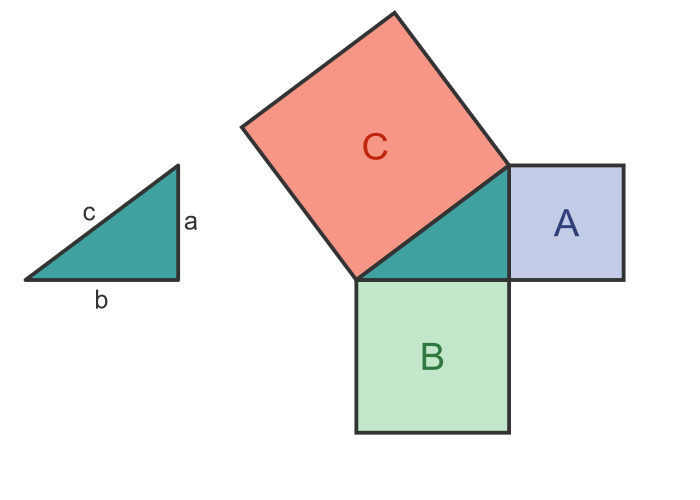
The area of square A is a². B is b² and C is c². So Pythagoras's theorem can be written as:

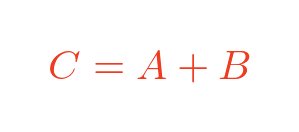
This means that if we can prove that the areas A and B add up to C, we have proved Pythagoras' theorem. Many proofs take this approach, using various clever methods to prove that the areas are equal.

However, this is a slight failure of imagination. Just because the formula contains the algebraic operation square doesn't mean we have to draw geometric squares to prove it!

We could use any shape. For example, we could draw a semicircle on each side of the triangle, instead of a square:

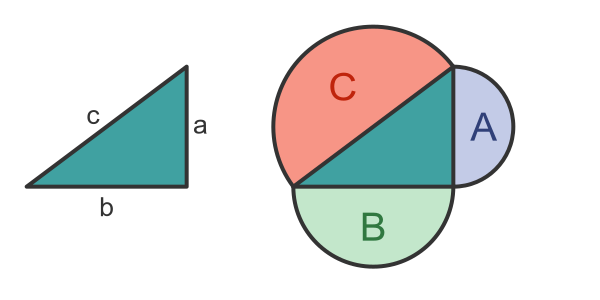
The area of semicircle A is:

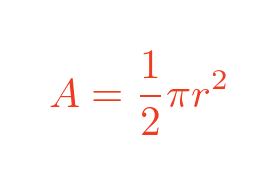
Where r is the radius of the semicircle. Since a is twice the radius, this gives:

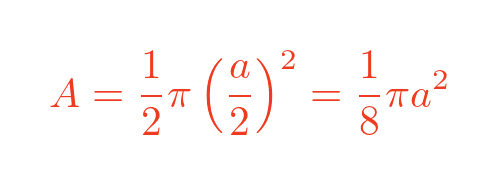
There are corresponding formulas to find B in terms of b, and C in terms of c. So, if areas A and B add up to C, we have:

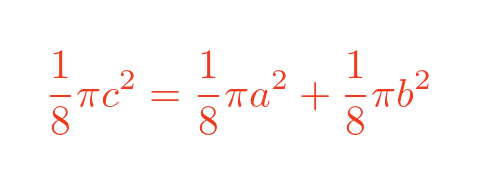
This is just Pythagoras' equation multiplied by a constant factor.

This means that if we can prove that the A and B add up to C, we have proved Pythagoras' theorem.

Now unfortunately there doesn't appear to be any simple way to prove that the semicircles obey this formula. But that wasn't the point. We have demonstrated that we can use any shape, not just a square. The requirement is that:

• The three shapes A, B and C are similar triangles. Similar means that they are the same shape but might be different sizes.
• The linear sizes of the three shapes are proportionate to the lengths of sides a, b and c.

Using semicircles wasn't any help, but we will see that using a special type of triangle leads to Einstein's elegant proof.

The altitude of a right-angled triangle creates three similar triangles

Let's construct a perpendicular line from the hypotenuse of the original triangle to its apex (this line is called the altitude of the triangle):

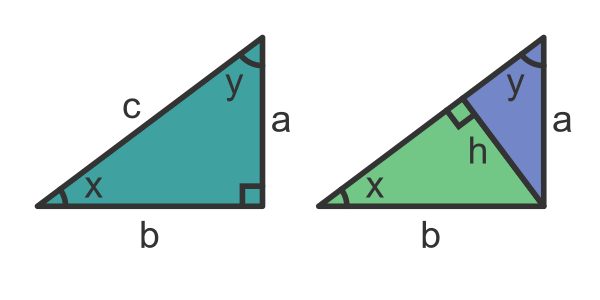
These two new triangles are both similar to the original triangle:

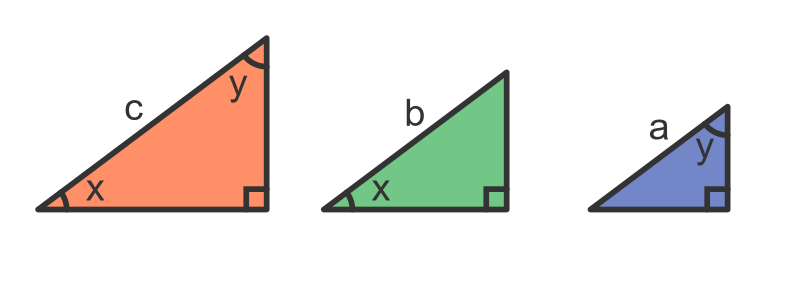
How do we know they are similar? Well, if two triangles have two angles the same, they are similar (and the third angle must also be the same). This means that triangles c and b above are similar because they both have a right angle and an angle x. This also means that the unmarked angle in b must be y, the same as triangle c.

Also, triangles c and a are similar because they both have a right angle and an angle y.

Notice that not only are the triangles similar, but the hypotenuses have lengths c, b, and a. So the three triangles have linear dimensions that are proportionate to the lengths of the sides of the original triangle.

Einstein's proof

We can now add these three triangles to the sides of the original triangle:

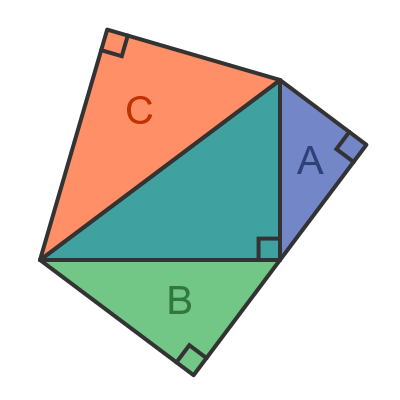
Triangle C is identical to the original triangle.

Since A and B are formed by dissecting the main triangle, this proves that:

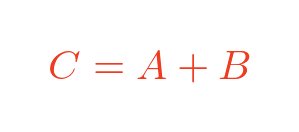
Which proves Pythagoras' theorem.

See also

• Pythagoras' theorem
• Pythagorean triples
• Pythagoras' theorem proof