Distance between two points on a graph
Categories: gcse trigonometry pythagoras
Level:

It is sometimes useful to find the distance between two points on a graph. For example, we might need to find the distance between the points A and B on this graph:
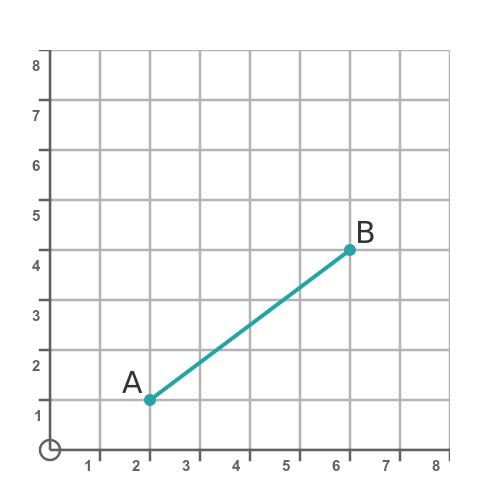
We can find the distance between the two points using the coordinates of the points. A is at (2, 1) and B is at (6, 4). In this article, we will use Pythagoras' theorem to find the length.
Finding lengths, angles and areas using coordinates is called coordinate geometry.
Horizontal and vertical distances
Before looking at the general case, we will take a look at a couple of simpler cases, shown here:
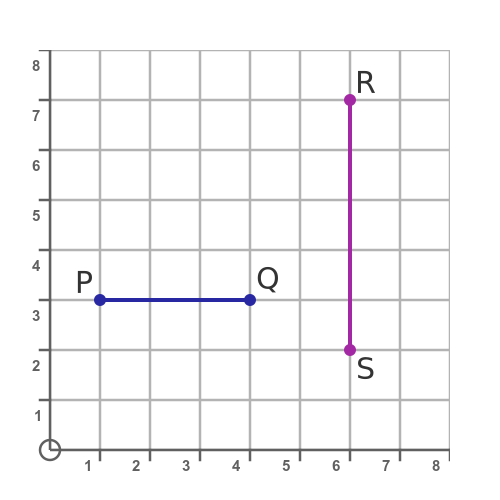
First, we will find the distance from P to Q. P is at (1, 3) and Q is at (4, 3). The line PQ is horizontal, because the two points P and Q have the same y value. The distance between P and Q is the horizontal distance, and it can be found by subtracting the x value of P from the x value of Q:
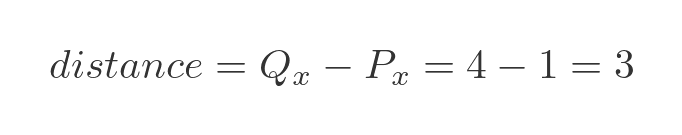
Next, we will find the distance from R to S. R is at (6, 7) and S is at (6, 2). The line RS is vertical because the two points R and S have the same x value. The distance between R and S is the vertical distance, and it can be found by subtracting the y value of R from the y value of S:
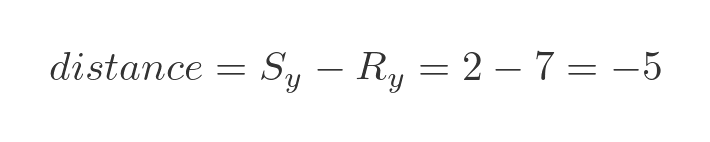
Notice that this gives a negative distance. That is because R is above S so we have to move in the negative y direction to get from R to S.
When we talk about the distance between two points, we don't usually care about the direction. For example, the distance between London and Edinburgh is 332 miles, and the distance between Edinburgh and London is also 332 miles. We don't say that one of those distances is minus 332 miles!
So we would normally ignore the sign and say that the distance between R and S is 5. We will see another explanation for this in the next section.
Diagonal distances
In this case, the line AB is neither horizontal nor vertical:
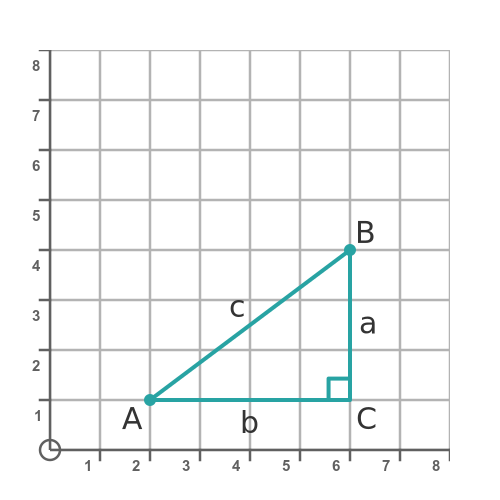
If we draw a straight line between A and B, that line has length c. That is the distance between A and B. How can we find the distance? Well, we can construct a right-angled triangle, and use Pythagoras' theorem.
Point C is horizontally in line with A and vertically in line with B. So we can find the coordinates of C, because it has the same y coordinate as A and the same x coordinate as B:
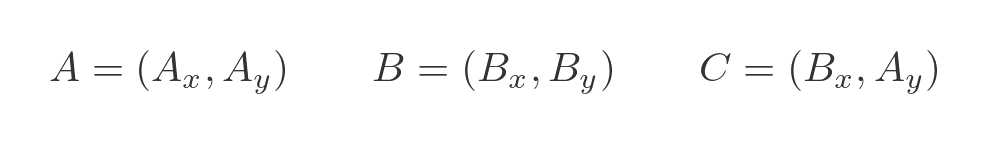
We cannot find c directly, but we can find:
- a (the vertical distance between B and C), which is the y component of C minus the y component of B.
- and b (the horizontal distance between A and C), which is the x component of C minus the x component of A.
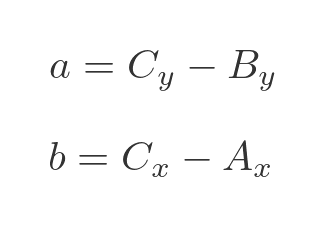
Since ABC forms a right-angled triangle, and we know a and b, we can find c using Pythagoras' theorem, which tells us that:
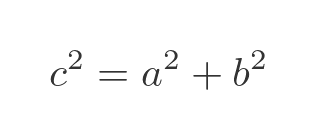
We can solve for c like this:
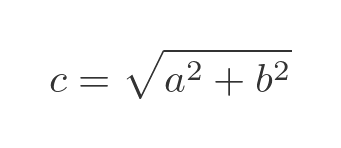
The values of a and b can be either positive or negative, depending on the locations of A and B. For example, in this case, b will be positive (because C is to the right of A) but a will be negative (because C is below B).
But remember that the Pythagoras formula uses the squares of a and b, and we know that the square of a number is always positive, even if the number itself is negative. So it makes no difference whether a and b are positive or negative, the result will still be the same.
Horizontal and vertical distances are special cases
We can apply the Pythagoras method to horizontal and vertical lines, and we will see that they are just special cases of the general case. Here is the diagram again with the line lengths labelled:

The line PQ can be thought of as a "triangle" with a width b but a height of zero. We can find b as before:
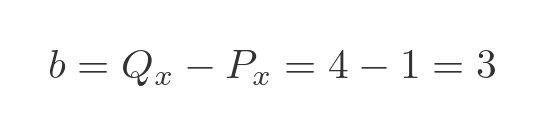
We can find the distance between the points using Pythagoras, but with a set to zero:
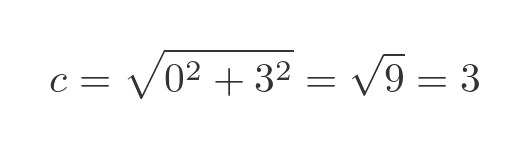
As we expect, the distance c is equal to 3. But c will always be positive even for a negative b.
The line RS can also be thought of as a "triangle", but this time with height a but a width of zero. We can find a as before:
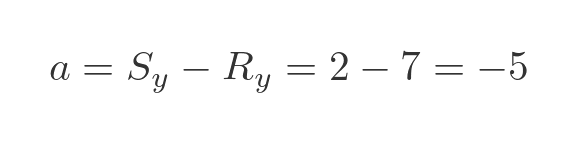
Again, we use Pythagoras, but with b set to zero:
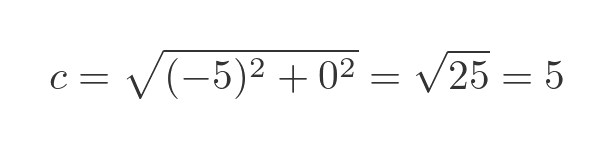
So now, even though a was negative, the distance between the points, c, is positive.
Example 1
As an example, we will find the length of the line AB from the triangle example above:

The points on the triangle are:

We can calculate a and b:
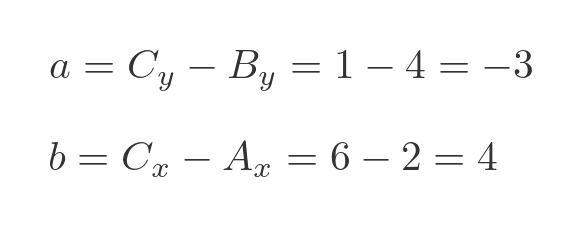
The value of a is negative, but as we saw earlier that does not matter as we will be squaring it anyway. We use Pythagoras to find c squared:
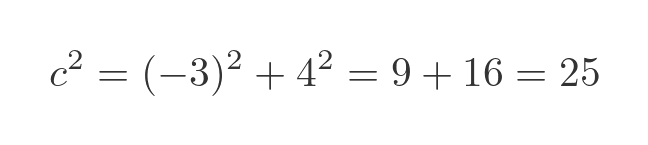
We find c by taking the square root:
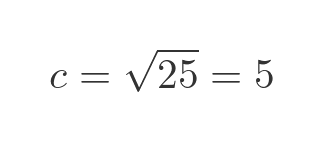
So the distance between A and B is 5. This is a 3-4-5 Pythagorean triple.
Example 2
In this next example, we will find the length of the line DE below:
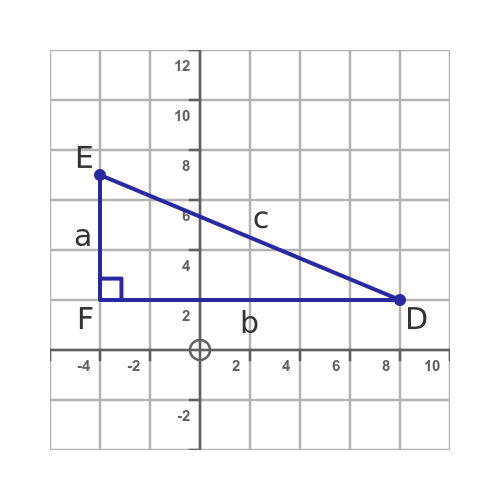
The points on the triangle are:
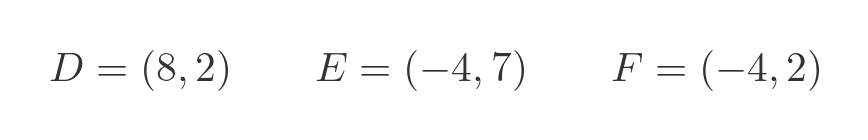
The difference in this case is that the points E and F are on the negative side of the y axis. That is no problem, but we need to be consistent with the signs:
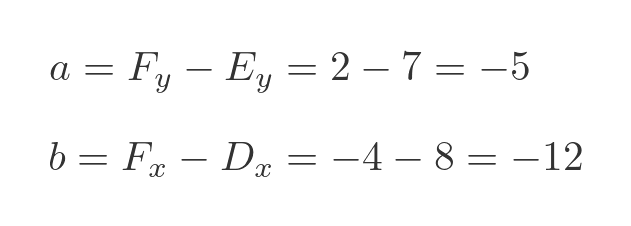
Pay particular attention to the way b is calculated. The x component of F is negative (-4) and the x component of D is positive (8), so to find b we calculate (-4) - 8 which is -12.
So this time a and b are both negative, but again the squares are both positive. We use Pythagoras to find c:
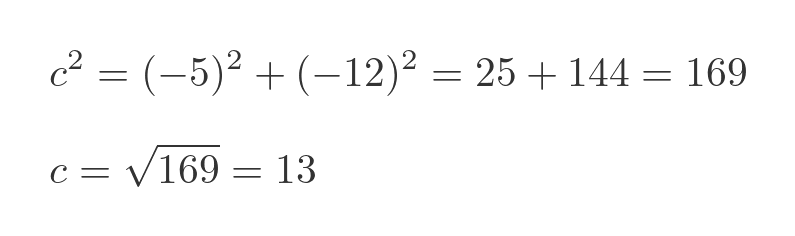
So the distance between D and E is 13. This is a 5-12-13 Pythagorean triple.
Example 3
Sometimes the question will just show the points, not the entire triangle. In this final example, we will find the length of the line UV below:
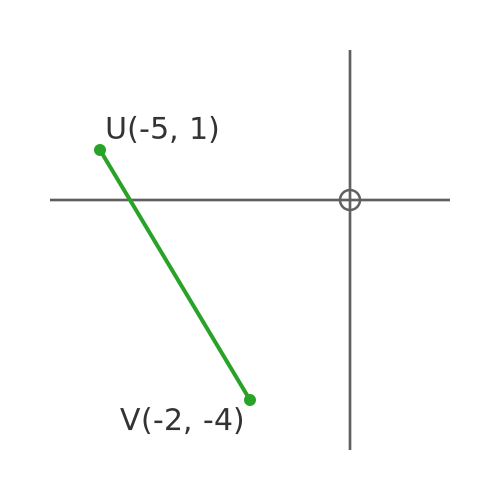
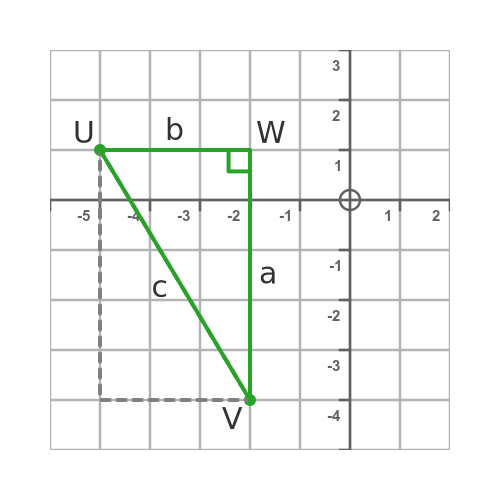
We need to redraw the points, on axes, showing the third point (which we will call W):
The points on the triangle are:
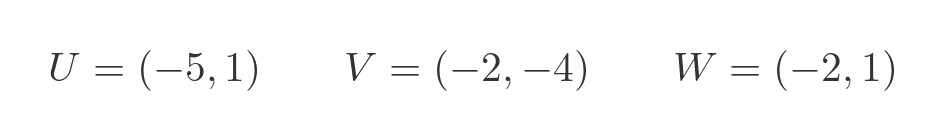
We have drawn the point W so that it is horizontally in line with U and vertically in line with V.
We could have drawn the point W so that it was horizontally in line with V and vertically in line with U. The point would then have been at (-5, -4). This would have created the triangle shown with the dashed grey line. It doesn't matter which one we choose, the triangle is still the same size and shape so the result for the length c would be the same.
As before, we need to be consistent with the signs when we do the calculation. Here are the values of a and b

We use Pythagoras to find c:
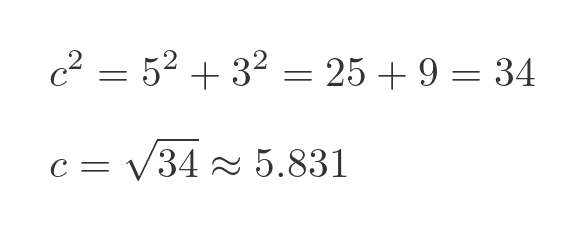
This time the triangle is not a Pythagorean triple, so the length can only be expressed exactly as a surd. The distance between U and V to 3 decimal places is 5.831.
Related articles
Join the GraphicMaths Newsletter
Sign up using this form to receive an email when new content is added to the graphpicmaths or pythoninformer websites:

Popular tags
adder adjacency matrix alu and gate angle answers area argand diagram binary maths cardioid cartesian equation chain rule chord circle cofactor combinations complex modulus complex numbers complex polygon complex power complex root cosh cosine cosine rule countable cpu cube decagon demorgans law derivative determinant diagonal directrix dodecagon e eigenvalue eigenvector ellipse equilateral triangle erf function euclid euler eulers formula eulers identity exercises exponent exponential exterior angle first principles flip-flop focus gabriels horn galileo gamma function gaussian distribution gradient graph hendecagon heptagon heron hexagon hilbert horizontal hyperbola hyperbolic function hyperbolic functions infinity integration integration by parts integration by substitution interior angle inverse function inverse hyperbolic function inverse matrix irrational irrational number irregular polygon isomorphic graph isosceles trapezium isosceles triangle kite koch curve l system lhopitals rule limit line integral locus logarithm maclaurin series major axis matrix matrix algebra mean minor axis n choose r nand gate net newton raphson method nonagon nor gate normal normal distribution not gate octagon or gate parabola parallelogram parametric equation pentagon perimeter permutation matrix permutations pi pi function polar coordinates polynomial power probability probability distribution product rule proof pythagoras proof quadrilateral questions quotient rule radians radius rectangle regular polygon rhombus root sech segment set set-reset flip-flop simpsons rule sine sine rule sinh slope sloping lines solving equations solving triangles square square root squeeze theorem standard curves standard deviation star polygon statistics straight line graphs surface of revolution symmetry tangent tanh transformation transformations translation trapezium triangle turtle graphics uncountable variance vertical volume volume of revolution xnor gate xor gate
