Binary addition, subtraction and negative numbers

In this article, we will see how to add and subtract 2 binary numbers. We will also see how we can represent negative numbers in binary.

Adding binary digits

We know how to add 2 denary digits, it is basic arithmetic, but here we will compare it to binary maths. Denary (aka decimal or base 10) digits can have values 0 to 9, and we add them like this:

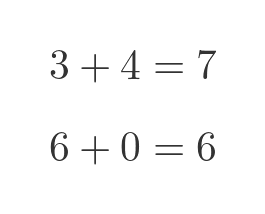
In binary (base 2) we only use the digits 0 and 1, and addition works like this:

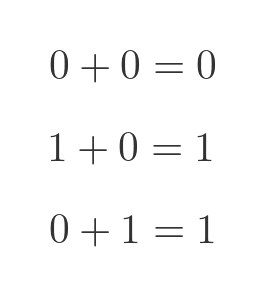
Adding with carry

In denary, if the two digits add up to more than 9, we have to carry one over to the next column:

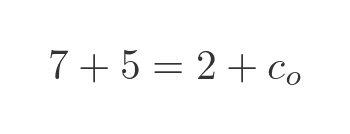
Here the answer is 12, of course, so the current column is set to 2 and we carry 1 over to the next column.

In binary, we have the same situation if we add 1 and 1. The result is binary 10 (2 in denary) which is 0 carry 1:

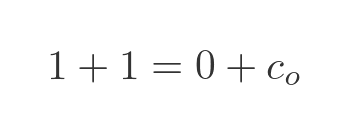
When we add the next columns, we must add 1 extra because it is carried in. In denary, it works like this:

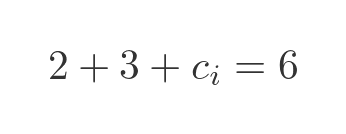
In binary, it works like this:

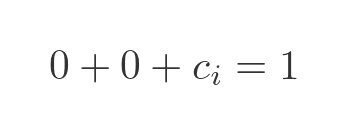
Finally, we have a situation where we have a carry in and a carry out. Here is an example in denary:

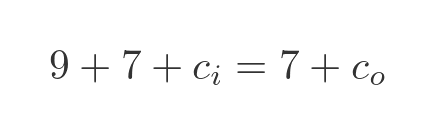
Here is an example in binary:

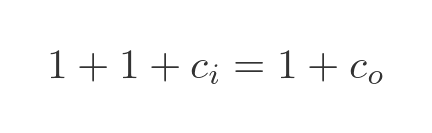
Binary addition truth table

The really useful thing about binary addition, and one of the reasons computers use binary, is that the rules of addition can be written as a simple truth table:

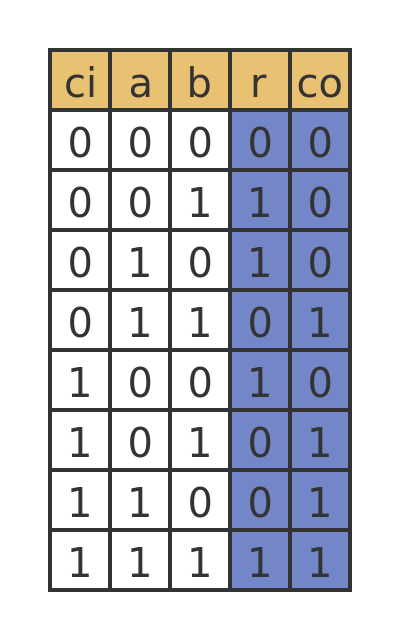
There are 3 inputs - the values to be added a and b, and the input carry, ci. This means there are 8 possible combinations of inputs, as shown in the table. There are 2 outputs, the result r and the output carry co.

This adder can be implemented using a few logic gates.

If we built a computer that used denary, a one-digit adder would have 200 input combinations (input a from 0 to 9, input b from 0 to 9, and ci of either 0 or 1). And the logic for combining those inputs would be far more complex.

Adding binary numbers

We have seen how to add binary digits, now let's look at how to add 2 entire binary numbers.

We will add the numbers a = 0111 and b = 0110:

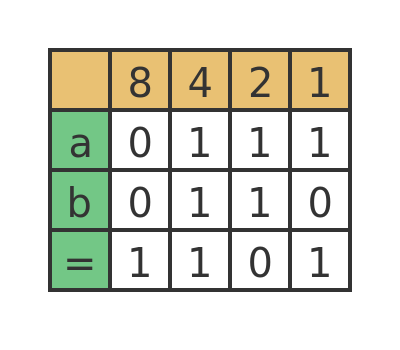
Looking at the 1s column first, we have 1 + 0, which gives 1 with no carry.

For the 2s column, we have 1 + 1, which gives 0, with 1 carried over.

In the 4s column we have 1 + 1 plus the 1 carried over from the 2s column. This gives 1 with 1 carried over.

Finally, in the 8s column we have 0 + 0 plus the 1 carried over from the 4s column. This gives 1 with no carry.

So the final result is 1101. As denary numbers, a is 7, b is 6, and the sum is 13.

Overflow

In a computer, the hardware that performs addition (the Arithmetic and Logic Unit, or ALU) usually has a fixed number of digits. This will often be 64 or 128 or some other power of 2. We refer to this as the number of bits the ALU supports.

To keep things simple, we will take the case of a computer with a 4-bit ALU. The first general microprocessor chip, released in 1971, was 4-bit, but it is extremely rare to use 4-bit chips these days. There are still some computers that use 8 bits (mainly computers that are "embedded" in household appliances or other devices) but most general purpose computers use more.

We are only using 4-bits here as a simple example. Just always remember that in a modern computer the ALU will be using more than 4 bits but will still work in a similar way.

The binary addition we performed above used 4-bits. A 4-bit binary number can hold any value between 0 and 15 (denary). An interesting question is, what happens if we add the denary values 7 and 10? Here is the result:

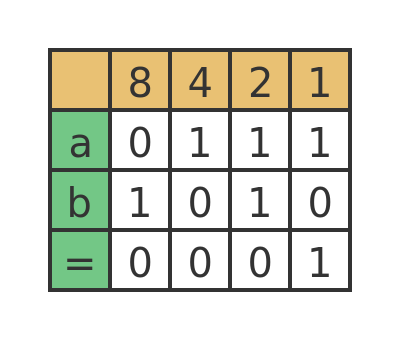
In the 1s column, 1 + 0 is 1. In the 2s column, 1 + 1 is 0 carry 1. In the 4s column 1 + 0 plus the 1 carried over is 0 carry 1. And in the 8s column, 0 + 1 plus the 1 carried over is 0 carry 1.

So the result is binary 0001.

What has happened here is the value has overflowed the 4 bits available. Denary values 7 and 10 add up to 17, which is 10001 in binary. But we can only store 4 bits, so the extra 1 "falls off" the end, leaving just 0001.

The ALU can detect that this has happened, because there was a 1 carried over when we added the 8s column. So the ALU knows there has been an overflow, but it doesn't automatically treat it as an error, because it can be rather useful, as we will see.

Visualising overflow

If you think of how a clock works, the hours count from 1 to 12, then start again at 1. The hour hand goes round and round.

We can visualise a 4-bit binary value in the same way. It goes from 0 to 15 then starts at 0 again. So let's draw it as a clock face:

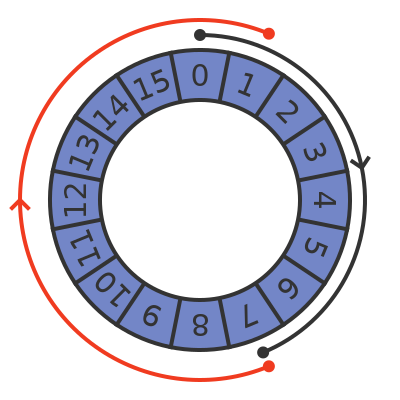
This diagram shows the previous case, 7 + 10. The black arrow has an arc length equivalent to 7 units. The red arrow has an arc length of 10 units. Starting from 0, if we add 7 units and then 10 units, we wrap around and end up at value 1, exactly as we saw previously.

In this case, of course, that would be an error. 7 + 10 definitely isn't 1. Many programming languages use fixed-size integers, and potential overflow is something that needs to be considered when choosing the size of integer to use. Typical integer sizes are 8-bit (maximum value 255 in denary), 16-bit (maximum value 65535), 32-bit (values up to about 4 billion), and 64-bit (very large values). It is generally the programmer's job to ensure that the type of integer used is large enough to avoid overflow problems.

Subtraction

We know how to add binary numbers, but how do we subtract them? It is very easy, using what we have just learned about binary overflow.

This diagram shows 6 - 4:

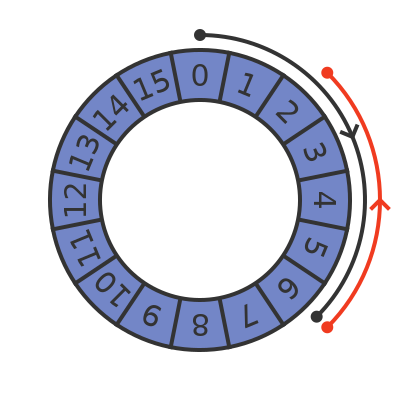
To subtract, we start at position 0 and move clockwise by 6. We then move counterclockwise by 4 to perform the subtraction. This gives the result 2.

But as we saw previously, it is also possible to perform subtraction by adding a number that is large enough to cause an overflow:

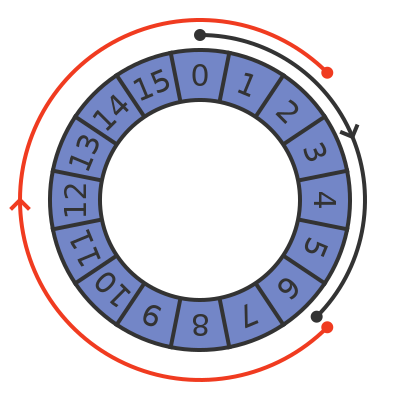
Here we have added 12 instead of subtracting 4, to give exactly the same result. This allows the processor chip to use the adder to perform subtraction, which was an important consideration in the early days of modern computing when the technology only allowed a limited number of gates on a CPU chip. But more importantly, it provided a way to represent negative numbers, as we will see in a moment.

So we can subtract 4 by adding 12. But why 12? Well, that is because 4 + 12 adds up to 16. Rotating by 4 and then 12 amounts to a full turn that gets us back where we started. So rotating by 12 is 4 less than a full turn. This means that rotating by 12 CW is equivalent to rotating by 4 CCW.

In general, to subtract n we simply need to add 16 - n.

The only problem here, of course, is that we are trying to use addition to perform subtraction. But we need to perform a subtraction to find the number we need to add!

Fortunately, there is a simple way to find 16 - n. Here is the number 4 in binary (using 4 bits):

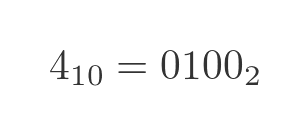
Now we invert this number:

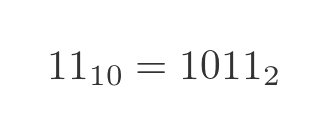
We call the inverted number the 1s complement of the original. The 1s complement of 4 happens to be 11 denary. But the important thing is, when we add these two numbers we get all 1s in binary:

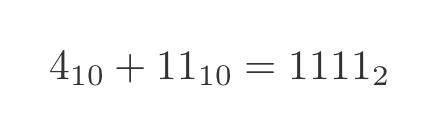
This will always be the case because whatever number we start with, the inverse will have a 0 wherever the original had a 1, and a 1 wherever the original had a 0. So every binary place will be adding 0 + 1 (or 1 + 0) which adds to 1 with no carry. So the result has a 1 in every binary place.

If we add a 1 to this result, the entire binary number will be 0s, with 1 carried over (that drops off the end of the fixed length binary number):

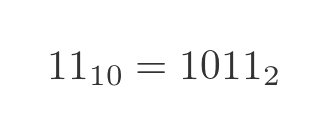
Subtraction algorithm

In summary, to calculate x - y in binary, we must:

• Find the 1s complement (y1) of y by inverting every bit.
• Find the 2s complement (y2) of y by adding 1 to the 1s complement, y1.
• x - y is equal to x + y2.

One thing to remember is that the binary numbers we are using are always positive. This means that y must be less than x, otherwise the result will be incorrect.

It is also worth noticing that, when we perform a subtraction, we expect the addition to overflow, because that indicates the addition has wrapped around.

Negative numbers

It is possible to represent negative numbers in binary.

We already know that adding 15 has the same effect as subtracting 1. And adding 14 has the same effect as subtracting 2. So we could just say that 15 represents -1, 14 represents -1, and so on. This gives us a new number wheel:

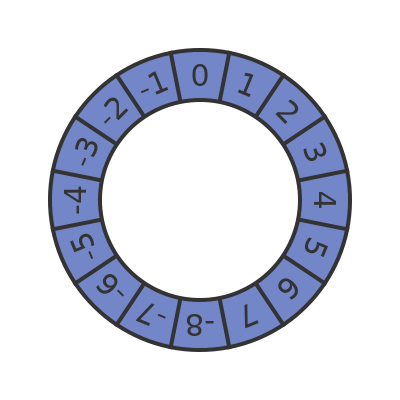
This system allows us to represent positive and negative numbers. It is also consistent, for example here is what happens if we add -3 to 5:

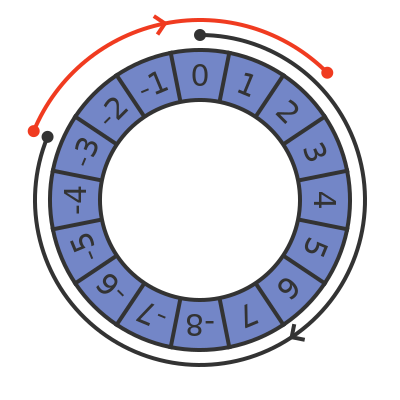
We move round by 13 places to get to -3, then move round another 5 places to add 5. The result is 3.

Here is what happens if we add -2 to -4:

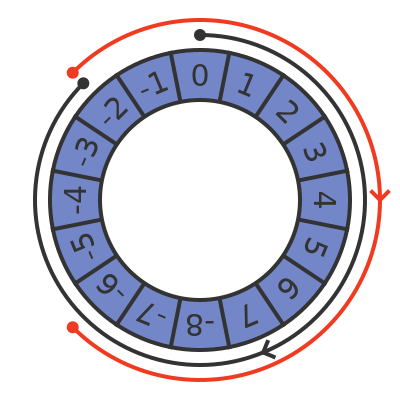
We move round 14 places to get to -2, then 12 more to add -6. The result is -6.

Signed and unsigned numbers

We have seen two different versions of the binary number wheel:

• In the first version, positions 0 to 15 represent values 0 to 15. We say this is an unsigned integer.
• In the other version, positions 0 to 7 represent values 0 to 7, but positions 8 to 15 represent values -8 to -1. We say this is a signed integer.

So which should we use?

The fact is computers can, and do, use both. Many programming languages allow you to declare variables that use either signed or unsigned values.

The important thing is, within any given calculation, you must decide which one you are using, and stick to just that one interpretation.

If you need to use negative numbers, you must use signed numbers.

If your numbers are always positive, you can use either use signed or unsigned numbers. The advantage of unsigned numbers is that they give a greater range (the largest positive signed 4-bit number is 7, whereas the largest positive unsigned 4-bit number is 15).

The sign bit

Looking at the signed numbers we see that the positive numbers run from 1 to 7, but the negative numbers run from -1 to -8. Why is that?

Well first, of course, 0 is neither positive nor negative. So that leaves an odd number of other values, so the positive and negative counts can't be the same.

Why do the negative numbers get an extra value? To understand that we need to look at the binary values. Numbers 1 to 7 have binary values 0001 to 0111. Numbers -1 to -8 have values 1111 to 1000 (counting backwards).

So this arrangement means that all the negative values have the most significant bit set to 1, and all the positive or 0 values have the most significant bit set to 0. This gives us a very easy way to see if a number is negative or not.

We call the most significant bit the sign bit.

See also

• Binary numbers